MATLAB仿真技术速成：10大方法让你快速掌握模拟艺术

# 1. MATLAB仿真技术概述

MATLAB（Matrix Laboratory的缩写）是一种高性能的数值计算和可视化软件，广泛应用于工程计算、控制设计、信号处理和通信领域等。它提供了强大的数值分析、矩阵运算、信号处理和图形展示等功能，尤其在仿真技术方面，凭借其简洁的语法、丰富的工具箱和强大的图形处理能力，成为了科研和工程仿真领域的首选工具。

仿真，从本质上讲，是使用模型来模拟现实世界中的系统和过程。在工程应用中，仿真可以用来测试和验证理论和设计，而不必在实际系统上进行昂贵或危险的操作。MATLAB的仿真技术，特别是在控制系统、信号处理、机器学习等多个领域，已经得到了广泛认可和应用。

在开始深入学习MATLAB仿真技术之前，我们首先需要对其有一个基本的了解，包括MATLAB的发展历史、仿真技术的基本概念，以及MATLAB在各行各业中的应用案例。这将为我们后续章节中详细讲解的仿真环境搭建、操作指南、工具箱资源介绍，乃至具体仿真方法和实战演练打下坚实的基础。

# 2. MATLAB仿真环境搭建与基础操作

### 2.1 MATLAB软件安装与配置

#### 2.1.1 软件的安装步骤

安装MATLAB软件是进行仿真的第一步。确保你的计算机满足软件的系统要求后，可以按照以下步骤安装MATLAB：

1. 下载MATLAB安装包：前往MathWorks官网下载适合你的操作系统版本的MATLAB安装包。
2. 运行安装程序：双击下载的安装包，开始安装向导。
3. 接受许可协议：阅读并同意MATLAB的许可协议。
4. 选择安装路径：选择一个包含足够存储空间的文件夹作为安装目录。
5. 安装选项：根据个人需求选择要安装的工具箱和功能。
6. 启动安装过程：点击安装按钮开始安装，等待安装完成。

#### 2.1.2 环境变量与路径设置

安装完成后，配置MATLAB的环境变量和路径是关键的一步，这可以保证MATLAB能够正确地运行和调用工具箱。

1. 环境变量设置：在Windows系统中，通过“系统属性”->“高级”->“环境变量”来设置`PATH`变量，添加MATLAB的安装路径和其`bin`目录。
2. MATLAB路径配置：在MATLAB命令窗口中，使用`addpath`命令来添加额外的路径。比如：`addpath('C:\myToolboxes')`。

### 2.2 MATLAB基本操作指南

#### 2.2.1 命令窗口使用技巧

命令窗口是MATLAB中最基本的操作界面。在命令窗口中输入命令并按回车键，可以立即看到结果。这里有一些操作技巧：

1. 使用上下箭头键可以回顾之前输入的命令。
2. 使用`Tab`键自动补全命令或变量名。
3. 通过`Ctrl+C`取消当前正在执行的命令。
4. 使用`clc`清除命令窗口的内容。

#### 2.2.2 脚本与函数的基本编写

MATLAB的脚本和函数是实现复杂算法和自动化任务的重要工具。编写脚本和函数需要注意以下几点：

1. 脚本使用`.m`作为文件扩展名，可以直接运行，不需要输入函数名和参数。
2. 函数也需要以`.m`为扩展名，但需要定义函数头，如`function y = myFunction(x)`，其中`y`是返回值，`x`是输入参数。
3. 在编写代码时，可以使用MATLAB内置的函数和操作符，如矩阵操作、逻辑判断等。
4. 要保存和运行脚本或函数，可以点击MATLAB编辑器的“保存”按钮，并通过命令窗口或者通过点击编辑器中的绿色三角形运行。

function y = addTwoNumbers(a, b)
    y = a + b; % 将两个数相加的结果赋值给y
end

### 2.3 MATLAB工具箱与资源介绍

#### 2.3.1 核心工具箱的功能与应用

MATLAB的核心工具箱提供了丰富的功能用于数学计算、数据分析和可视化等。这些工具箱包括：

1. **MATLAB Core**：提供基本的数学计算功能。
2. **Simulink**：用于多域仿真和基于模型的设计。
3. **Signal Processing Toolbox**：支持信号处理、分析和滤波器设计等。
4. **Image Processing Toolbox**：提供图像处理和分析的功能。

每个工具箱都有相应的函数和用户界面来执行特定的任务。

#### 2.3.2 在线资源和社区支持

MathWorks提供了大量的在线资源，包括：

1. **MATLAB Central**：是用户交流和分享代码、问题解答的社区。
2. **Documentation & Learning**：提供官方文档和学习材料。
3. **File Exchange**：用户可以下载其他用户贡献的工具箱和脚本。

这些资源为MATLAB用户提供了一个学习和解决问题的平台。

在本章节中，我们详细介绍了MATLAB的安装配置、基本操作以及工具箱和资源。随着对MATLAB的进一步学习和使用，你会发现它不仅仅是一个仿真工具，还是一个功能强大的编程和数据分析平台。下一章节，我们将深入探索MATLAB在基本仿真方法上的应用。

# 3. MATLAB基本仿真方法与实例

## 3.1 数值计算与数据可视化

### 3.1.1 矩阵操作与数值分析

MATLAB是一种高级的数值计算环境，其核心是以矩阵为基础的数据结构。因此，掌握MATLAB的矩阵操作对于进行数值分析至关重要。矩阵在MATLAB中不仅仅局限于二维数组，它还支持更高维度的数组操作，这为复杂系统的分析提供了便利。

在进行矩阵操作时，基本的加减乘除运算符`+`, `-`, `*`, `/`可以直接应用于矩阵，但需要注意的是，这些运算符在MATLAB中具有矩阵运算的特性，而非传统意义上的标量运算。例如，在MATLAB中，两个矩阵的乘法要求矩阵的内维数相匹配，而矩阵的除法则是通过求逆矩阵实现的。

此外，MATLAB提供了一系列函数来执行更复杂的矩阵操作，如：
- `eig`计算矩阵的特征值和特征向量。
- `svd`计算矩阵的奇异值分解。
- `inv`计算矩阵的逆。

一个典型的数值计算过程可能包括矩阵的创建、矩阵运算以及数值解的求解等步骤，如下代码展示了如何使用MATLAB进行基本的矩阵操作和求解线性方程组。

A = [3, 2, -1; 2, -2, 4; -1, 0.5, -1];
b = [1; -2; 0];
x = A\b; % 使用左除运算符求解线性方程组Ax=b
disp(x); % 显示结果

在上述代码中，我们首先定义了矩阵`A`和向量`b`，然后使用左除运算符`\`来求解线性方程组`Ax=b`。此操作在背后实际调用了MATLAB内置的求解器，例如`lu`分解或者`qr`分解。

矩阵操作和数值分析是数据处理的基础，也是仿真的重要组成部分。通过熟悉和掌握这些基础操作，可以为进一步的数值分析和仿真提供坚实的基础。

### 3.1.2 二维和三维数据绘图

数据可视化是仿真领域中的一个重要方面，它可以帮助我们直观地理解数据和结果。MATLAB提供了强大的二维和三维绘图功能，通过这些功能，用户可以轻松创建复杂的图表和图形。

为了进行数据可视化，MATLAB提供了一些常用的绘图函数，如`plot`、`bar`、`histogram`、`scatter`等，用于创建二维图表。当需要创建三维图形时，可以使用`plot3`、`mesh`、`surf`等函数。

下面展示了一个简单的二维图表创建示例：

x = linspace(0, 2*pi, 100); % 生成0到2π的100个线性间隔点
y = sin(x); % 计算对应的正弦值
plot(x, y); % 绘制y关于x的函数图像
title('Simple Plot of sin(x)');
xlabel('x');
ylabel('sin(x)');

而在三维绘图方面，MATLAB同样提供了丰富的工具。例如，以下代码段展示了如何创建三维曲面图：

[X, Y] = meshgrid(-5:0.2:5, -5:0.2:5); % 创建X和Y坐标网格
Z = sin(sqrt(X.^2 + Y.^2)); % 计算Z坐标值
surf(X, Y, Z); % 绘制三维曲面图
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
title('3D Surface Plot');

通过这些绘图函数，可以将数据结果转换为视觉图形，帮助研究者更好地理解数据，发现数据中的趋势和模式。同时，在仿真领域，图形化结果也有助于向非专业听众展示复杂概念和数据。

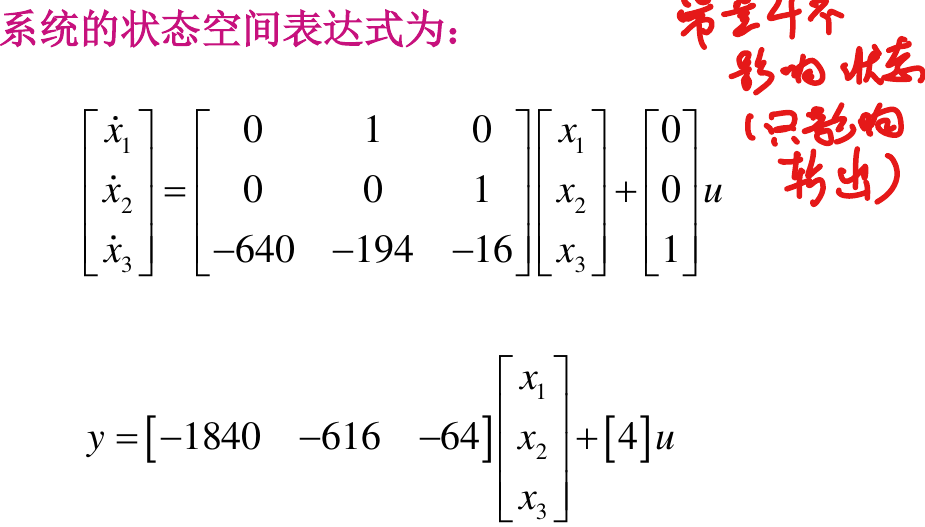
### 3.2 动态系统的模拟与分析

动态系统的建模与分析是MATLAB仿真中的一个重要主题，它涉及到对系统的动态行为进行数学描述和计算机仿真。动态系统可以是连续的也可以是离散的，它们都可以通过差分方程或微分方程来描述。

#### 3.2.1 离散和连续系统的建模

离散系统通常用差分方程来描述，它们的动态行为是在一系列离散的时刻点上定义的。例如，可以使用Z变换来分析离散时间信号和系统。

下