算法设计中的顺序存储：空间复杂度优化实战指南


# 摘要
本文深入探讨了顺序存储及空间复杂度相关的概念，并详细分析了基础与高级数据结构的空间优化方法。通过系统地阐述空间复杂度的定义、计算方法以及优化原理，为读者提供了理论和实践相结合的空间优化策略。文章还涵盖了算法设计中排序、搜索、动态规划等算法的空间优化技术，并展望了未来节省内存的新技术、优化工具的发展以及算法教育与研究的前沿领域。整体而言，本文旨在为开发人员提供一整套空间优化的指导方案，提升软件的性能与资源使用效率。

# 关键字
顺序存储；空间复杂度；数据结构优化；内存管理；算法设计；技术展望

参考资源链接：[顺序存储方式：行优先与列优先详解](https://wenku.csdn.net/doc/7o4cqp6nq0?spm=1055.2635.3001.10343)
# 1. 顺序存储概念解析

## 1.1 什么是顺序存储

在计算机科学中，顺序存储是一种数据存储方法，其中物理上连续的内存空间被用来存储逻辑上相邻的数据项。这种存储方式在数组中被广泛使用，因为它能够高效地通过索引直接访问元素。

## 1.2 顺序存储的优势

顺序存储的主要优势在于存取速度快，特别是在随机访问时，因为内存地址可以直接计算得出。此外，顺序存储对于某些算法来说能够提供更好的性能，尤其是在处理线性数据结构时。

## 1.3 顺序存储的局限性

尽管有上述优势，顺序存储也存在局限性。例如，动态数组的大小在初始化时必须确定，若需动态增长，则需要进行额外的内存操作。这些操作可能导致内存碎片，影响系统的性能。

## 1.4 顺序存储的使用场景

顺序存储常用于需要快速随机访问元素的场景，例如在实现缓存系统、高效的数据排序和搜索算法中。理解顺序存储的概念对于优化算法的空间复杂度至关重要。

# 2. 空间复杂度基础知识

## 2.1 空间复杂度的定义

空间复杂度是指在实现一个算法时，除了输入数据所占用的空间外，算法本身运行过程中临时占用存储空间的大小。它反映了算法对存储空间需求的增长趋势。

### 2.1.1 时间与空间的权衡

在计算机科学中，时间和空间是资源的两大组成部分，它们通常处于一种权衡关系中。一个算法如果在运行时间上表现得非常快，可能就会需要更多的内存来存储中间结果或辅助数据结构。反之，如果节省内存，可能就需要更复杂的逻辑来减少空间的使用，这样会增加算法的运行时间。

理解时间和空间的权衡对于编写高效的算法至关重要。对于一些内存敏感的应用，比如嵌入式系统或资源受限的环境，空间复杂度成为了一个重要考量。而在现代计算机系统中，由于内存相对充足，一些应用可能更侧重于时间效率。

### 2.1.2 空间复杂度的数学表示

空间复杂度通常用大O符号表示，如O(1), O(n), O(n^2)等。这表示算法的空间需求是输入大小的常数倍、线性倍或平方倍。例如：

- O(1): 常数空间复杂度。无论输入大小如何，算法使用的空间是固定的。
- O(n): 线性空间复杂度。算法所需空间与输入数据量线性相关。
- O(n^2): 多维空间复杂度。通常出现在需要二维数组或者多重循环的情况。

## 2.2 空间复杂度的计算方法

### 2.2.1 常数空间复杂度

常数空间复杂度指算法所需的空间不会随输入数据的规模增加而增加。例如，一个简单的加法函数，它接收两个整数参数，其空间复杂度为O(1)。

def add(a, b):
    return a + b

# 空间复杂度分析：O(1)，不需要额外空间

### 2.2.2 线性空间复杂度

线性空间复杂度意味着算法所需的空间与输入数据量成正比。例如，一个复制数组的函数，其空间复杂度为O(n)。

def copy_array(arr):
    new_arr = [0] * len(arr)
    for i in range(len(arr)):
        new_arr[i] = arr[i]
    return new_arr

# 空间复杂度分析：O(n)，需要一个大小为n的新数组

### 2.2.3 多维空间复杂度

多维空间复杂度出现在算法需要使用多维数组或嵌套数据结构时。例如，一个生成n x m矩阵的函数。

def create_matrix(n, m):
    matrix = [[0 for _ in range(m)] for _ in range(n)]
    return matrix

# 空间复杂度分析：O(n*m)，需要n*m的空间存储矩阵

## 2.3 空间复杂度的优化原理

### 2.3.1 重用内存的概念

重用内存是指尽量使用已经分配的内存空间，避免不必要的内存分配和释放。这可以通过局部变量重用、对象池等方式实现。

### 2.3.2 数据压缩技术

数据压缩技术可以在不丢失数据信息的前提下减少所需存储空间。这对于存储资源紧张或者需要传输大量数据的场景特别有用。

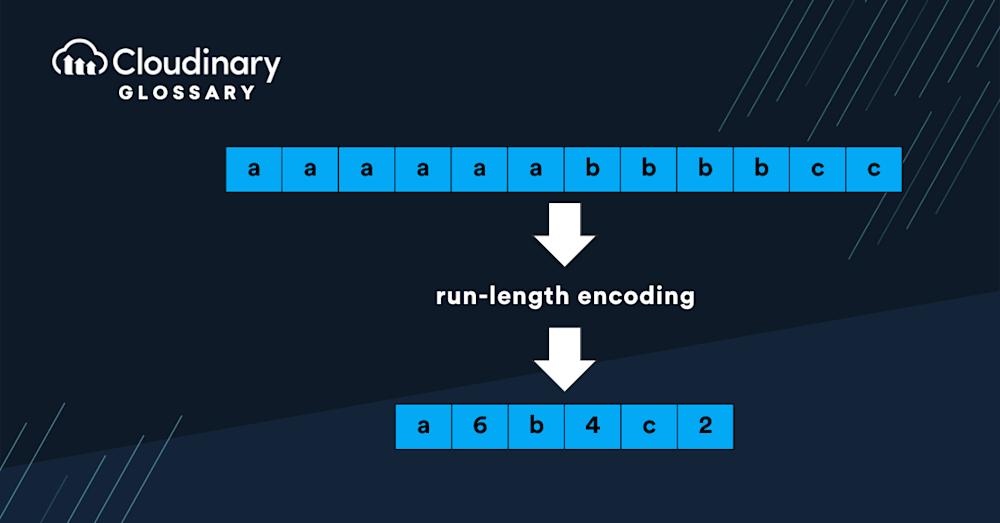
例如，可以使用字符计数编码、行程长度编码（RLE）、霍夫曼编码等方法进行数据压缩。这些技术可以减少存储空间的需求，但可能会增加数据解压的时间成本。

# 示例：一个简单的字符计数压缩函数
def compress_string(s):
    compressed = []
    count = 1
    for i in range(1, len(s)):
        if s[i] == s[i-1]:
            count += 1
        else:
            compressed.append(s[i-1] + (str(count) if count > 1 else ''))
            count = 1
    compressed.append(s[-1] + (str(count) if count > 1 else ''))
    return "".join(compressed)

# 空间复杂度分析：O(n)，输入字符串长度为n，压缩后的空间取决于字符的重复率

在这一章节中，我们探讨了空间复杂度的基础知识，包括其定义、计算方法和优化原理。下一章节将深入基础数据结构的空间优化。

# 3. 基础数据结构的空间优化

在实际应用中，数据结构的存储效率对于系统性能有着直接的影响。为了更好地理解如何优化空间，我们首先需要对基础数据结构的空间效率进行分析，并探讨如何在实际编程中进行优化。

## 3.1 数组和链表的选择与优化

数组和链表是编程中使用最频繁的两种数据结构。它们各自有着不同的空间效率特点，选择合适的数据结构对于优化空间至关重要。

### 3.1.1 数组的空间效率分析

数组是一种线性数据结构，它使用一段连续的内存空间来存储一系列相同类型的数据元素。数组的这种连续存储特性决定了它在空间上的效率。

- **空间连续性**：数组的元素存储在连续的内存地址中，这使得数组能够通过索引快速访问任何一个元素，时间复杂度为O(1)。
- **空间浪费**：由于数组的大小在初始化时就已经确定，因此如果数组没有完全被使用，那么未使用的空间就会造成浪费。

数组的空间优化策略通常涉及到动态数组（Dynamic Array），它能够在运行时动态地调整大小，以适应数据量的变化。

### 3.1.2 链表的空间效率分析

链表是一种线性数据结构，它由一系列节点组成，每个节点包含数据和指向下一个节点的指针（或引用）。

- **灵活性**：链表的节点可以在内存中任何位置，因此不会产生像数组那样的空间浪费问题。
- **空间开销**：每个链表节点除了存储数据外，还需要额外的空间来存储指针，这增加了额外的空间开销。

链表的空间优化通常需要减少节点的额外开销，例如，通过压缩节点结构来减少每个节点的大小。

### 3.1.3 实战：选择合适的数据结构

在实际应用中，根据具体需求来选择数组或链表是一个重要的决策。例如：

- 当需要快速的随机访问时，应该选择数组。
- 当插入或删除操作频繁时，链表通常是更好的选择。

下面是一个简单的代码示例，演示了在C++中如何使用数组和链表：

#include <iostream>
#include <vector>
#include <list>

int main() {
    // 数组（动态数组）示例
    std::vector<int> vec = {1, 2, 3, 4, 5}; // 动态数组
    vec.push_back(6); // 动态扩展空间

    // 链表示例
    std::list<int> lst = {1, 2, 3, 4, 5}; // 双向链表
    lst.push_back(6); // 添加元素到链表末尾

    // 输出数组和链表的元素
    for (int num : vec) std::cout << num << " ";
    std::cout << std::endl;

    for (int num : lst) std::cout << num << " ";
    std::cout << std::endl;

    return 0;
}

在上述代码中，`std::vector` 是C++标准库中的动态数组实现，而 `std::list` 是链表的实现。代码逻辑的逐行解读分析如下：

- 第5行：定义了一个 `std::vector<int>` 类型的动态数组 `vec`。
- 第6行：向 `vec` 中添加了一些初始值。
- 第7行：使用 `push_back` 方法向 `vec` 添加一个新的元素。
- 第9行：定义了一个 `std: