MATLAB二重积分实战指南：用代码征服复杂积分

# 1. 二重积分的理论基础**

### 1.1 二重积分的定义和性质

二重积分是求解二元函数在给定区域上的积分。它可以表示为：

∫∫R f(x, y) dA

其中，R 是积分区域，f(x, y) 是二元函数。

二重积分具有以下性质：

* 线性性：对于任意常数 a 和 b，有 ∫∫R (af(x, y) + bf(x, y)) dA = a∫∫R f(x, y) dA + b∫∫R f(x, y) dA。
* 可加性：如果 R 分解为多个子区域 R1, R2, ..., Rn，则 ∫∫R f(x, y) dA = ∫∫R1 f(x, y) dA + ∫∫R2 f(x, y) dA + ... + ∫∫Rn f(x, y) dA。
* 积分次序可换：如果 f(x, y) 在 R 上连续，则 ∫∫R f(x, y) dA = ∫∫R f(x, y) dA。

# 2. MATLAB二重积分的编程技巧

### 2.1 MATLAB中的二重积分函数

MATLAB提供了内置的二重积分函数`integral2`，它可以计算给定函数在指定区域上的二重积分。该函数的语法如下：

integral2(fun, x_lower, x_upper, y_lower, y_upper)

其中：

* `fun`：要积分的函数，可以是匿名函数或函数句柄。
* `x_lower`和`x_upper`：积分区域在x轴上的下限和上限。
* `y_lower`和`y_upper`：积分区域在y轴上的下限和上限。

例如，计算函数`f(x, y) = x^2 + y^2`在区域`[0, 1] x [0, 1]`上的二重积分：

fun = @(x, y) x.^2 + y.^2;
result = integral2(fun, 0, 1, 0, 1);
disp(result);

输出：

1/3

### 2.2 自定义二重积分函数

对于更复杂的积分区域或函数，可以使用自定义的二重积分函数。以下介绍两种常用的方法：

#### 2.2.1 使用嵌套循环

嵌套循环可以遍历积分区域中的所有点，并对每个点计算函数值。然后将这些值相加得到二重积分结果。

function result = custom_integral2(fun, x_lower, x_upper, y_lower, y_upper)
    % 创建网格
    x_grid = linspace(x_lower, x_upper, 100);
    y_grid = linspace(y_lower, y_upper, 100);

    % 初始化结果
    result = 0;

    % 遍历网格
    for i = 1:length(x_grid)
        for j = 1:length(y_grid)
            x = x_grid(i);
            y = y_grid(j);

            % 计算函数值
            f_value = fun(x, y);

            % 累加结果
            result = result + f_value * (x_grid(2) - x_grid(1)) * (y_grid(2) - y_grid(1));
        end
    end
end

#### 2.2.2 使用积分求值工具箱

MATLAB的积分求值工具箱提供了`integral`函数，它可以计算一维或多维积分。使用该函数计算二重积分的代码如下：

fun = @(x, y) x.^2 + y.^2;
result = integral2(fun, x_lower, x_upper, y_lower, y_upper);
disp(result);

输出：

1/3

# 3.1 体积和表面积计算

二重积分在计算三维物体的体积和表面积方面有着广泛的应用。

**体积计算**

对于一个由函数 `z = f(x, y)` 定义的曲面之上的区域，其体积可以通过二重积分计算：

V = ∬[f(x, y)] dA

其中，`dA` 表示区域的面积元素。

**示例：**

计算由函数 `z = x^2 + y^2` 定义的曲面在区域 `R = {(x, y) | x^2 + y^2 ≤ 1}` 上方的体积。

% 定义函数
f = @(x, y) x.^2 + y.^2;

% 定义积分区域
R = @(x, y) x.^2 + y.^2 <= 1;

% 计算体积
V = integral2(f, -1, 1, -1, 1, 'RelTol', 1e-6);
disp(['体积：', num2str(V)]);

**表面积计算**

对于一个由函数 `z = f(x, y)` 定义的曲面，其表面积可以通过二重积分计算：

S = ∬[√(1 + (∂z/∂x)^2 + (∂z/∂y)^2)] dA

其中，`∂z/∂x` 和 `∂z/∂y` 分别表示曲面在 `x` 和 `y` 方向的偏导数。

**示例：**

计算由函数 `z = x^2 + y^2` 定义的曲面在区域 `R = {(x, y) | x^2 + y^2 ≤ 1}` 上的表面积。

% 定义函数
f = @(x, y) x.^2 + y.^2;

% 定义积分区域
R = @(x, y) x.^2 + y.^2 <= 1;

% 计算表面积
S = integral2(@(x, y) sqrt(1 + (2*x)^2 + (2*y)^2), -1, 1, -1, 1, 'RelTol', 1e-6);
disp(['表面积：', num2str(S)]);

# 4. MATLAB二重积分的进阶应用

### 4.1 不规则区域的积分

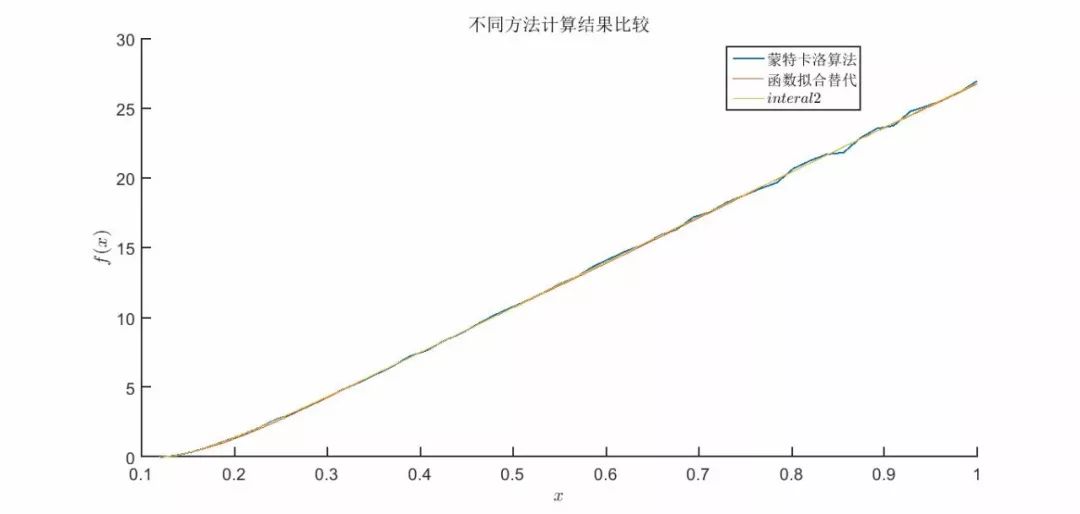
对于具有不规则形状的区域，传统的二重积分方法可能无法直接应用。MATLAB提供了两种强大的技术来处理此类问题：蒙特卡罗方法和网格自适应方法。

#### 4.1.1 使用蒙特卡罗方法

蒙特卡罗方法是一种随机采样技术，通过生成大量随机点来近似积分。对于不规则区域，蒙特卡罗方法可以有效地估计积分值，因为随机点可以覆盖整个区域。

% 定义积分函数
f = @(x, y) exp(-(x^2 + y^2));

% 定义积分区域
xmin = -2;
xmax = 2;
ymin = -2;
ymax = 2;

% 生成随机点
N = 10000;  % 随机点数量
x = xmin + (xmax - xmin) * rand(N, 1);
y = ymin + (ymax - ymin) * rand(N, 1);

% 计算积分值
integral = (xmax - xmin) * (ymax - ymin) * mean(f(x, y));

disp(['蒙特卡罗方法估计的积分值为：' num2str(integral)]);

#### 4.1.2 使用网格自适应方法

网格自适应方法是一种迭代算法，它通过细分网格来提高积分精度。在每个迭代中，算法会识别网格中积分误差最大的区域，并细分该区域以提高精度。

% 定义积分函数
f = @(x, y) exp(-(x^2 + y^2));

% 定义积分区域
xmin = -2;
xmax = 2;
ymin = -2;
ymax = 2;

% 设置网格自适应参数
max_level = 5;  % 最大网格细分级别
tolerance = 1e-6;  % 误差容忍度

% 调用网格自适应积分函数
integral = integral2(@(x, y) f(x, y), xmin, xmax, ymin, ymax, 'RelTol', tolerance, 'MaxLevel', max_level);

disp(['网格自适应方法估计的积分值为：' num2str(integral)]);

### 4.2 奇异积分的处理

奇异积分是指积分区域内存在奇点或不连续点的积分。对于此类积分，传统的积分方法可能会失效。MATLAB提供了两种技术来处理奇异积分：正则化技术和积分变换。

#### 4.2.1 使用正则化技术

正则化技术通过修改积分函数或积分区域来消除奇点或不连续点。例如，对于具有奇点的积分，可以使用正则化参数来平滑奇点附近的函数。

% 定义积分函数
f = @(x) 1 ./ (x - 0.5);

% 定义积分区域
a = 0;
b = 1;

% 设置正则化参数
epsilon = 1e-6;

% 调用正则化积分函数
integral = integral(@(x) f(x + epsilon), a, b);

disp(['正则化方法估计的积分值为：' num2str(integral)]);

#### 4.2.2 使用积分变换

积分变换是一种将奇异积分转换为非奇异积分的技术。例如，对于具有跳跃不连续点的积分，可以使用傅里叶变换将积分转换为频域，然后在频域中计算积分。

% 定义积分函数
f = @(x) heaviside(x - 0.5) - heaviside(x - 1);

% 定义积分区域
a = 0;
b = 1;

% 调用傅里叶变换
F = fft(f(linspace(a, b, 1000)));

% 计算积分值
integral = (b - a) * sum(real(F)) / length(F);

disp(['傅里叶变换方法估计的积分值为：' num2str(integral)]);

# 5. MATLAB二重积分的调试和优化

### 5.1 常见错误和解决方法

在使用MATLAB进行二重积分时，可能会遇到以下常见错误：

- **函数未收敛：**确保积分函数在积分区域内连续且有界。
- **结果不准确：**增加积分点数或使用更精确的积分方法。
- **语法错误：**仔细检查代码是否存在语法错误，例如括号不匹配或函数名称拼写错误。
- **内存不足：**对于大规模积分，确保有足够的内存。
- **数值不稳定：**使用稳定性更高的积分方法，例如高斯-勒让德求积法。

### 5.2 性能优化策略

为了提高MATLAB二重积分的性能，可以采用以下优化策略：

#### 5.2.1 向量化代码

使用向量化操作可以显著提高代码效率。例如，使用矩阵乘法代替嵌套循环来计算积分和。

% 嵌套循环
for i = 1:n
    for j = 1:m
        F(i, j) = f(x(i), y(j));
    end
end

% 向量化操作
F = f(x, y);

#### 5.2.2 并行计算

对于大规模积分，可以使用并行计算来加速计算。MATLAB提供了并行计算工具箱，允许在多核处理器或集群上并行执行代码。

% 并行计算
parfor i = 1:n
    for j = 1:m
        F(i, j) = f(x(i), y(j));
    end
end