Logisim数据表示：位运算的奥秘与应用


参考资源链接：[Logisim实验教程：海明编码与解码技术解析](https://wenku.csdn.net/doc/58sgw98wd0?spm=1055.2635.3001.10343)
# 1. Logisim与数据表示的基本概念

## 数据表示基础

在计算机科学中，数据表示是理解和操作信息的核心。使用Logisim工具，我们可以直观地探索数据的二进制表示。Logisim是一个用于设计和模拟数字逻辑电路的教育性工具，它允许用户构建各种数字逻辑电路，包括基本的逻辑门、算术运算单元，甚至是CPU的简化模型。

### Logisim界面介绍

打开Logisim后，我们可以看到几个主要的界面元素：

- **工具箱**：包含了各种逻辑门和辅助工具。
- **侧边栏**：显示了当前项目中使用的组件，如逻辑门、输入输出端口等。
- **画布**：是设计电路的主要区域。

### 数据的基本表示

数据在计算机中是以二进制形式表示的，每个二进制位称为一个比特（bit），它是信息的最小单位。通过二进制数，我们能够构建更复杂的表示，如字节（byte），这是8个比特的组合，能够表示256种不同的值。

二进制的运算和表示为位运算打下了基础。通过位运算，我们可以在不转换为十进制或其他进制数的情况下直接在二进制数上执行数学运算。这在硬件层面尤其重要，因为它提高了处理速度并简化了逻辑设计。

### 二进制与十进制的转换

理解二进制与十进制的转换对于掌握数据表示至关重要。在Logisim中，我们可以直接查看一个数字的二进制形式和它的十进制等价物，这有助于加深对数据表示转换过程的理解。在实践中，进行这类转换通常涉及使用二进制的位权重（即2的幂次方），这可以帮助我们快速从十进制转换到二进制，反之亦然。

通过本章，我们将为后续章节中位运算的深入分析和应用打下坚实的基础。无论是对于新手还是经验丰富的IT从业者，理解和操作这些基本概念都是提升数字逻辑设计能力的关键步骤。

# 2. 位运算的理论基础

## 2.1 位运算的基本原理

### 2.1.1 位运算的定义和类型

位运算是对二进制位直接进行的运算，包括AND、OR、XOR、NOT、移位等操作。这些操作是计算机中最基本的操作之一，对于系统软件开发以及硬件设计都至关重要。

#### AND运算

在AND运算中，只有两个对应位都为1时，结果位才为1，否则为0。例如：

  1 AND 1 = 1
  1 AND 0 = 0
  0 AND 1 = 0
  0 AND 0 = 0

#### OR运算

在OR运算中，只要两个对应位中有1个或2个为1，结果位就为1。例如：

  1 OR 1 = 1
  1 OR 0 = 1
  0 OR 1 = 1
  0 OR 0 = 0

#### XOR运算

XOR运算，即“异或”运算，当两个对应位不相同时结果位为1，相同时为0。例如：

  1 XOR 1 = 0
  1 XOR 0 = 1
  0 XOR 1 = 1
  0 XOR 0 = 0

#### NOT运算

NOT运算通常表示为一个一元运算符，对一个二进制位进行取反操作，即将1变为0，将0变为1。

#### 移位运算

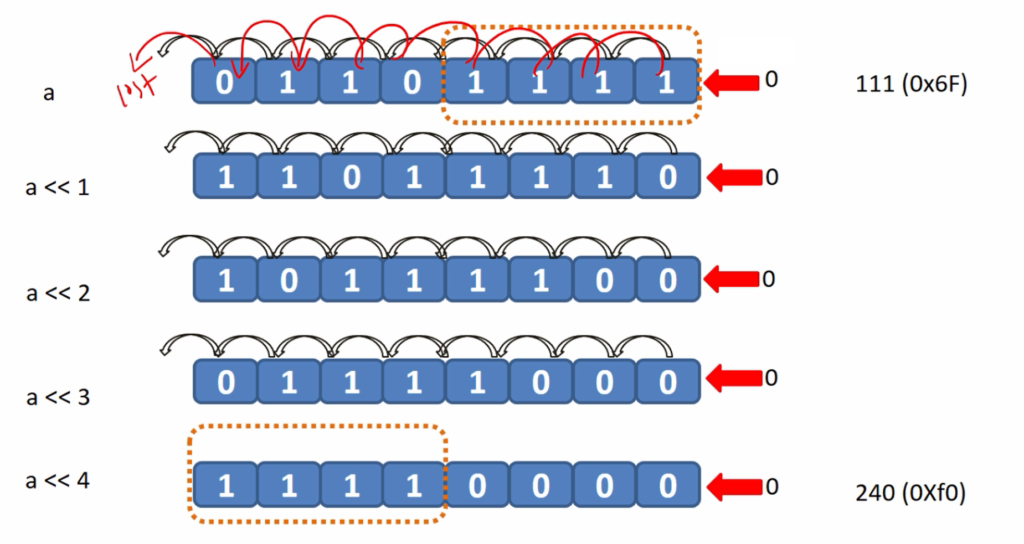
移位运算包括左移（<<）和右移（>>）。左移一位相当于乘以2，右移一位相当于除以2。在右移时，根据语言的不同，可以是逻辑右移（填充0）或者算术右移（符号位不变）。

### 2.1.2 位运算的数学原理

位运算遵循布尔代数中的逻辑运算规则，它是一种数学逻辑，用来处理二进制数的运算。布尔代数中最基本的操作是AND、OR和NOT，这些操作可以组合起来表达更复杂的逻辑函数。

逻辑运算在数学上可以通过真值表来表示，真值表列出了所有可能输入值的组合以及对应的输出值。例如，AND运算的真值表如下：

| A | B | A AND B |
|---|---|---------|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |

位运算不仅是数字逻辑电路的基础，它也用于优化数据处理速度和降低资源消耗，在软件开发和硬件设计中发挥着巨大作用。

## 2.2 位运算的逻辑与应用

### 2.2.1 逻辑运算的应用场景

逻辑运算在计算机科学中有广泛的应用，它们在布尔逻辑、计算机体系结构、数字逻辑设计、以及算法优化等方面都扮演着关键角色。

- **布尔逻辑**：逻辑运算符是构成布尔表达式的基础，用于编程中的条件判断和决策。
- **计算机体系结构**：逻辑运算用于处理器的控制单元和数据路径中，实现指令的解码和执行。
- **数字逻辑设计**：在设计逻辑电路时，逻辑运算是设计简化和实现复杂功能的基础。
- **算法优化**：一些算法中利用位运算可以避免复杂的数学计算，提升效率。

### 2.2.2 逻辑运算在计算机中的表示

在计算机系统中，逻辑运算符通常被内嵌于硬件和软件层面，直接体现在编程语言中。例如：

// C语言中的逻辑运算示例
int a = 5; // 二进制表示为 101
int b = 3; // 二进制表示为 011

int and_result = a & b; // AND运算结果
int or_result = a | b;  // OR运算结果
int xor_result = a ^ b; // XOR运算结果

在上述代码中，`&`代表AND运算，`|`代表OR运算，而`^`代表XOR运算。这样的运算直接在底层硬件层面执行，效率极高。

## 2.3 二进制数与十进制数的转换

### 2.3.1 二进制与十进制转换方法

二进制与十进制之间的转换是数据表示的基础。以下是一些基础的转换方法：

**二进制转十进制：**

要将一个二进制数转换为十进制数，需要将每个二进制位乘以2的幂次方，然后将结果相加。例如，二进制数`1011`转换为十进制数是：

1*2^3 + 0*2^2 + 1*2^1 + 1*2^0 = 8 + 0 + 2 + 1 = 11

**十进制转二进制：**

十进制转二进制的方法是不断地将十进制数除以2，记录下每次的余数，然后将余数反向排列。例如，十进制数`11`转换为二进制数是：

11 / 2 = 5 ... 1
5 / 2 = 2 ... 1
2 / 2 = 1 ... 0
1 / 2 = 0 ... 1

将余数反向排列得到`1011`。

### 2.3.2 转换技巧与实践案例

掌握转换技巧能够帮助我们快速准确地进行转换。例如，在二进制转换为十进制时，可以使用幂的技巧，而在十进制转换为二进制时，则可以利用位运算的快速幂运算。

#### 实践案例

假设我们需要将十进制数`25`转换为二进制数。使用快速幂运算的技巧：

def dec_to_bin(n):
    binary = ''
    while n > 0:
        binary = str(n % 2) + binary
        n = n // 2
    return binary

# 将十进制数转换为二进制数
dec_number = 25
bin_number = dec_to_bin(dec_number)
print(f"十进制数 {dec_number} 对应的二进制数为: {bin_number}")

输出结果为：`十进制数 25 对应的二进制数为: 11001`

在本章节中，我们详细讨论了位运算的理论基础，包括位运算的定义、类型、逻辑运算的应用场景以及二进制数与十进制数之间的转换方法和技巧。这些知识对于理解和运用位运算至关重要，并将在后续章节中继续探讨其在实践和进阶位运算技巧中的应用。

# 3. 位运算的实践技巧

位运算在计算机科学领域扮演着至关重要的角色，它的应用覆盖了从底层硬件操作到高级算法优化的各个层面。在这一章中，我们将深入探讨位运算的实践技巧，包括位运算操作的实现、在Logisim中的操作以及算法优化策略。

## 3.1 常用位运算操作的实现

位运算操作通常包括AND、OR、XOR和NOT等基本运算，以及左移、右移等移位操作。这些操作是构建更复杂数据结构和算法的基础。

### 3.1.1 AND, OR, XOR, NOT操作详解

在逻辑运算中，AND、OR、XOR和NOT是四种基本的位运算操作。理解这些操作有助于我们掌握更高级的位运算技巧。

#### AND操作
AND操作用于检查两个位是否都是1。只有当两个操作数的对应位都是1时，结果位才是1，否则为0。AND操作的逻辑可以用来清除位中的某些位，即保留某些位为1而将其他位置为0。

**代码示例:**

unsigned char a = 0b11001100; // 12位和13位为1，其他位为0
unsigned char b = 0b11110000; // 8位到11位为1，其他位为0
unsigned char result = a & b; // 应用AND操作
// 结果为0b11000000，即只保留了a和b共有的高位1

在上述代码中，变量`a`和`b`进行AND操作，只有当两个操作数的位都为1时，结果的对应位才为1。

#### OR操作
OR操作检查两个位，如果其中一个或两个都是1，则结果位为1；只有当两个位都是0时，结果位才是0。OR操作常用于设置位中的某些位为1，而不影响其他位。

**代码示例:**

unsigned char a = 0b11001100; // 12位和13位为1，其他位为0
unsigned char b = 0b00001111; // 1位到4位为1，其他位为0
unsigned char result = a | b; // 应用OR操作
// 结果为0b11001111，即在a的基础上将低四位设置为1

在上述代码中，`a`和`b`进行OR操作后，`b`中的低四位都被设置为1。

#### XOR操作
XOR（异或）操作比较两个位，当两个位不相同时结果位为1，相同时为0。XOR操作的特性使其在翻转位时非常有用。

**代码示例:**

unsigned char a = 0b11001100; // 12位和13位为1，其他位为0
unsigned char b = 0b10101010; // 奇数位为1，偶数位为0
unsigned char result = a ^ b; // 应用XOR操作
// 结果为0b01100110，即翻转了a中偶数位上的0和奇数位上的1

在上述代码中，`a`和`b`进行XOR操作后，`a`中的偶数位上的0变成了1，奇数位上的1变成了0。

#### NOT操作
NOT操作（按位取反）是一个单目运算符，它将操作数的所有位取反，即将1变为0，将0变为1。NOT操作常用于清除位中的某些位，或者用于掩码的生成。

**代码示例:**

unsigned char a = 0b11001100; // 12位和13位为1，其他位为0
unsigned char result = ~a;    // 应用NOT操作
// 结果为0b00110011，即a中所有位都被取反

在上述代码中，`a`进行N