Matlab数据平滑技巧大公开：提升数据质量的关键步骤


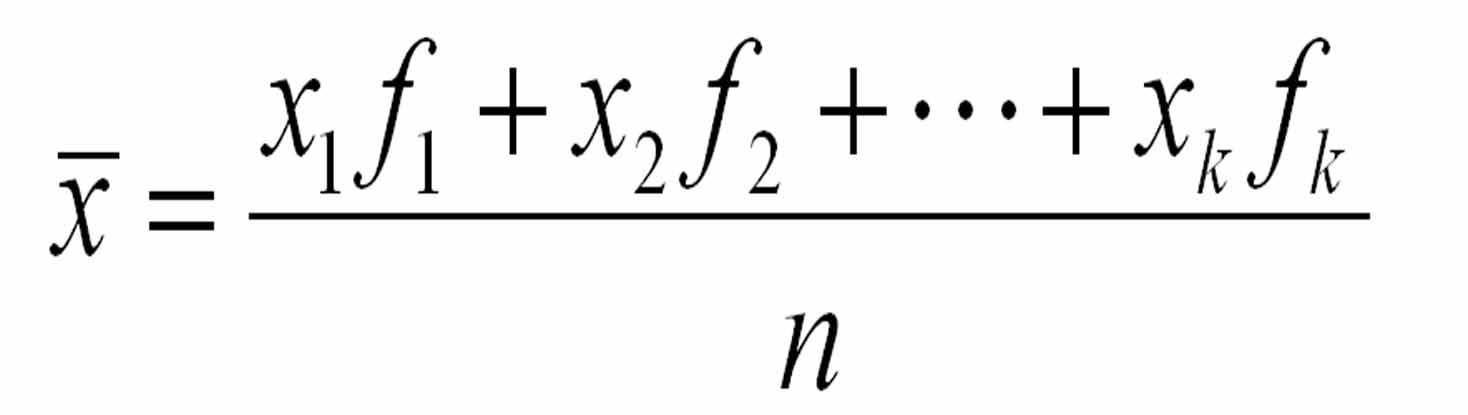
# 摘要
本文综述了Matlab中数据平滑的各种技术，从基础到高级方法，以及它们的应用和挑战。首先介绍了数据平滑的目的和意义，以及不同平滑技术的分类和应用场景。接着，详细探讨了简单移动平均法、加权移动平均法、指数平滑法、季节性指数平滑法和局部加权回归平滑法的原理及其在Matlab中的实现。进一步，本文分析了多项式平滑、小波变换平滑和交互式数据平滑工具的高级应用，以及它们在处理科学数据和经济数据时的案例分析。最后，讨论了在大数据环境下数据平滑面临的挑战和未来发展趋势，指出当前技术的局限性并预测未来方向。

# 关键字
数据平滑；Matlab；移动平均法；指数平滑；小波变换；大数据环境

参考资源链接：[Matlab数据预处理：异常值剔除与平滑处理详解](https://wenku.csdn.net/doc/7qy2ufgtpp?spm=1055.2635.3001.10343)
# 1. Matlab数据平滑概述

在数据分析和处理的领域中，数据平滑是一项核心技术，旨在减少数据中的随机波动，使数据的趋势更加清晰。它在信号处理、经济学、生物学和其它科学领域都有广泛的应用。通过平滑技术，可以使得数据更加稳定，从而让数据的趋势和模式更容易被识别和分析。Matlab作为一种强大的数学计算与可视化工具，提供了丰富的函数和工具箱，支持各种数据平滑方法，是数据科学家和工程师处理时间序列和信号分析的首选平台。在本文中，我们将深入探讨Matlab中实现数据平滑的各种方法，从基础到高级，包括移动平均法、指数平滑法、局部加权回归等。同时，我们还将分析这些方法在不同领域的应用案例，并探讨数据平滑在大数据背景下的挑战与未来发展趋势。通过本章概述，读者将对数据平滑有一个全面的认识，为后续章节的深入学习打下基础。

# 2. 基础数据平滑技术

## 2.1 数据平滑理论基础

### 2.1.1 数据平滑的目的和意义
数据平滑的目的是从含有噪声的数据中提取有用信息，减少数据中的随机波动，从而使潜在的趋势变得更加清晰。这项技术在时间序列分析、信号处理和图像处理等领域中尤为重要。数据平滑的意义在于它能够提供数据的简化的、更加容易理解的表示，帮助分析师在复杂数据集中识别模式和趋势。

### 2.1.2 平滑技术的分类和应用场景
数据平滑技术大致可以分为两类：局部平滑和全局平滑。局部平滑方法（如移动平均法）通过考虑数据点附近的一小部分数据来进行平滑处理，而全局平滑方法（如多项式平滑）则考虑整个数据集以拟合一个平滑曲线。局部方法适合在趋势不明显或者局部特征需要强调时使用，全局方法则更适用于整体趋势需要描绘时。在实际应用中，选择何种方法取决于数据的特性和分析的需求。

## 2.2 简单移动平均法

### 2.2.1 移动平均法的原理
简单移动平均法是一种基础的数据平滑技术，它通过计算数据序列中连续时间段内数值的平均值来进行平滑。这种方法的有效性基于一个假设：短期内的随机波动或噪声，随着时间段的增加，其对整体平均值的影响会逐渐减小。因此，通过移动平均法得到的平均值序列能够更好地反映出数据的总体趋势。

### 2.2.2 实际应用：时间序列数据平滑实例
在Matlab中，可以使用`movmean`函数实现简单移动平均法。下面给出一个时间序列数据平滑的实例代码：

% 假设x为需要平滑的时间序列数据，n为窗口大小
x = [1, 2, 4, 7, 11, 16, 22, 29, 37, 46, 56]; % 示例时间序列数据
n = 3; % 移动平均的窗口大小
smoothed_x = movmean(x, n); % 计算移动平均值

% 绘制原始数据和移动平均后的数据对比图
figure;
plot(x, 'o-', 'DisplayName', 'Original Data');
hold on;
plot(smoothed_x, 'x-', 'DisplayName', 'Smoothed Data');
legend;
xlabel('Time');
ylabel('Value');
title('Simple Moving Average Example');

执行上述代码后，会得到一个包含原始数据和移动平均值的图表，从而清晰地展示出移动平均法对时间序列数据的平滑效果。

## 2.3 加权移动平均法

### 2.3.1 权重的选取及其影响
加权移动平均法通过为数据点分配不同的权重，从而控制其在计算平均值时的影响程度。权重的选取通常依赖于数据点的位置和重要性，距离当前点越近的数据点可以赋予更大的权重。这种权重的分配方式使得加权移动平均法能够更好地反映数据的最新趋势和变化，同时还能降低旧数据对当前趋势的影响。

### 2.3.2 加权移动平均法在Matlab中的实现
Matlab提供了`filter`函数，允许用户自定义一个权重数组来实现加权移动平均。下面展示了一个简单的加权移动平均实现代码段：

% 假设x为需要平滑的数据，weights为自定义的权重数组
x = [1, 2, 4, 7, 11, 16, 22, 29, 37, 46, 56]; % 示例数据
weights = [0.1, 0.2, 0.4, 0.2, 0.1]; % 自定义权重
smoothed_x = filter(weights, 1, x); % 应用加权移动平均

% 绘制原始数据和加权移动平均后的数据对比图
figure;
stem(x, 'o-', 'DisplayName', 'Original Data');
hold on;
stem(smoothed_x, 'x-', 'DisplayName', 'Weighted Smoothed Data');
legend;
xlabel('Index');
ylabel('Value');
title('Weighted Moving Average Example');

在上述代码中，`filter`函数的第一个参数是权重数组，第二个参数为1表示权重数组和输入数组长度相同，第三个参数为需要平滑的数据序列。运行后，通过图形化界面展示出原始数据与经过加权移动平均后的数据，突出展示了数据平滑的效果。

以上是第二章：基础数据平滑技术的详细章节内容。接下来，我们将在第三章中深入探讨高级数据平滑方法。

# 3. 高级数据平滑方法

## 3.1 指数平滑法

### 3.1.1 指数平滑法的基本原理

指数平滑法是一种非常有效的预测技术，尤其适用于处理具有趋势或季节性特点的时间序列数据。其核心思想是给予更近期的观测值更高的权重，而较远期的观测值则赋予较低的权重。这样做的目的是让模型对最近的变化趋势更为敏感，同时淡化早期数据的影响，从而提高预测的准确性。

指数平滑方法通过一个称为平滑系数（或称指数平滑参数）的α值来控制权重的分配，α的取值范围在0到1之间。当α值接近1时，模型将赋予最近的观测值更大的权重；反之，当α值接近0时，模型对观测值的反应将更为迟钝，波动较小。

### 3.1.2 不同α值对平滑效果的影响

不同的α值对于平滑效果的影响是显著的。选择合适的α值是指数平滑法应用中的一个关键步骤。一般情况下，α值的选择需要根据实际数据的特点和预测需求来进行。如果数据变化剧烈，或者需要快速响应最近的数据变化，通常会选择较大的α值。而如果数据相对平稳，或者对短期波动不敏感，可能会选择较小的α值。

在Matlab中实现指数平滑时，可以通过优化算法来自动选择最佳的α值，或者根据经验或专业知识来手动设定α值。下面展示了一个简单的指数平滑法在Matlab中的实现示例：

% 假设y为需要平滑的时间序列数据
y = [12, 15, 17, 18, 19, 20, 21, 21, 22, 22, 23, 24, 25, 26, 27, 28];
alpha = 0.5;  % 设置平滑系数

% 初始化平滑后的序列
smoothed = zeros(size(y));

% 执行指数平滑
for i = 2:length(y)
    smoothed(i) = alpha * y(i) + (1 - alpha) * smoothed(i-1);
end