MATLAB控制系统稳定性分析：深入工具箱内部，掌握稳定性工具

# 1. MATLAB控制系统稳定性分析基础

MATLAB（Matrix Laboratory）是一个功能强大的数学计算和可视化软件包，广泛应用于工程和科学研究。在控制系统领域，MATLAB提供了一个名为Control System Toolbox（控制工具箱）的附加产品，它为控制系统的设计、分析和仿真提供了丰富的工具和函数。

## 1.1 控制系统稳定性的定义

稳定性是控制系统分析中的核心概念。一个系统被认为是稳定的，如果在受到有界输入的情况下，系统的输出也能保持有界的。对于线性时不变（LTI）系统，稳定性可以通过其传递函数或状态空间表示来分析。

## 1.2 控制系统稳定性的分析方法

在MATLAB中，我们可以使用多种方法来分析控制系统稳定性。例如，通过分析系统的极点位置，我们可以判断一个线性系统的稳定性。一个系统稳定当且仅当其所有的极点都具有负实部。

此外，MATLAB中的`pole`函数可以直接用来计算传递函数的极点，从而快速判断系统的稳定性状态。

% 示例代码计算传递函数极点
num = [1]; % 分子多项式系数
den = [1, 3, 2]; % 分母多项式系数
sys = tf(num, den); % 创建传递函数模型
poles = pole(sys); % 计算极点
disp(poles); % 显示极点

执行上述代码后，我们可以通过极点的位置来判断系统是否稳定。如果所有极点的实部都为负，则系统稳定；如果存在实部为正的极点，则系统不稳定。此外，MATLAB还提供了多种函数和工具用于绘制根轨迹图（`rlocus`）、奈奎斯特图（`nyquist`）和波德图（`bode`），这些图形化工具同样可以用于稳定性的直观分析。

通过本章的学习，你将掌握MATLAB进行控制系统稳定性分析的基础知识，为后续更深入的学习打下坚实基础。

# 2. MATLAB控制工具箱的理论基础

### 2.1 系统稳定性的数学概念

#### 2.1.1 稳定性定义和分类

系统稳定性在数学和工程领域是一个核心概念，它描述了一个系统在受到外部扰动或初始状态偏差时，是否能保持或者恢复其特定的行为或平衡状态。稳定性可以被分为几种类型，其中最重要的是内部稳定性和外部稳定性。

内部稳定性关注系统本身，指的是系统对所有初始状态的响应是否随时间趋于零。而外部稳定性则关注系统的输出，即系统是否能在有界输入的情况下产生有界输出（BIBO稳定性）。

在控制系统分析中，一个系统被分类为稳定，意味着它能抵抗外部的扰动，并且随着时间的推移，如果初始扰动被移除，系统将恢复到其原始状态或者达到一个新的稳定状态。这种稳定性分析对于设计安全和可靠的控制系统至关重要。

#### 2.1.2 稳定性的数学模型

数学上，系统稳定性的分析通常涉及到差分方程或者微分方程。一个线性时不变系统（LTI）可以用以下常微分方程表示：

a_n \frac{d^n y(t)}{dt^n} + a_{n-1} \frac{d^{n-1} y(t)}{dt^{n-1}} + ... + a_0 y(t) = b_m \frac{d^m x(t)}{dt^m} + b_{m-1} \frac{d^{m-1} x(t)}{dt^{m-1}} + ... + b_0 x(t)

其中，`y(t)` 是系统的输出，`x(t)` 是输入，`a_i` 和 `b_j` 是系统参数。对于稳定性分析，我们需要考虑系统的特征方程，这是由系统方程的系数得到的一个多项式方程。根据劳斯-赫尔维茨稳定性判据，如果所有特征值的实部均为负，则系统是稳定的。

### 2.2 控制系统的基本理论

#### 2.2.1 开环和闭环系统

在控制系统中，开环系统是输出不反馈到输入端的系统，它不依赖于之前的输出来调整其当前或未来的输出。相比之下，闭环系统（或者反馈系统）会将系统的输出部分地反馈到输入端，形成一个闭环路径。

闭环系统设计的核心在于反馈，它能够对系统的行为进行调整以达到期望的性能，如改善稳定性、减少误差和增加系统鲁棒性。MATLAB提供了丰富的工具箱来模拟和分析这两种类型的系统。

#### 2.2.2 线性时不变系统(LTI)

LTI系统是控制理论中的一个基本概念，描述了系统输入与输出之间的线性关系，并且系统的参数不随时间变化。这种系统在数学上易于分析，许多系统的稳定性质可以通过其传递函数来研究。

在MATLAB中，使用控制工具箱可以方便地处理LTI系统。传递函数是LTI系统的一种数学表示方法，通常表示为两个多项式之比，分别对应于输出和输入。

num = [2 5 1]; % 分子多项式系数
den = [1 3 2]; % 分母多项式系数
sys = tf(num, den); % 创建传递函数模型

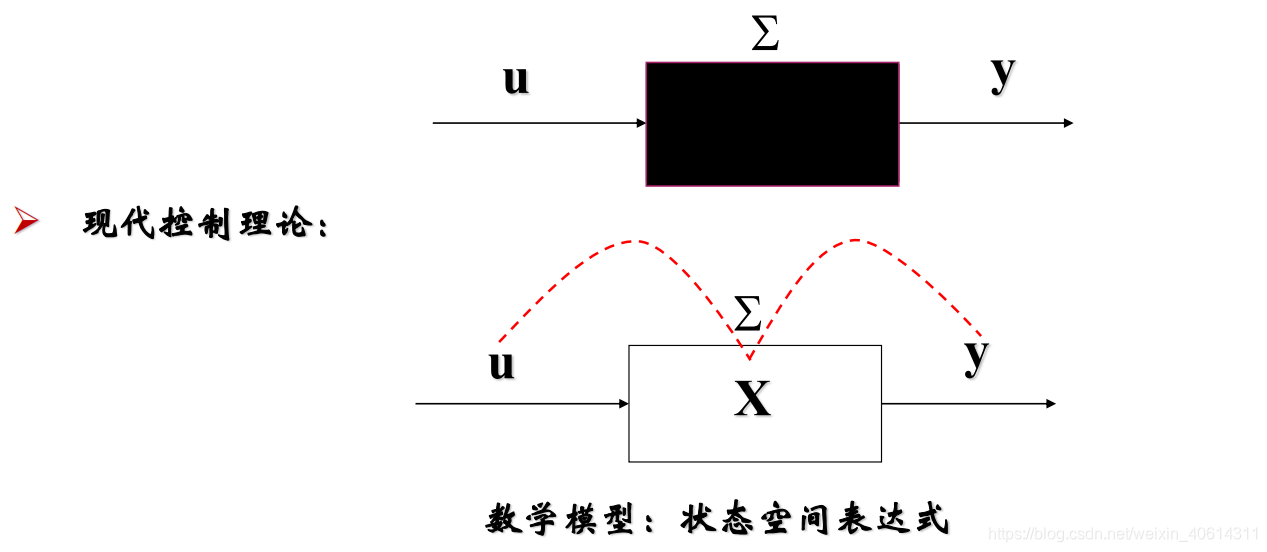
#### 2.2.3 系统的传递函数和状态空间表示

传递函数是LTI系统分析中非常重要的工具，它简化了系统的分析和设计过程。然而，对于复杂的多变量系统，状态空间表示是一种更为强大的数学模型。它描述了系统内部状态随时间的变化，以及如何从输入到输出。

状态空间模型由状态方程和输出方程组成：

% 状态方程
dx/dt = A*x + B*u
% 输出方程
y = C*x + D*u

A = [0 1; -a -b]; % 状态矩阵
B = [0; 1];        % 输入矩阵
C = [1 0];         % 输出矩阵
D = 0;             % 直接传输矩阵

使用MATLAB的`ss`函数，我们可以很容易地创建状态空间模型并进行分析。

### 2.3 控制工具箱中的稳定性判据

#### 2.3.1 Routh-Hurwitz判据

Routh-Hurwitz判据是一种用于判断线性时不变系统稳定性的数学工具。这个方法基于系统的特征方程，不需计算方程的根，而是通过构造一个特殊的Routh表来进行判断。

在MATLAB中，我们可以使用`rlocus`函数来得到系统的根轨迹图，从图中可以直观地判断系统稳定性的边界。

num = [2 5 1]; % 分子多项式系数
den = [1 3 2]; % 分母多项式系数
sys = tf(num, den);
rlocus(sys);

#### 2.3.2 Nyquist判据

Nyquist稳定性判据也是分析系统稳定性的一个重要工具，它是通过绘制系统的开环频率响应来判断闭环系统的稳定性。

在MATLAB中，`nyquist`函数可以用来绘制Nyquist图。从这个图中，我们可以确定系统稳定性的充分必要条件，即开环系统增益交叉频率和相位交叉频率的数量关系。

nyquist(sys);
title('Nyquist Plot');
grid on;

#### 2.3.3 Bode图与系统稳定性

Bode图是系统频率响应的另一种图形表示，它包括幅度图和相位图。通过观察Bode图，我们可以直观地判断系统是否稳定，也可以对系统进行初步的性能评估。

使用MATLAB的`bode`函数，我们可以获得系统的Bode图，并进一步分析系统的频率特性。

bode(sys);
title('Bode Plot');
grid on;

通过上述各种判据和分析方法，MATLAB为控制系统工程师提供了一套完善的理论基础工具，帮助他们深入理解系统的稳定性，并对控制系统的性能进行优化。

# 3. MATLAB控制工具箱的实践应用

在控制系统设计和分析的领域，MATLAB提供了一个强大的控制工具箱，使得工程师和研究人员可以更高效地构建、分析和调整控制系统的性能。控制工具箱不仅包含了系统建模、分析和设计的基本功能，还提供了丰富的算法和工具以应对各种复杂的问题。本章节将深入探讨如何在MATLAB控制工具箱中实现系统的建模、分析和校正。

## 3.1 系统建模与分析工具

### 3.1.1 使用tf和ss创建系统模型

MATLAB中的`tf`函数用于创建传递函数模型，而`ss`函数则用于创建状态空间表示的模型。这两种模型是控制系统分析中最常用的数学表示形式。传递函数模型适合描述线性时不变系统(LTI)的输入-输出关系，而状态空间模型则适合分析系统内部状态的动态特性。

% 创建一个传递函数模型
num = [1]; % 分子多项式系数
den = [1, 3, 2]; % 分母多项式系数
sys_tf = tf(num, den); % 创建传递函数模型

% 创建一个状态空间模型
A = [-1, -2; 1, 0]; % 状态矩阵
B =