STM32单片机复位电路时序优化：实战案例

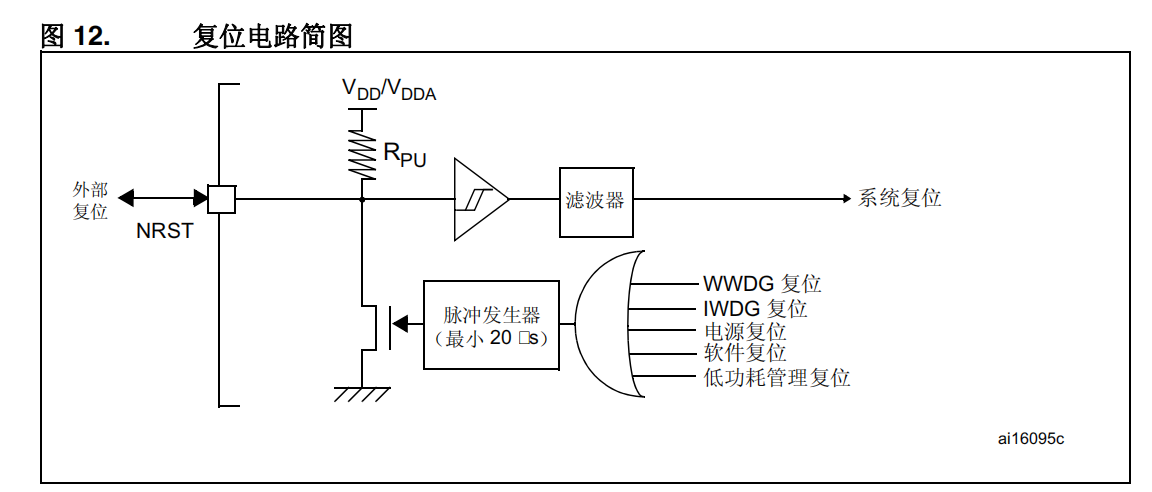
# 1. STM32单片机复位电路概述**

复位电路是STM32单片机中不可或缺的一部分，它负责在单片机上电或复位时将所有寄存器和存储器重置为初始状态。复位电路的时序对于单片机正常工作至关重要，如果时序不正确，可能会导致单片机无法正常启动或运行不稳定。

本章将对STM32单片机的复位电路进行概述，包括复位电路的组成、工作原理以及时序要求。

# 2. 复位电路时序优化理论

### 2.1 复位电路的时序要求

复位电路的时序要求主要包括以下几个方面：

- **复位脉冲宽度：**复位脉冲的宽度必须满足单片机的最小复位时间要求。对于STM32单片机，最小复位时间通常为20ms。
- **复位脉冲上升沿时间：**复位脉冲的上升沿时间必须满足单片机的最小上升沿时间要求。对于STM32单片机，最小上升沿时间通常为10ns。
- **复位脉冲下降沿时间：**复位脉冲的下降沿时间必须满足单片机的最小下降沿时间要求。对于STM32单片机，最小下降沿时间通常为10ns。
- **复位脉冲稳定时间：**复位脉冲在高电平或低电平上的稳定时间必须满足单片机的最小稳定时间要求。对于STM32单片机，最小稳定时间通常为100ns。

### 2.2 复位电路的优化原则

复位电路的优化原则主要包括以下几个方面：

- **最小化复位脉冲宽度：**复位脉冲宽度应尽可能接近单片机的最小复位时间要求，以减少复位过程中的延时。
- **缩短复位脉冲上升沿时间和下降沿时间：**复位脉冲的上升沿时间和下降沿时间应尽可能短，以减少复位过程中的毛刺和干扰。
- **延长复位脉冲稳定时间：**复位脉冲在高电平或低电平上的稳定时间应尽可能长，以确保单片机能够可靠地复位。
- **选择合适的复位电路：**复位电路的类型应根据单片机的具体要求和应用场景进行选择。常用的复位电路包括外部复位电路和内部复位电路。

# 3. 复位电路时序优化实践

### 3.1 外部复位电路的优化

#### 3.1.1 电容值的选择

外部复位电路中，电容值的选择至关重要。电容值过小会导致复位时间不足，而电容值过大则会延长复位时间，影响系统启动速度。

- **选择原则：**电容值应满足以下公式：

C ≥ (t_reset - t_debounce) / R

其中：

- `C`：电容值
- `t_reset`：复位时间
- `t_debounce`：去抖时间
- `R`：电阻值

- **推荐值：**一般情况下，电容值选择在 0.1μF 至 1μF 之间。

#### 3.1.2 电阻值的选择

电阻值的选择也影响复位电路的时序。电阻值过小会导致复位时间过短，而电阻值过大则会延长复位时间。

- **选择原则：**电阻值应满足以下公式：

R ≤ (Vcc - V_reset) / I_reset

其中：

- `R`：电阻值
- `Vcc`：电源电压
- `V_reset`：复位引脚电压
- `I_reset`：复位引脚电流

- **推荐值：**一般情况下，电阻值选择在 1kΩ 至 10kΩ 之间。

### 3.2 内部复位电路的优化

#### 3.2.1 看门狗复位的优化

看门狗复位是 STM32 单片机内部的一种复位机制。通过配置看门狗定时器，当系统长时间没有响应时，看门狗复位会自动触发。

- **优化原则：**
- 启用看门狗复位功能。
- 设置合适的看门狗定时器值。
- 定期刷新看门狗定时器。

- **代码示例：**

// 启用看门狗复位
RC