机器学习入门到实战：5大算法与案例应用剖析


参考资源链接：[研究生学术综合英语1-6课课文及翻译.pdf](https://wenku.csdn.net/doc/6460477e543f8444888da459?spm=1055.2635.3001.10343)
# 1. 机器学习基础与概念理解

在当今数字化世界中，机器学习已成为推动技术发展的重要力量。本章旨在为读者提供机器学习的基础知识和概念框架。

## 1.1 机器学习的定义
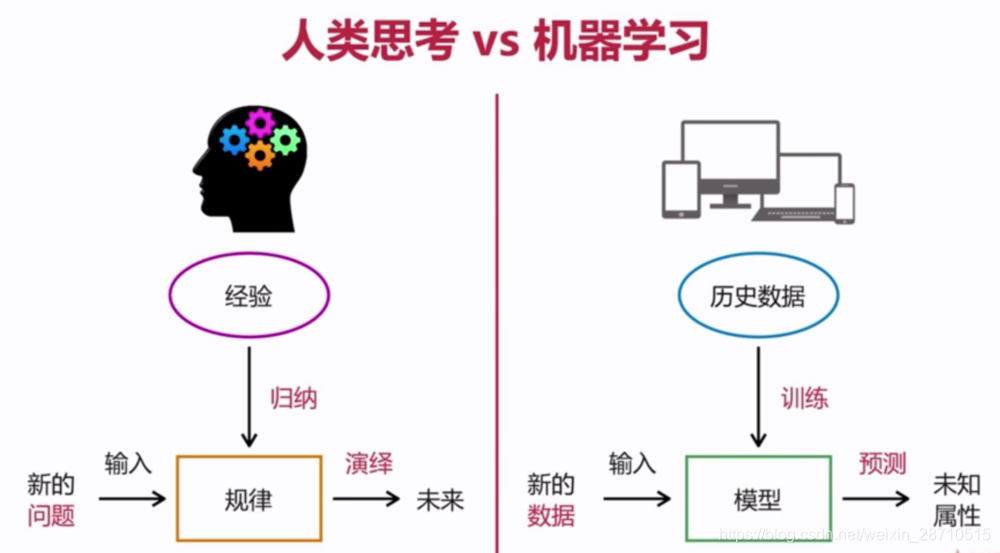
机器学习是一种通过算法使计算机系统能够从数据中学习并进行预测或决策的技术。它允许系统在没有明确编程的情况下，从经验中改进性能。

## 1.2 机器学习的主要类型
机器学习通常分为三大类：监督学习、无监督学习和强化学习。每种类型根据是否需要标签数据以及学习方式的不同而有所区别。

## 1.3 关键术语和概念
在深入学习算法之前，需要理解一些基本概念，如特征、标签、模型、训练集和测试集等。这些术语构成了机器学习工作的基础。

## 1.4 机器学习的发展历程与应用
从20世纪50年代的理论起源到如今在各种行业中的广泛应用，机器学习已经历了长足的发展。本章将简要概述这一发展历程，并探讨其应用案例。

机器学习的概念理解是建立专业知识体系的基石，下一章将深入探讨核心算法及其在Python中的实现。

# 2. 核心算法原理与实现

### 2.1 线性回归算法
#### 2.1.1 线性回归的数学基础

线性回归是统计学和机器学习中最基本的预测建模技术。在数学上，它尝试找到两个变量之间的关系，这种关系可以用一条直线来表示。线性回归的模型可以简单地表示为：

\[ y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_nx_n + \epsilon \]

其中，\( y \)是响应变量，\( x_1, x_2, \dots, x_n \)是预测变量，\( \beta_0, \beta_1, \dots, \beta_n \)是模型参数，而\( \epsilon \)是误差项，表示模型未能解释的随机变异。

在实际应用中，我们通过最小化误差的平方和（最小二乘法）来估计\( \beta \)参数，从而得到最优拟合线。

#### 2.1.2 线性回归在Python中的实现

利用Python进行线性回归分析，可以使用`scikit-learn`库中的`LinearRegression`类。下面是一个简单的线性回归实现的代码示例：

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import numpy as np
import pandas as pd

# 假设df是包含特征和目标变量的数据集
X = df.drop('target', axis=1)
y = df['target']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化线性回归模型
lr = LinearRegression()

# 训练模型
lr.fit(X_train, y_train)

# 预测测试集结果
y_pred = lr.predict(X_test)

# 计算模型的均方误差
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}')

通过这段代码，我们首先导入了必要的模块，然后划分数据集，并初始化了线性回归模型。之后，使用训练数据集来训练模型，并用测试数据集来评估模型的性能。最后，我们计算了模型预测的均方误差。

### 2.2 逻辑回归算法
#### 2.2.1 逻辑回归的理论基础

逻辑回归是分类问题中常用的算法，尽管名字中带有“回归”，但它实际上是一种分类方法。它的输出不是线性关系，而是介于0和1之间的概率，通常用来预测一个事件的发生概率。

逻辑回归模型可以表示为：

\[ P(Y=1) = \frac{1}{1 + e^{-(\beta_0 + \beta_1x_1 + \dots + \beta_nx_n)}} \]

其中\( P(Y=1) \)是给定特征\( x_1, x_2, \dots, x_n \)下，事件发生的概率。通过逻辑函数（Sigmoid函数），将线性回归的输出映射到(0,1)区间，以得到概率。

#### 2.2.2 逻辑回归在分类问题中的应用

逻辑回归在实际应用中，如信用评分、疾病诊断、邮件垃圾过滤等二分类问题中表现良好。下面是一个使用`scikit-learn`库的`LogisticRegression`类的实现示例：

from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split

# 假设df是包含特征和目标变量的数据集
X = df.drop('target', axis=1)
y = df['target']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化逻辑回归模型
lr = LogisticRegression()

# 训练模型
lr.fit(X_train, y_train)

# 预测测试集结果
y_pred = lr.predict(X_test)

# 计算模型的准确率
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy}')

在这段代码中，我们通过逻辑回归模型训练并预测了数据集的分类标签，并计算了模型的准确率，以评估模型性能。

### 2.3 决策树算法
#### 2.3.1 决策树的工作原理

决策树是一种类似于流程图的树结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，而每个叶节点代表一种分类结果。

在构建决策树时，算法会选择最佳特征进行分裂，以最大化子集的纯度。常用的决策树算法有ID3、C4.5和CART。不同的算法可能使用不同的标准来选择特征，比如信息增益、基尼不纯度或者均方误差。

#### 2.3.2 构建和优化决策树模型

构建决策树时需要考虑模型的复杂度和预测能力。一个树过于复杂可能会导致过拟合（即模型捕捉到了太多的训练数据的噪声），而一个树太简单则可能无法捕捉到数据的潜在结构，导致欠拟合。

from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
from sklearn.model_selection import GridSearchCV

# 假设df是包含特征和目标变量的数据集
X = df.drop('target', axis=1)
y = df['target']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化决策树模型
dt = DecisionTreeClassifier()

# 使用网格搜索优化超参数
parameters = {'max_depth': [2, 4, 6, 8, 10], 'min_samples_split': [2, 3, 4, 5]}
grid_search = GridSearchCV(dt, parameters, cv=5)
grid_search.fit(X_train, y_train)

# 输出最优参数和性能评估
best_dt = grid_search.best_estimator_
y_pred = best_dt.predict(X_test)
print(classification_report(y_test, y_pred))

在这个例子中，我们使用了`GridSearchCV`来进行超参数的优化，通过交叉验证来寻找最佳的树深度和分裂所需的最小样本数。之后，我们利用优化后的决策树模型来预测测试集，并输出分类报告来评估模型性能。

### 2.4 随机森林算法
#### 2.4.1 随机森林的构成原理

随机森林是一种集成学习方法，通过构建多个决策树并将它们的预测结果汇总起来以提高整体模型的准确性和泛化能力。每棵决策树都是在一个随机选取的训练子集上独立训练出来的，使用不同的特征子集，从而使得这些树之间彼此独立。

随机森林的最终预测结果是通过投票或者平均多个决策树的预测结果得出的。

#### 2.4.2 随机森林的实践与调优

随机森林算法的实现较为简单，但调优时需要注意的参数包括树的数量、树的深度、特征的数量以及最小样本分割数。调优的目标是找到最佳的参数组合来平衡模型的偏差和方差。

下面是一个使用`RandomForestClassifier`的随机森林模型实现和优化的例子：

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV

# 假设df是包含特征和目标变量的数据集
X = df.drop('target', axis=1)
y = df['target']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化随机森林模型
rf = RandomForestClassifier()

# 使用网格搜索优化超参数
parameters = {'n_estimators': [10, 50, 100], 'max_features': ['auto', 'sqrt', 'log2']}
grid_search = GridSearchCV(estimator=rf, param_grid=parameters, cv=5, n_jobs=-1)
grid_search.fit(X_train, y_train)

# 输出最优参数和性能评估
best_rf = grid_search.best_estimator_
y_pred = best_rf.predict(X_test)
print(f'Optimized Parameters: {grid_search.best_params_}')
print(f'Accuracy: {best_rf.score(X_test, y_test)}')

在这个例子中，我们使用`GridSearchCV`对随机森林模型中的树的数量和特征数量进行了优化，以期达到最优的模型性能。

### 2.5 支持向量机算法
#### 2.5.1 SVM的数学推导

支持向量机（SVM）是一种二分类模型，其基本模型定义为特征空间上间隔最大的线性分类器。在最简单的情况下，SVM使用一个超平面将两种类型的特征进行区分。其目标是找到一个超平面（决策边界）来最大化不同类别之间的间隔。

SVM通过使用核技巧能够处理非线性问题。核函数将原始数据映射到高维空间，使得原本在低维空间线性不可分的数据在高维空间变得线性可分。

#### 2.5.2 SVM在非线性问题中的应用

SVM在处理非线性问题时非常强大，它能在高维空间中找到最优的分割线（超平面）。尤其在文本分类和生物信息学等领域的高维数据处理中，SVM表现优异。

下面是一个使用`scikit-learn`库的`SVC`类的SVM模型实现示例：

from sklearn.svm import SVC
from sklearn.metrics import classification_report
from sklearn.model_selection import train_test_split

# 假设df是包含特征和目标变量的数据集
X = df.drop('target', axis=1)
y = df['target']

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化SVM模型
svm = SVC(kernel='linear')

# 训练模型
svm.fit(X_train, y_train)

# 预测测试集结果
y_pred = svm.predict(X_test)

# 输出分类报告评估模型性能
print(classification_report(y_test, y_pred))

在这段代码中，我们通过SVM模型对分类数据进行了训练和预测，并使用分类报告来评估了模型的性能，包括准确率、精确率、召回率以及F1分数。

以上就是第二章核心算法原理与实现的详细介绍。在接下来的章节中，我们将继续深入了解这些算法在不同领域的应用案例分析，从而更好地理解它们的工作机制和优化方式。

# 3. 算法应用案例分析

## 3.1 线性回归案例研究

### 3.1.1 数据准备与特征工程

线性回归是一种广泛使用的预测建模技术，用于分析两个或多个变量之间的关系。本案例将探讨如何使用线性回归模型对房屋销售价格进行预测。

在开始建模之前，需要进行详尽的数据准备和特征工程。首先，从房地产数据集中导入相关数据。数据应包括房屋的大小、卧室数量、浴室数量、楼层、房屋年龄、所在地区等特征。这些特征将作为独立变量（X），用于预测房屋的销售价格（y）。

在特征工程阶段，我们会对数据进行清洗，比如去除异常值、填充缺失值、处理分类变量以及标准化或归一化数值变量。以下是一个数据准备和特征工程的示例代码块：