支持向量机（SVM）：数据挖掘中的高级策略和应用


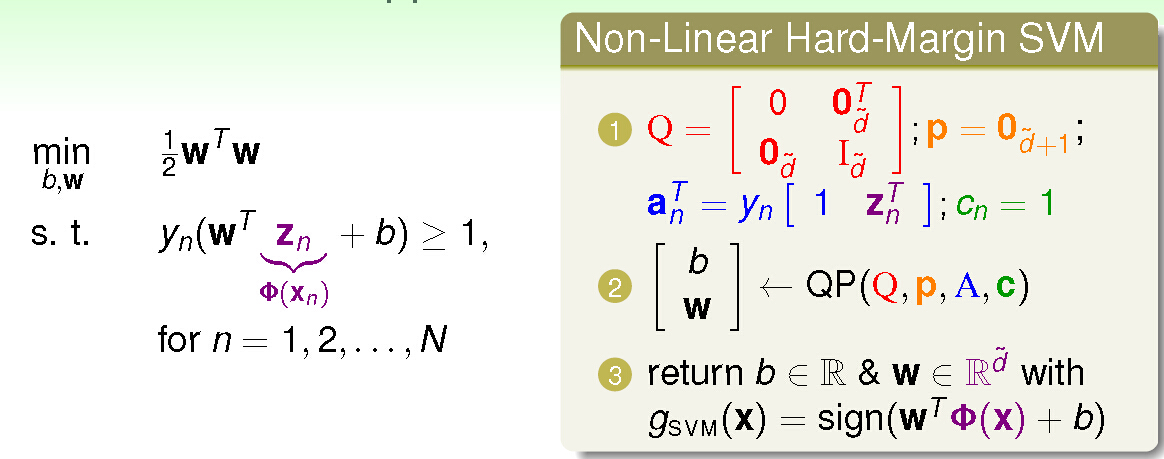
# 摘要
支持向量机（SVM）是一种广泛应用于模式识别和数据分类的机器学习方法。本文从理论基础入手，详细探讨了SVM模型的构建过程、参数优化以及性能评估。文中分析了不同数据集类型下SVM的应用策略，包括线性可分、线性不可分以及文本与高维数据集，并提供了多种优化策略和性能对比。进一步，本文深入讨论了SVM在图像识别、生物信息学和金融数据分析等实际问题中的应用，并对多类分类问题、在线学习以及SVM与其他机器学习方法的融合进行了探讨。最后，通过案例研究与实战演练，本文展现了SVM在特定行业中的应用，并提供了项目规划与执行的实战经验。整篇论文旨在为读者提供全面的SVM应用指南，并对未来的研究趋势做出展望。

# 关键字
支持向量机；模型构建；参数优化；性能评估；实际应用；案例研究

参考资源链接：[数据挖掘基础：陈封能等著《数据挖掘导论》英文第2版概览](https://wenku.csdn.net/doc/6tackw99ap?spm=1055.2635.3001.10343)
# 1. 支持向量机（SVM）的理论基础

支持向量机（SVM）是一种广泛应用于分类和回归分析的监督学习模型。在本章中，我们将探索SVM的核心概念和理论基础，为后续章节中模型的构建、优化及应用打下坚实的基础。

## 1.1 SVM的基本原理

SVM的主要思想是找到一个最优超平面，使得各类样本之间的间隔最大化。这一思想被称为最大间隔分类器，它通过最大化不同类别数据点间的边界来提高模型的泛化能力。具体来说，对于线性可分数据，SVM通过解决一个凸二次规划问题来得到最优超平面。对于线性不可分数据，引入核技巧将数据映射到更高维空间中，从而实现线性划分。

## 1.2 SVM的工作机制

SVM工作机制中，关键的组成部分是支持向量，它们是距离决策边界最近的点，对确定超平面起着决定性作用。SVM利用这些支持向量来构建分类边界，从而对新的数据点进行分类。在优化过程中，SVM通过软间隔最大化来允许一些数据点违反间隔约束，从而增强模型对噪声的容忍能力。

% 示例代码，展示SVM在二维空间线性分类中的应用
(* SVM Example Code Snippet *)
data = {{-1, 2}, {0, 1}, {1, 0}, {2, -1}};
labels = {-1, -1, 1, 1};
(* 使用支持向量机库进行训练 *)
model = SVMTrain[#, labels] &@data;
(* 可视化决策边界 *)
Show[{
  ListPlot[data, PlotStyle -> labels],
  Plot[SVMPredict[model, {x, y}], {x, -3, 3}, {y, -3, 3}]
}]

在上述伪代码中，我们展示了如何使用支持向量机进行二维空间中的数据分类。首先，我们创建了一组简单的二维数据集，并对其进行了标记。然后，我们训练了一个SVM模型，并使用该模型预测了一个决策边界，最后将决策边界和原始数据点进行了可视化展示。

本章为理解SVM的理论基础提供了初步的介绍和分析，下一章我们将进一步探讨SVM模型的构建与优化方法，深入到SVM的实际应用和案例分析中。

# 2. SVM模型的构建与优化

在第一章中，我们了解了支持向量机（SVM）的基本理论，接下来我们将深入探讨如何构建和优化SVM模型，以适应不同的应用场景和数据集。SVM模型的构建包括理解线性和非线性SVM的原理，以及使用核技巧将线性分类器扩展到非线性问题。参数调优是提高SVM性能的关键步骤，本章将详细讨论超参数的作用，以及如何使用网格搜索和交叉验证进行调优。性能评估对于验证模型的预测能力至关重要，我们将探索不同的评估指标和模型选择方法。

## 2.1 SVM模型构建

### 2.1.1 线性SVM的原理与构建

线性SVM是处理线性可分数据集的基本方法。在最简单的情况下，SVM通过找到一个超平面，将不同类别的数据点分隔开来，使得两个类别之间的间隔最大化。这种情况下，间隔是定义为最近的异类数据点到超平面的距离。数学上，可以通过求解以下优化问题来找到这个最优超平面：

\begin{aligned}
\min_{w,b} \quad & \frac{1}{2} ||w||^2 \\
\text{s.t.} \quad & y_i(w \cdot x_i + b) \geq 1, \quad i=1,\dots,n
\end{aligned}

其中，\(w\) 是超平面的法向量，\(b\) 是偏置项，\(x_i\) 和 \(y_i\) 分别表示数据点和它们的类别标签。

在Python中，可以使用scikit-learn库中的SVC类来构建线性SVM模型：

from sklearn.svm import SVC
from sklearn.datasets import make_classification

# 创建一个简单的线性可分数据集
X, y = make_classification(n_samples=100, n_features=2, n_redundant=0, n_clusters_per_class=1)

# 使用线性核初始化SVM模型
model = SVC(kernel='linear', C=1.0)
model.fit(X, y)

# 对数据集进行预测
predictions = model.predict(X)

上述代码段创建了一个线性可分数据集，并使用scikit-learn的SVC类构建了一个线性SVM模型。该模型使用线性核函数，意味着它直接应用在原始数据上进行分类。超参数`C`控制了模型对违反间隔约束的样本的容忍度，`C`值越大，模型对错误分类的惩罚就越严厉。

### 2.1.2 核技巧与非线性SVM

对于线性不可分的数据集，核技巧允许我们使用高维特征空间中的线性模型。核函数隐式地在高维空间中计算点积，而无需实际将数据映射到那个空间。常见的核函数包括多项式核、径向基函数（RBF）核和sigmoid核。

以RBF核为例，它能够将原始数据映射到一个无限维空间，从而实现非线性分类：

K(x_i, x_j) = \exp(-\gamma ||x_i - x_j||^2)

其中，\(\gamma\) 是一个超参数，它决定了数据映射到高维空间后的分布形状。

使用scikit-learn构建非线性SVM模型的代码如下：

from sklearn.datasets import make_circles
import numpy as np
import matplotlib.pyplot as plt

# 创建一个非线性可分数据集
X, y = make_circles(n_samples=100, factor=0.1, noise=0.1)

# 使用RBF核初始化SVM模型
model = SVC(kernel='rbf', gamma=10, C=1.0)
model.fit(X, y)

# 绘制决策边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, alpha=0.8)
plt.show()

在这个例子中，我们使用了`make_circles`函数创建了一个典型的非线性可分数据集，并使用了RBF核的SVM模型。模型超参数`gamma`和`C`被设置为1.0，`gamma`决定了数据映射到高维空间的密度。

## 2.2 SVM模型的参数调优

### 2.2.1 超参数的作用与选择

SVM模型的性能在很大程度上依赖于超参数的设置。超参数的调整是机器学习中最重要的步骤之一，它直接影响到模型的泛化能力。对于SVM来说，主要的超参数包括：

- C：正则化参数，控制了模型的复杂度和对错误分类的容忍度。
- gamma：RBF核函数的参数，控制了数据映射到高维空间的密度。
- kernel：核函数的选择，如线性核、多项式核、RBF核和sigmoid核。

超参数的选择需要通过实验来进行，常见的方法包括网格搜索和随机搜索。

### 2.2.2 调优方法：网格搜索与交叉验证

网格搜索是一种彻底的搜索策略，它遍历指定的参数组合来找到最佳的模型配置。交叉验证是一种评估模型泛化能力的技术，它将数据集分成k个子集，轮流将其中一个子集作为验证集，其余的作为训练集。

在scikit-learn中，可以结合使用`GridSearchCV`进行网格搜索和交叉验证：

from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC

# 定义参数网格
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': [1, 0.1, 0.01, 0.001],
    'kernel': ['rbf']
}

# 使用网格搜索和交叉验证
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=2)
grid.fit(X, y)

# 输出最佳参数和得分
print("Best parameters found: ", grid.best_params_)
print("Best cross-validated score: {:.2f}".format(grid.best_score_))

上述代码展示了如何使用`GridSearchCV`来找到最佳的超参数组合。在参数网格`param_grid`中，我们列出了不同的`C`值、`gamma`值和核函数`rbf`。`GridSearchCV`会评估所有可能的参数组合，并使用交叉验证来评估模型性能。

## 2.3 SVM模型的性能评估

### 2.3.1 模型评估指标

评估SVM模型性能时，常用的指标包括准确度、精确度、召回率、F1分数和ROC曲线。在二分类问题中，准确度是预测正确的样本比例。精确度指的是正确预测为正类别的样本比例，而召回率是实际为正类别且被正确预测的样本比例。

在多分类问题中，可以使用混淆矩阵来评估模型性能，它展示了不同类别之间的预测情况。

### 2.3.2 模型选择与比较

在选择最佳模型时，需要考虑不同评估指标的平衡。例如，在不平衡数据集中，精确度和召回率之间可能存在冲突。在这些情况下，F1分数（精确度和召回率的调和平均数）是一个有用的指标。ROC曲线（接收者操作特征曲线）和其下的面积（AUC）可用于比较模型在不同分类阈值下的性能。

评估模型时，可以使用scikit-learn中的`classification_report`和`plot_roc_curve`来帮助我们：

from sklearn.metrics import classification_report, plot_roc_curve
import seaborn as sns

# 使用网格搜索找到的最佳模型进行预测
best_model = grid.best_estimator_
y_pred = best_model.predict(X_test)

# 打印分类报告
print(classification_report(y_test, y_pred))

# 绘制ROC曲线
plot_roc_curve(best_model, X_test, y_test)
plt.show()

上述代码使用了`classification_report`来打印一个分类模型的综合报告，并使用`plot_roc_curve`绘制ROC曲线，评估模型在不同阈值下的表现。

通过上述章节内容的介绍，我们已经全面了解了SVM模型构建的基本原理、参数调优的方法和性能评估的重要性。接下来的章节将探讨SVM在不同类型数据集上的应用，以及在实际问题中的深入应用，包括图像识别、生物信息学和金融数据分析等。此外，还会涉及SVM的高级主题和未来趋势，以及案例研究与实战演练，帮助读者进一步掌握SVM的实战技能。

# 3. SVM在不同类型数据集上的应用

支持向量机（SVM）是一种强大的监督式学习模型，广泛应用于分类和回归问题。本章我们将深入探讨SVM在不同类型数据集上的具体应用，并分析在实际使用过程中如何根据数据集特性进行优化和改进。

## 3.1 线性可分数据集

在处理线性可分数据集时，SVM通过构建一个超平面将数据正确分类。我们将首先探讨如何在手写数字识别任务中应用线性SVM，并分析优化策略和性能对比。

### 3.1.1