MATLAB数据分类算法：从基础到高级技术

# 1. MATLAB数据分类算法概述

数据分类是机器学习中的一项核心技术，旨在将数据分组成不同的类别或簇。在MATLAB环境中，这一过程可以高效地完成，得益于它丰富而强大的数据分析和机器学习工具箱。本章将概述MATLAB如何支持各种数据分类任务，并简要介绍其在数据分析领域的重要性。

## 1.1 数据分类的定义与重要性

数据分类的核心目的是通过识别输入数据的模式，将数据映射到已知的分类中。这种技术广泛应用于从医疗诊断到欺诈检测的各个领域。MATLAB提供了一系列工具和函数，能够帮助数据科学家和工程师快速实现和测试分类模型。

## 1.2 MATLAB中的数据分类工具

MATLAB的机器学习工具箱包含了执行分类任务所需的所有组件。包括监督学习算法，如支持向量机（SVM）、决策树、神经网络等，以及无监督学习算法，例如K-均值聚类。用户可以通过编程或交互式界面使用这些工具，并且可以导入和处理各种格式的数据集，进行特征选择和模型训练，最终对新的数据进行准确分类。

在后续章节中，我们将深入探讨每一种分类技术，并通过示例和案例学习如何在MATLAB中应用这些技术。现在，让我们从基础分类技术开始我们的探索之旅。

# 2. 基础分类技术

MATLAB提供了丰富的工具和函数库，支持多种基础和高级的分类技术。在本章中，我们将深入探讨这些技术，并分析它们的内部工作机制、应用领域以及如何在MATLAB中实现它们。

## 2.1 线性分类器

线性分类器是数据分类中最简单、最直接的方法之一。它尝试找到一个线性边界，将不同类别的数据点分开。在本小节中，我们将重点关注两种线性分类器：线性判别分析（LDA）和逻辑回归与朴素贝叶斯分类。

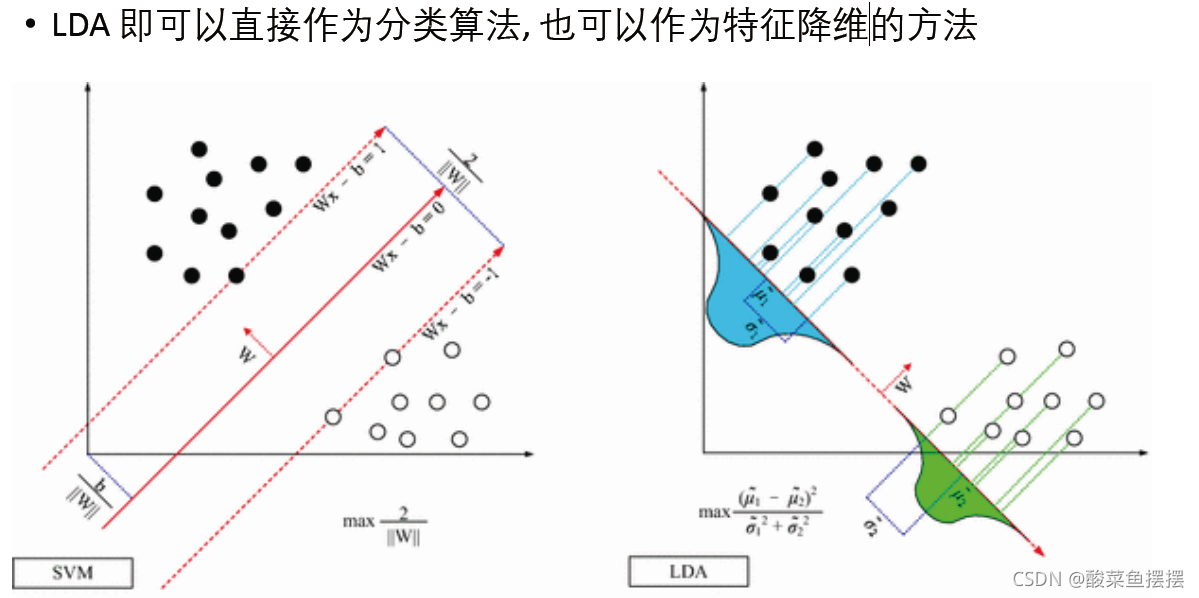
### 2.1.1 线性判别分析（LDA）

线性判别分析（LDA）是一种监督学习方法，用于分类和维度降低。LDA通过寻找最能区分数据的投影方向，将数据投影到较低维度的空间中。

**LDA的数学原理：**
LDA的目标是在投影后的数据中最大化类间距离，同时最小化类内距离。其目标函数可以表示为：

![LDA目标函数](***

其中，`\(S_b\)`是类间散度矩阵，`\(S_w\)`是类内散度矩阵。

**LDA的MATLAB实现：**
在MATLAB中，您可以使用内置函数`fitcdiscr`来实现LDA。例如：

load fisheriris
ldaModel = fitcdiscr(meas, species);

这将创建一个LDA模型`ldaModel`，用于根据测量值预测鸢尾花的种类。

### 2.1.2 逻辑回归与朴素贝叶斯分类

逻辑回归是一种广泛用于二分类问题的统计方法，它使用逻辑函数来预测属于某个特定类别的概率。朴素贝叶斯分类器则是一种基于贝叶斯定理的简单概率分类器，它假设特征之间相互独立。

**逻辑回归的MATLAB实现：**

% 逻辑回归
X = [ones(size(meas,1),1) meas]; % 添加截距项
y = species == 'setosa'; % 二分类问题
b = X\y'; % 解线性方程组得到参数

**朴素贝叶斯分类器的MATLAB实现：**

% 朴素贝叶斯
nbModel = fitcnb(meas, species);

朴素贝叶斯模型通过`fitcnb`函数创建。一旦模型被训练，你就可以用它来预测新的测量值。

## 2.2 k-最近邻（k-NN）算法

k-NN算法是一种基本的分类和回归方法。在分类问题中，输出是基于对象与最近邻的类别。

### 2.2.1 k-NN原理与实现

k-NN算法的原理基于一个假设，即相似的数据点往往属于同一个类别。在MATLAB中，可以使用`fitcknn`函数来创建k-NN分类器。

**k-NN的MATLAB实现：**

knnModel = fitcknn(meas, species, 'NumNeighbors', 3);

在这里，`NumNeighbors`参数用于指定邻居的数量`k`。

### 2.2.2 距离度量与权重选择

距离度量通常用于确定数据点之间的“最近”距离。欧氏距离是最常用的度量方法，但其他度量方法如曼哈顿距离、切比雪夫距离和马氏距离在特定情况下也可能是更好的选择。

% 曼哈顿距离
distances = pdist2(meas, queryPoint, 'cityblock');

此外，距离权重也可以用作k-NN算法的改进，通过给予距离近的邻居更高的权重来提高预测的精度。

## 2.3 支持向量机（SVM）

支持向量机（SVM）是一种强大的分类方法，主要用于线性和非线性分类问题。

### 2.3.1 SVM基本概念和原理

SVM通过找到一个超平面来对数据进行分类，该超平面最大化了不同类别数据点之间的间隔。

**SVM的MATLAB实现：**

svmModel = fitcsvm(meas, species);

### 2.3.2 核技巧与软间隔优化

当数据不是线性可分的时候，核技巧可以用来将数据映射到高维空间，这样在新空间中数据就变得线性可分了。在MATLAB中，可以通过指定核函数来使用核技巧。

% 使用高斯核
svmModel = fitcsvm(meas, species, 'KernelFunction', 'RBF', 'KernelScale', 'auto');

在实际应用中，软间隔优化方法允许一些分类错误，以提高模型的泛化能力。

在本章中，我们详细介绍了MATLAB中三种基础分类技术的原理和实现方式。这些技术为更复杂的分类方法打下了坚实的基础。接下来，在第三章中，我们将继续探索高级分类技术，并进一步了解如何在MATLAB中应用这些技术。

# 3. 高级分类技术

随着数据科学和机器学习的发展，高级分类技术在解决复杂问题方面变得越来越重要。本章将探讨决策树与集成方法、神经网络分类器和高斯过程分类器，并深入理解这些技术背后的原理和应用。

## 3.1 决策树与集成方法

决策树是一种流行的机器学习模型，它通过一系列的问题来对数据进行分类。而集成方法，如随机森林和梯度提升机，通过构建多个决策树并将它们的预测结果组合起来，以提高模型的整体性能。

### 3.1.1 决策树构造与剪枝

决策树的构造过程涉及递归地选择最优的特征进行分割。这个过程不断地重复，直到满足停止条件，例如树达到最大深度或者分支节点中的样本数小于某个阈值。

剪枝是决策树训练过程中的重要步骤，它通过减少树的复杂度来防止过拟合。剪枝可以发生在构造树的过程中（预剪枝），或者构造完成后（后剪枝）。

graph TD;
    A[开始训练决策树] --> B[选择最佳分割特征];
    B --> C[构建节点];
    C --> D{是否满足停止条件?};
    D -- 是 --> E[停止分割，形成叶节点];
    D -- 否 --> F[继续分割，创建分支];
    F --> B;
    E --> G{是否进行剪枝?};
    G -- 是 --> H[执行剪枝操作];
    G -- 否 --> I[结束训练];
    H --> I;

### 3.1.2 随机森林与梯度提升机

随机森林通过构建多个决策树并平均它们的预测结果来提升性能。每棵树都是在一个随机选取的训练子集上训练的，并且每次分割节点时只考虑一定数量的特征。

梯度提升机是一种集成学习技术，它通过迭代地添加树来最小化损失函数。在每一步中，新树都尝试纠正前一轮树的预测错误。

## 3.2 神经网络分类器

神经网络分类器是一类模仿生物神经网络结构和功能的算法。近年来，随着计算能力的提升和大数据的普及，深度学习在图像识别、语音处理、自然语言理解等领域取得了显著成功。

### 3.2.1 前馈神经网络基础

前馈神经网络是最简单的神经网络模型，其中的信息流是单向的，没有反馈循环。每一层的神经元仅与下一层的神经元相连，且不与同一层的神经元或更早层的神经元相连。

构建一个前馈神经网络需要确定网络的结构，包括层数、每层的神经元数目，以及激活函数的选择。

### 3.2.2 卷积神经网络（CNN）在分类中的应用

卷积神经网络是深度学习中用于图像识别和处理的热门网络结构。CNN通过卷积层来提取图像中的空间特征，通常还包含池化层来减少数据的维度，以及全连接层来进行分类。

graph LR;
    A[输入图像] --> B[卷积层];
    B --> C[激活函数];
    C --> D[池化层];
    D --> E[ Flatten层];
    E --> F[全连接层];
    F --> G[输出分类结果];

在构建CNN模型时，需要仔细设计卷积核的大小、数量，池化窗口的大小，以及全连接层的神经元数目。

## 3.3 高斯过程分类器

高斯过程是一种基于概率的机器学习方法，它适用于回归和分类问题。高斯过程分类器利用训练数据的分布特性来进行预测，能够给出预测的置信区间。

### 3.3.1 高斯过程的基本理论

高斯过程是通过一个无限维的高斯分布来表示随机变量的集合。在分类问题中，高斯过程可以用来估计不同类别的概率分布。

高斯过程的预测不依赖于固定的模型参数，而是依赖于训练数据。因此，它是一种非参数化的方法。

### 3.3.2 超参数优化与分类应用实例

高斯过程分类器的性能很大程度上取决于超参数的选择。常用的超参数包括核函数的类型和参数，以及噪声方差等。

超参数优化通常采用最大化边缘似然的方法，也称为类型II最大似然估计。实际操作中，可以通过网格搜索、随机搜索或贝叶斯优化来进行。

from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF

# 创建高斯过程分类器实例，核函数使用径向基函数（RBF）
kernel = 1.0 * RBF(length_scale=1.0)
clf = GaussianProcessClassifier(kernel=kernel)

# 训练模型
clf.fit(X_train, y_train)

# 预测
y_pred, sigma = clf.predict(X_test, return_std=True)

在上述代码中，`GaussianProcessClassifier`类被用来创建高斯过程分类器实例，其中指定了RBF核函数，并通过`fit`方法在训练数据上进行训练，最后通过`predict`方法对测试数据进行分类预测。

在本章节中，我们探讨了决策树与集成方法、神经网络分类器和高斯过程分类器等高级分类技术。我们分析了这些技术的构建原理、训练过程以及实际应用。通过本章节的介绍，读者将能够理解并应用这些高级技术来解决实际问题。

# 4. 数据预处理与特征选择

在数据科学领域，数据预处理和特征选择是构建有效模型的两个关键步骤。通过这两个步骤，我们能够将原始数据转换为干净、有用且易于模型处理的格式。本章节将深入探讨数据预处理与特征选择的理论和实践，从而为读者提供一个全面的理解和应用指导。

## 数据清洗与标准化

数据预处理的第一步是数据清洗，其目标是识别并纠正数据中的错误或不一致性。接下来是数据标准化，这涉及到将数据转换为统一的格式，以消除不同尺度或分布的影响。

### 缺失值处理与异常值检测

在数据集中，缺失值和异常值是常见的问