高级天线分析:HFSS中参数扫描与优化技术的专业指南
发布时间: 2024-12-03 06:37:02 阅读量: 73 订阅数: 49 


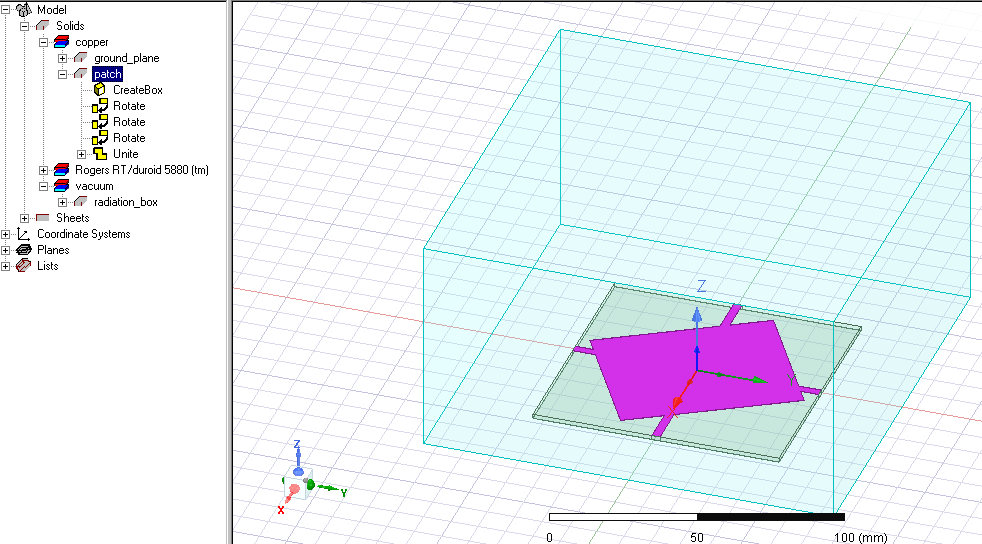
MATLAB与HFSS联合建模与仿真优化详细介绍
参考资源链接:[使用HFSS进行雷达截面(RCS)计算教程](https://wenku.csdn.net/doc/55nffgpm5f?spm=1055.2635.3001.10343)
# 1. HFSS参数扫描与优化技术概述
在现代电子设计自动化(EDA)领域中,HFSS(High Frequency Structure Simulator)作为一种全波电磁场仿真软件,广泛应用于复杂电磁问题的模拟与分析。随着技术的发展,参数扫描与优化技术已成为HFSS中的核心功能,它们使工程师能够对产品设计进行深入分析,快速定位最佳设计方案。
参数扫描技术允许用户在指定范围内改变一个或多个设计变量,进而观察设计性能的变化趋势。通过系统性地调整这些参数,可以全面理解设计参数与性能指标之间的关系,为设计决策提供数据支撑。
优化技术则是基于参数扫描的进一步应用,它通过自动迭代搜索,寻找到满足预设目标函数和约束条件的设计参数组合。在HFSS中,利用优化技术可以实现设计的自动化改进,不仅显著提高设计效率,也优化了最终产品的性能。
# 2. HFSS参数扫描基础
### 2.1 参数扫描的基本概念
#### 2.1.1 参数扫描的定义和作用
参数扫描在工程设计和数值仿真中占据着举足轻重的地位。它允许工程师对一个或多个设计参数进行系统的改变,以研究这些参数变化对整个系统性能的影响。在HFSS(High-Frequency Structure Simulator)中,参数扫描可以用于分析天线、微波器件等高频结构的频率响应、电磁场分布、S参数等关键性能指标随参数变化的情况。定义好参数扫描可以揭示设计的敏感性,预测设计在不同条件下的表现,以及为优化设计提供基础数据。
#### 2.1.2 参数扫描的类型及其应用场景
HFSS提供的参数扫描类型有多种,包括线性扫描、对数扫描、列表扫描和蒙特卡罗扫描等。线性扫描适用于参数变化范围均匀且已知的情况,而对数扫描通常用于频率等需要对数刻度的变化参数。列表扫描提供了一种灵活的方式来指定不规则的参数值,适用于某些特定的实验设计。蒙特卡罗扫描则适用于不确定性分析和随机变量的影响评估,它通过随机抽样生成参数值,模拟现实世界的复杂性。
### 2.2 参数扫描的设置方法
#### 2.2.1 参数的创建与管理
在HFSS中创建参数,首先需要在项目树中的“Design Setting”下打开参数窗口,然后通过“Add Parameter”按钮添加新的参数。参数的命名应具有描述性,以便于理解和管理。创建参数后,可以设置参数的初始值、范围、单位等属性。参数的管理还包括复制、修改、删除等操作,需要通过参数窗口的相关选项进行。
```mermaid
graph TD;
A[开始参数设置] --> B[打开Design Setting];
B --> C[点击Add Parameter];
C --> D[输入参数名称和初始值];
D --> E[设置参数范围和单位];
E --> F[完成参数创建];
F --> G[进行参数复制、修改和删除];
```
#### 2.2.2 扫描任务的配置与执行
配置参数扫描任务通常包括选择扫描类型、定义扫描范围以及设置扫描的步长或样本数。在HFSS中,扫描任务的配置是在“Analysis”菜单下的“Parametric”选项中完成的。执行扫描任务前,需要选择分析类型(如S参数、天线增益等)并设置所需的仿真类型(如谐波平衡、时域等)。执行参数扫描后,HFSS会根据定义的参数集自动运行多个仿真案例,并收集结果以供分析。
```mermaid
graph TD;
A[开始配置扫描] --> B[选择扫描类型];
B --> C[定义参数扫描范围和步长];
C --> D[设置分析类型];
D --> E[设置仿真类型];
E --> F[开始执行参数扫描];
F --> G[HFSS运行多个仿真案例];
G --> H[收集仿真结果];
```
### 2.3 参数扫描的结果分析
#### 2.3.1 结果数据的获取与管理
HFSS仿真完成后,结果数据通常以*.db或*.sNp格式存储。这些数据包含了仿真的全部结果,可以通过HFSS的后处理工具进行分析和可视化。结果数据的获取包括读取仿真结果文件、导出特定数据点或曲线等步骤。结果数据的管理则需要在仿真项目中建立合理的文件结构和命名规则,以便于后期查找和调用。
```mermaid
graph TD;
A[开始结果分析] --> B[打开仿真结果文件];
B --> C[读取所需仿真数据];
C --> D[导出数据点或曲线];
D --> E[建立文件结构和命名规则];
E --> F[后期数据调用和分析];
```
#### 2.3.2 结果数据的可视化处理
为了更直观地理解参数变化对系统性能的影响,结果数据需要通过图表、表面图、等值线图等可视化手段进行处理。HFSS提供了强大的后处理工具,可以帮助用户绘制各类图表。在数据可视化过程中,关键步骤包括选择合适的数据类型、设定图形的坐标轴和视图参数、应用不同的颜色方案和阴影效果以及添加必要的注释和标题。经过精心设计的可视化图表不仅能够清楚地展示数据信息,而且有助于识别和分析参数与性能指标之间的关系。
```mermaid
graph TD;
A[开始数据可视化] --> B[选择数据类型];
B --> C[设置图形坐标轴和视图参数];
C --> D[应用颜色方案和阴影效果];
D --> E[添加注释和标题];
E --> F[分析参数与性能指标关系];
```
通过以上介绍的参数扫描基础,我们能够开始在HFSS中进行初步的参数扫描和结果分析。接下来的章节将深入探讨如何在HFSS中运用优化技术,进一步提升设计的质量和性能。
# 3. HFSS中的优化技术
## 3.1 优化技术的基本原理
### 3.1.1 优化问题的数学模型
优化问题通常可以通过定义一个目标函数来表示,目标函数衡量了设计变量在特定约束条件下的性能指标。在HFSS中,这涉及到定义一个设计空间,其可能包括几何参数、材料属性以及边界条件等。目标函数则通常是电性能参数,如增益、驻波比、带宽等。优化算法将搜索该设计空间,寻找使目标函数达到预定最佳值的设计变量组合。
在数学模型中,优化问题可以表达为:
```
minimize/maximize f(x)
subject to gi(x) ≤ 0, i=1,2,...,m
hj(x) = 0, j=1,2,...,p
```
其中,`f(x)`是目标函数,`gi(x) ≤ 0`是不等式约束条件,`hj(x) = 0`是等式约束条件,而`x`代表设计变量向量。
### 3.1.2 优化算法的分类和选择
根据不同的优化目标和设计变量的特性,可以选用不同的优化算法。常见的优化算法包括梯度下降法、遗传算法、粒子群优化等。这些算法各有优劣,适用于不同类型的问题。
- **梯度下降法**:适用于连续可导的目标函数,算法易于实现,但在非凸问题或梯度信息不易获取的情况下效果不佳。
- **遗传算法**:一种模拟自然选择
0
0





