掌握MATLAB数值计算进阶：解锁数值计算的奥秘，解决复杂问题

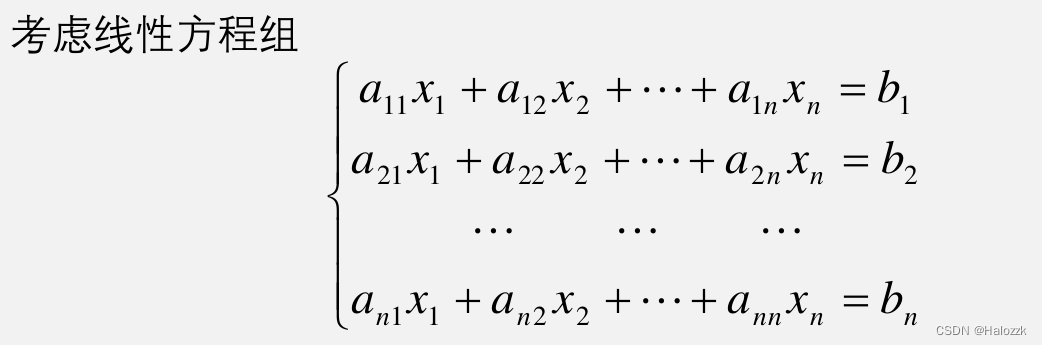
# 1. MATLAB数值计算基础**

MATLAB是一种用于数值计算和数据分析的高级编程语言。它提供了一系列强大的函数和工具箱，使您可以轻松解决各种科学和工程问题。

MATLAB的核心优势之一是其矩阵操作能力。它允许您轻松处理和操作大型矩阵，这对于数值计算至关重要。MATLAB还提供了一系列用于求解线性方程组、执行数值积分和微分以及优化算法的函数。

这些基础功能为更高级的数值计算技术奠定了基础，例如图像处理、信号处理和数据分析。MATLAB在这些领域提供了丰富的工具箱，使您可以轻松高效地执行复杂的任务。

# 2. 数值计算技术

**2.1 线性代数**

### 2.1.1 矩阵操作

MATLAB提供了丰富的矩阵操作函数，包括：

- **矩阵创建：**zeros、ones、eye、rand、randn
- **矩阵运算：**+, -, *, /、.^（幂运算）、inv（求逆）
- **矩阵分解：**eig（求特征值和特征向量）、svd（奇异值分解）
- **矩阵求解：**rref（行阶梯形）、lu（LU分解）、chol（Cholesky分解）

**代码块：**

% 创建一个 3x3 单位矩阵
A = eye(3);

% 计算矩阵 A 的逆
A_inv = inv(A);

% 计算矩阵 A 的特征值和特征向量
[V, D] = eig(A);

**逻辑分析：**

* `eye(3)` 创建一个 3x3 单位矩阵，对角线元素为 1，其他元素为 0。
* `inv(A)` 计算矩阵 A 的逆，如果 A 是可逆的，则返回其逆矩阵。
* `eig(A)` 计算矩阵 A 的特征值和特征向量。`V` 为特征向量矩阵，`D` 为特征值对角矩阵。

### 2.1.2 求解线性方程组

MATLAB提供了多种求解线性方程组的方法：

- **直接法：**\（左除）、inv（求逆）
- **迭代法：**gmres、bicgstab、pcg

**代码块：**

% 创建一个系数矩阵和右端向量
A = [2 1; 3 4];
b = [5; 7];

% 使用左除求解线性方程组
x1 = A \ b;

% 使用求逆求解线性方程组
x2 = inv(A) * b;

**逻辑分析：**

* `A \ b` 使用左除运算符求解线性方程组 Ax = b。
* `inv(A) * b` 使用求逆运算符求解线性方程组 Ax = b。

**表格：线性代数函数对比**

| 函数 | 功能 | 优点 | 缺点 |
|---|---|---|---|
| zeros | 创建零矩阵 | 创建速度快 | 存储空间消耗大 |
| ones | 创建单位矩阵 | 创建速度快 | 存储空间消耗大 |
| eye | 创建单位矩阵 | 创建速度快 | 存储空间消耗大 |
| rand | 创建随机矩阵 | 创建速度快 | 随机性可能影响结果 |
| randn | 创建正态分布随机矩阵 | 创建速度较慢 | 随机性可能影响结果 |
| + | 矩阵加法 | 计算速度快 | 矩阵维度必须一致 |
| - | 矩阵减法 | 计算速度快 | 矩阵维度必须一致 |
| * | 矩阵乘法 | 计算速度较慢 | 矩阵维度必须满足乘法规则 |
| / | 矩阵除法 | 计算速度较慢 | 矩阵必须可逆 |
| .^ | 矩阵幂运算 | 计算速度较慢 | 矩阵必须为方阵 |
| inv | 矩阵求逆 | 计算速度较慢 | 矩阵必须可逆 |
| eig | 矩阵特征值和特征向量 | 计算速度较慢 | 矩阵必须为方阵 |
| svd | 矩阵奇异值分解 | 计算速度较慢 | 矩阵必须为方阵 |
| rref | 矩阵行阶梯形 | 计算速度较慢 | 矩阵必须为方阵 |
| lu | 矩阵 LU 分解 | 计算速度较慢 | 矩阵必须为方阵 |
| chol | 矩阵 Cholesky 分解 | 计算速度较慢 | 矩阵必须为正定对称矩阵 |
| \ | 矩阵左除 | 计算速度较慢 | 矩阵必须可逆 |
| gmres | 矩阵迭代求解器 | 计算速度较慢 | 适用于大型稀疏矩阵 |
| bicgstab | 矩阵迭代求解器 | 计算速度较慢 | 适用于大型对称正定矩阵 |
| pcg | 矩阵迭代求解器 | 计算速度较慢 | 适用于大型