探索MATLAB数值计算的强大力量：数值计算的艺术与科学

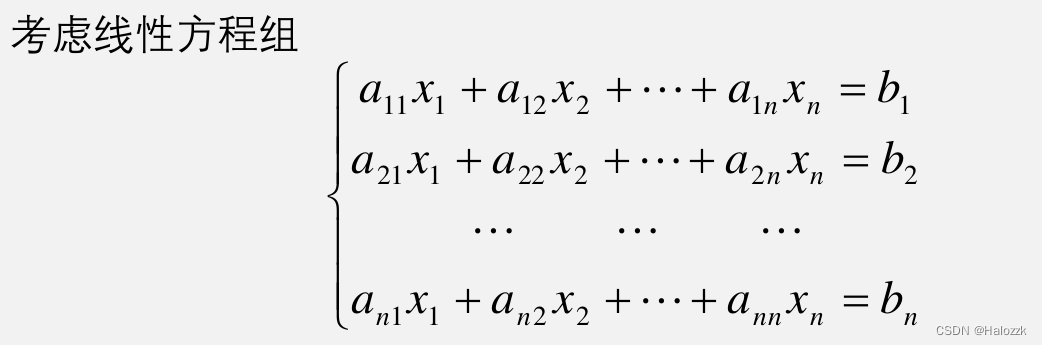
# 1. MATLAB概述

MATLAB（Matrix Laboratory）是一种强大的技术计算环境，用于数值计算、数据分析和可视化。它由MathWorks公司开发，广泛应用于工程、科学、金融和数据科学等领域。MATLAB以其交互式环境、丰富的函数库和易于使用的语法而著称。

MATLAB的核心优势之一在于其对矩阵操作的强大支持。它提供了广泛的矩阵函数，可以高效地执行各种线性代数运算，例如矩阵乘法、求逆和特征值计算。此外，MATLAB还提供了丰富的工具箱，用于解决特定领域的复杂问题，例如信号处理、图像处理和机器学习。

# 2. 数值计算的基础

### 2.1 数值表示和精度

在MATLAB中，数值使用浮点数表示，这是一种近似表示实数的方法。浮点数由三个部分组成：

- 符号（+或-）：表示数字的正负。
- 尾数（小数部分）：表示数字的有效数字。
- 指数（幂）：表示尾数乘以的10的幂。

例如，数字123.456789可以表示为：

+1.23456789e+02

其中：

- 符号为+，表示数字为正。
- 尾数为1.23456789。
- 指数为+02，表示尾数乘以10的2次方。

MATLAB中的浮点数精度受计算机体系结构和浮点数表示格式的影响。IEEE 754标准定义了两种常见的浮点数格式：

- 单精度（float）：32位，尾数精度为24位，指数范围为[-126, 127]。
- 双精度（double）：64位，尾数精度为53位，指数范围为[-1022, 1023]。

### 2.2 误差分析和数值稳定性

在数值计算中，由于浮点数表示的近似性，可能会产生误差。误差可以分为以下几类：

- **舍入误差：**将无限小数转换为有限小数时产生的误差。
- **截断误差：**当算法使用有限数量的步骤近似连续过程时产生的误差。
- **算法误差：**算法本身固有的误差。

误差分析涉及研究和量化这些误差，以确保计算结果的准确性。数值稳定性是指算法对输入数据和计算过程中的小扰动不敏感的能力。

为了提高数值稳定性，可以使用以下技术：

- **条件数：**测量算法对输入扰动的敏感性。
- **正则化：**通过重新表述问题来减少条件数。
- **迭代精化：**使用迭代方法逐步提高结果的精度。

# 3.1 矩阵操作和线性方程组求解

**矩阵操作**

MATLAB 提供了丰富的矩阵操作功能，包括矩阵创建、索引、算