【Outlier检测解析】：线性回归中离群值的发现与处理技巧

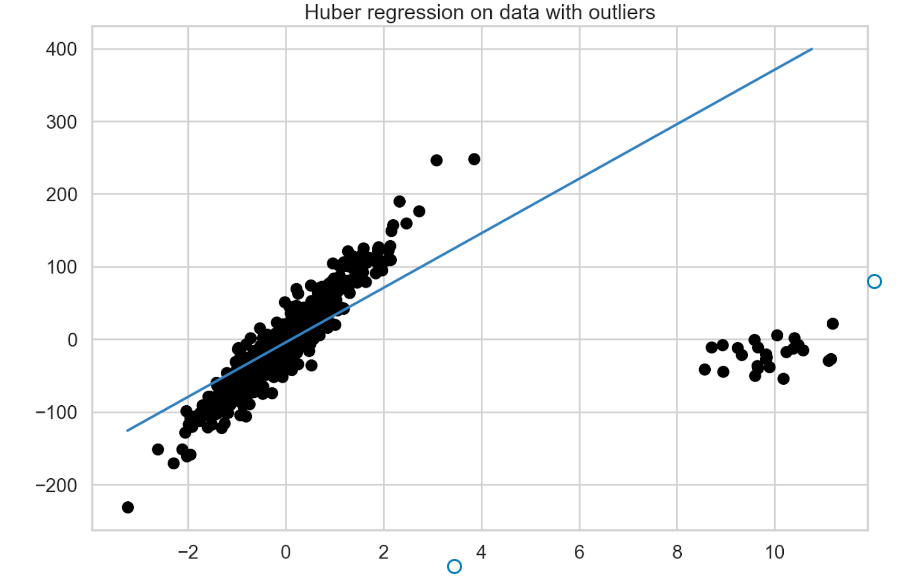
# 1. 介绍Outlier检测解析

在数据分析和机器学习中，离群值（Outlier）是指与大部分数据显著不同的数据点，可能由于测量错误、异常情况或真实特征而产生。离群值检测是数据预处理的重要步骤，其目标是识别和处理这些异常值，以确保建模过程的可靠性和准确性。本章将深入介绍离群值检测的概念、应用场景以及常用的方法，帮助读者全面了解离群值在数据分析中的重要性和处理方法。

# 2. 线性回归基础知识
线性回归是一种经典的机器学习方法，常被用来建立特征与目标之间的线性关系模型。在本章中，我们将深入了解线性回归的原理、优缺点以及应用领域。

### 2.1 什么是线性回归
#### 2.1.1 线性回归的原理
线性回归的核心思想是通过线性组合输入特征来预测输出值，其数学表达式为：$Y = βX + α$。
其中，$Y$ 是预测值，$X$ 是特征，$β$ 是特征的权重，$α$ 是偏置项。

#### 2.1.2 线性回归的优缺点
- 优点：简单易于理解和实现、计算代价低。
- 缺点：对于非线性数据拟合效果不佳、容易受离群值影响。

#### 2.1.3 线性回归的应用领域
线性回归广泛用于预测和建模，包括但不限于房价预测、销售趋势分析、股市波动预测等。

### 2.2 线性回归算法
线性回归算法主要包括最小二乘法、梯度下降法和正规方程法。

#### 2.2.1 最小二乘法
最小二乘法是通过最小化实际值与预测值的残差平方和来求解最优参数的方法。

import numpy as np
from sklearn.linear_model import LinearRegression

# 创建线性回归模型
model = LinearRegression()
# 拟合数据
model.fit(X, y)

// 输出模型参数
print(model.coef_, model.intercept_)

输出参数：[β1, β2, ..., βn] α

#### 2.2.2 梯度下降法
梯度下降法是一种迭代优化算法，通过迭代更新参数以最小化损失函数。

# 初始化参数
weights = np.zeros(X.shape[1])
bias = 0
# 梯度下降迭代
for i in range(num_iterations):
# 计算梯度
grad = compute_gradient(X, y, weights, bias)
weights = weights - learning_rate * grad
bias = bias - learning_rate * np.sum(grad)

// 输出最优参数
print(weights, bias)

输出参数：[β1, β2, ..., βn] α

#### 2.2.3 正规方程法
正规方程法是通过求解闭式解来直接获得最优参数。

# 计算闭式解
theta = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y)

输出参数：[β1, β2, ..., βn] α

本章节详细介绍了线性回归的基础知识，包括原理、优缺点和常用算法。通过理解这些内容，可以更好地应用线性回归模型进行数据分析和预测。

# 3. 离群值检测方法

### 3.1 基于统计学方法的离群值检测
在数据分析领域，离群值是指与其他观测值明显不同的数值，可能由噪声、数据采集错误或某种特殊情况引起。基于统计学的离群值检测方法主要通过一些统计学上的指标来判断数据点是否为离群值。常见的统计学方法包括Z-Score方法和IQR方法。

#### 3.1.1 Z-Score方法
Z-Score方法是一种常用的离群值检测方法，它通过计算数据点与均值的偏差来判断数据点是否为离群值。具体步骤如下：

# 计算Z-Score
Z_score = (X - mean) / std
if Z_score > threshold:
    # 判断为离群值
    print("Outlier Detected using Z-Score method")

Z-Score方法的优点是简单易懂，适用于数据较为集中的情况，但对数据分布要求较高。

#### 3.1.2 IQR方法
IQR方法使用四分位距（Interquartile Range, IQR）来识别离群值，通过计算数据的上下四分位数来确定数据的分布情况，检测方法如下：

# 计算上下四分位数
Q1 = np.percentile(data, 25)
Q3 = np.percentile(data, 75)
IQR = Q3 - Q1

# 计算IQR离群值边界
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

if data < lower_bound or data > upper_bound:
    # 判断为离群值
    print("Outlier Detected using IQR method")

IQR方法相对稳健，适用于数据较为分散的情况，但对数据的分布要求不高。

### 3.2 基于距离的离群值检测
基于距离的离群值检测方法是利用数据点之间的距离来判断数据点是否为离群值。常见的方法包括K近邻方法和LOF方法。

#### 3.2.1 K近邻方法
K近邻方法通过计算数据点与其最近的K个邻居的距离来判断数据点是否为离群值，若数据点距离其邻居较远，则可能是离群值。具体步骤如下：

# 计算K个最近邻居的距离
distances = calculate_distances(data_point, neighbors)
if average_distance > threshold:
    # 判断为离群值
    print("Outlier Detected using KNN method")

#### 3.2.2 LOF(Local Outlier Factor) 方法
LOF方法是一种基于密度的离群值检测方法，通过计算数据点与其邻居之间的密度关系来判断数据点是否为离群值。LOF越大，表示数据点越有可能是离群值。具体步骤如下：

# 计算LOF
LOF = calculate_LOF(data_point, neighbors)
if LOF > threshold:
    # 判断为离群值
    print("Outlier Detected using LOF method")

### 3.3 基于密度的离群值检测
基于密度的离群值检测方法是根据数据点周围的密度来判断数据点是否为离群值的方法。常见的方法包括DBSCAN方法和HBOS方法。

#### 3.3.1 DBSCAN方法
DBSCAN是一种基于密度的聚类方法，可以用来识别离群值。它通过定义领域内最少数据点个数和领域内所有点的距离阈值来判断数据点是否为核心点、边界点或离群值。

#### 3.3.2 HBOS(Histogram-based Outlier Score) 方法
HBOS方法是一种基于直方图的离群值检测方法，它通过构建特征空间的直方图来度量数据点的异常程度。HBOS在处理大数据集时具有较高的效率和可扩展性。

通过本节介绍，我们了解了离群值检测的常用方法，包括基于统计学的方法、基于距离的方法和基于密度的方法。这些方法在实际数据分析中具有重要的应用意义，能帮助我们发现数据中的异常情况，并进行相应的处理。

# 4. 线性回归的离群值处理技巧

### 4.1 离群值对线性回归的影响

在进行线性回归分析时，离群值可能会对模型产生不良影响，导致模型的准确性下降，参数估计失真。离群值可能会使得回归系数偏离真实值，导致模型预测能力下降，增加模型的误差。因此，对离群值的处理至关重要。

### 4.2 离群值处理方法

在线性回归中，处理离群值是必不可少的环节。下面将介绍几种常用的离群值处理方法：

#### 4.2.1 删除离群值

删除离群值是最简单直接的方法之一。该方法适用于数据集中离群值较少且不影响整体数据分布的情况。通过识别离群值并将其剔除，可以使得模型更加准确。

# 删除离群值的代码示例
clean_data = original_data[(original_data['feature'] > lower_bound) & (original_data['feature'] < upper_bound)]

#### 4.2.2 替换离群值

替换离群值是另一种常见的处理方法，适用于离群值对整体数据分布影响不大的情况。可以通过均值、中位数或者其他合适的值来替换离群值，使得数据更加稳定。

# 替换离群值的代码示例
original_data.loc[original_data['feature'] > upper_bound, 'feature'] = median_value

#### 4.2.3 离群值转换

离群值转换是一种更为复杂的处理方法，可以对离群值进行转换，使得其更符合整体数据分布，降低其对模型的干扰程度。常见的转换方式包括取对数、平方根等。

# 离群值转换为中位数的代码示例
original_data['feature'] = np.where(original_data['feature'] > upper_bound, median_value, original_data['feature'])

通过以上处理方法，可以有效应对线性回归中的离群值问题，提高模型的稳定性和准确性。

### 表格示例：常见离群值处理方法比较

| 方法 | 适用场景 | 优点 | 缺点 |
| ---------- | ----------------------------------- | --------------------- | ------------------ |
| 删除离群值 | 离群值数量极少，不影响整体数据分布 | 简单，直接 | 可能丢失有效信息 |
| 替换离群值 | 离群值不多，对整体数据影响较小 | 可保留原始数据信息 | 可能引入新的误差 |
| 离群值转换 | 需要保留离群值，降低其影响程度 | 能保留原始数据特征 | 转换方法选择较为主观 |

以上是离群值处理技巧的简要介绍，根据具体情况选择合适的方法进行处理，可以提升数据分析的准确性和可靠性。

# 5. 案例分析

### 5.1 数据准备与探索性分析

在进行离群值检测和线性回归建模之前，首先需要进行数据准备和探索性分析。这个阶段是非常关键的，因为数据的质量将直接影响后续建模的效果。

首先，导入必要的库，并加载数据集：

import pandas as pd
import numpy as np

# 导入数据集
data = pd.read_csv('your_dataset.csv')

接着，我们可以查看数据集的基本信息，包括数据类型、缺失值情况等：

# 查看数据集基本信息
print(data.info())

# 查看数值型特征的统计信息
print(data.describe())

在掌握了数据的基本信息后，可以进行数据的可视化探索，比如绘制直方图、箱线图等，以便更好地理解数据分布和可能存在的离群值：

import matplotlib.pyplot as plt
import seaborn as sns

# 绘制数据分布直方图
plt.figure(figsize=(12, 6))
sns.histplot(data['feature'], bins=20, kde=True)
plt.title('Feature Distribution')
plt.show()

# 绘制箱线图
plt.figure(figsize=(8, 6))
sns.boxplot(x=data['feature'])
plt.title('Boxplot of Feature')
plt.show()

通过以上步骤，我们可以对数据进行初步的了解，为接下来的离群值检测和处理以及线性回归建模做好准备。

### 5.2 离群值检测

离群值检测是指识别出那些远离正常模式的数据点，可能会对建模结果产生负面影响的数据点。常见的离群值检测方法包括基于统计学、距离和密度的方法。

#### 5.2.1 Z-Score方法

Z-Score方法是基于数据的标准差和均值来判断数据点是否为离群值的一种方法。一般来说，绝对Z-Score大于3的数据点可以被认定为离群值。

下面是Z-Score方法的代码实现：

from scipy import stats

# 计算Z-Score
z_scores = np.abs(stats.zscore(data['feature']))

# 设置阈值
threshold = 3

# 判断离群值
outliers = data['feature'][z_scores > threshold]

print("Z-Score离群值数量：", outliers.shape[0])
print("离群值：\n", outliers)

#### 5.2.2 IQR方法

IQR方法利用四分位数来确定数据的异常值。异常值通常定义为小于Q1-1.5 * IQR或大于Q3+1.5 * IQR的值。

以下是IQR方法的实现步骤：

Q1 = data['feature'].quantile(0.25)
Q3 = data['feature'].quantile(0.75)
IQR = Q3 - Q1

# 定义离群值阈值
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

# 确定离群值
outliers_iqr = data[(data['feature'] < lower_bound) | (data['feature'] > upper_bound)]['feature']

print("IQR离群值数量：", outliers_iqr.shape[0])
print("离群值：\n", outliers_iqr)

通过以上离群值检测方法，我们可以初步了解数据集中的异常情况，并为下一步的处理提供参考。

### 5.3 离群值处理

在确定了离群值后，我们需要对这些离群值进行处理，以确保它们不会对线性回归模型的准确性造成负面影响。

#### 5.3.1 删除离群值

一种方法是直接删除离群值，当离群值数量较少且不太可能反映真实情况时，这是一种较为简单的处理方法。

# 删除Z-Score方法检测到的离群值
data_cleaned = data.drop(outliers.index)

# 删除IQR方法检测到的离群值
data_cleaned_iqr = data.drop(outliers_iqr.index)

#### 5.3.2 替换离群值

对于某些情况下离群值无法删除的情况，可以考虑通过替换的方式处理，比如用中位数或均值来替代离群值。

# 用中位数替换Z-Score方法检测到的离群值
data['feature'].loc[z_scores > threshold] = data['feature'].median()

# 用均值替换IQR方法检测到的离群值
data['feature'].loc[data['feature'] < lower_bound] = data['feature'].mean()
data['feature'].loc[data['feature'] > upper_bound] = data['feature'].mean()

#### 5.3.3 离群值转换

另一种处理离群值的方式是对其进行转换，比如对数转换或截断转换，使其趋近于正常范围内的值。

# 对数转换
data['feature_log'] = np.log(data['feature'])

# 截断转换
data['feature_truncate'] = np.where(data['feature'] > upper_bound, upper_bound, np.where(data['feature'] < lower_bound, lower_bound, data['feature']))

通过上述离群值处理方法，我们可以更好地调整数据集，使其更适合进行线性回归建模。

### 5.4 线性回归建模

最后，我们进行线性回归建模，使用清理过的数据集进行模型训练和预测。

首先，我们导入线性回归模型并拟合数据：

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

X = data_cleaned[['feature']]
y = data_cleaned['target']

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 初始化线性回归模型
model = LinearRegression()

# 拟合模型
model.fit(X_train, y_train)

接着，我们可以进行模型评估，比如计算均方误差等指标：

# 预测
y_pred = model.predict(X_test)

# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print("均方误差：", mse)

通过以上步骤，我们完成了离群值检测、处理以及线性回归建模的整个流程。这样的案例分析有助于我们更深入地理解离群值对线性回归的影响以及如何应对这些影响。

# 6.1 高级离群值检测算法
在前面的章节中，我们已经介绍了一些常见的离群值检测方法，包括基于统计学方法、基于距离的方法以及基于密度的方法。在实际的数据处理中，有时候我们需要更高级的算法来应对复杂的场景。本节将介绍一些高级离群值检测算法，帮助我们更好地识别异常值。

#### 6.1.1 One-Class SVM
One-Class SVM（Support Vector Machine）是一种基于支持向量机的离群值检测算法。它的基本思想是通过构建一个超平面来将正常样本与离群样本分离开来，在高维空间中找到最优的分割超平面。相对于传统的 SVM，One-Class SVM 只关注一类样本（正常样本），并尝试找到一个最小的包围区域，这个区域内的样本被认为是正常的，而区域外的样本则被视为离群值。

在实际应用中，One-Class SVM 可以应用于数据集中离群值比较少、数据分布比较规则的情况下，能够很好地识别出潜在的异常值。

下面我们来看一个简单的示例，使用 Python 的 scikit-learn 库来实现 One-Class SVM 离群值检测算法：

# 导入必要的库
from sklearn import svm
import numpy as np

# 创建一些示例数据
X = np.array([[1, 2], [1, 3], [2, 2], [8, 8], [9, 8]])

# 定义 One-Class SVM 模型
clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.1)
clf.fit(X)

# 预测离群值
pred = clf.predict(X)
print(pred)

代码解释：
- 首先导入需要的库，并创建一个简单的二维数据集 X。
- 然后定义 One-Class SVM 模型，设定参数并训练模型。
- 最后预测数据集 X 中的离群值，并输出结果。

#### 6.1.2 Isolation Forest
Isolation Forest 是一种基于随机森林的离群值检测算法。它利用了树的分支深度来识别离群值，通过构建一棵随机树来对数据进行分割，离群值通常具有更短的路径长度。相比于其他算法，Isolation Forest 的计算效率更高，并且对大规模数据集有良好的适应性。

让我们通过一个实例来演示 Isolation Forest 的使用：

# 导入必要的库
from sklearn.ensemble import IsolationForest
import numpy as np

# 创建一些示例数据
X = np.array([[1, 2], [1, 3], [2, 2], [8, 8], [9, 8]])

# 定义 Isolation Forest 模型
clf = IsolationForest(contamination=0.1)
clf.fit(X)

# 预测离群值
pred = clf.predict(X)
print(pred)

这段代码展示了如何使用 scikit-learn 中的 Isolation Forest 模型对数据集 X 进行离群值检测，并输出预测结果。

以上就是关于高级离群值检测算法 One-Class SVM 和 Isolation Forest 的简单介绍和示例代码。在实际应用中，根据数据集的特点选择合适的离群值检测算法是非常重要的，通过不断尝试和实践，我们可以更好地理解和应用这些算法。