密度图在数据分析中的应用：从探索性分析到预测建模，全面掌握密度图的实用价值

# 1. 密度图简介及其在数据分析中的作用

密度图是一种可视化工具，用于描述数据分布的形状和趋势。它通过将数据点绘制为平滑的曲线来显示数据点的频率分布。密度图在数据分析中扮演着至关重要的角色，因为它可以帮助我们：

- **可视化数据分布：**密度图可以直观地显示数据的形状和中心趋势，帮助我们了解数据的分布情况。
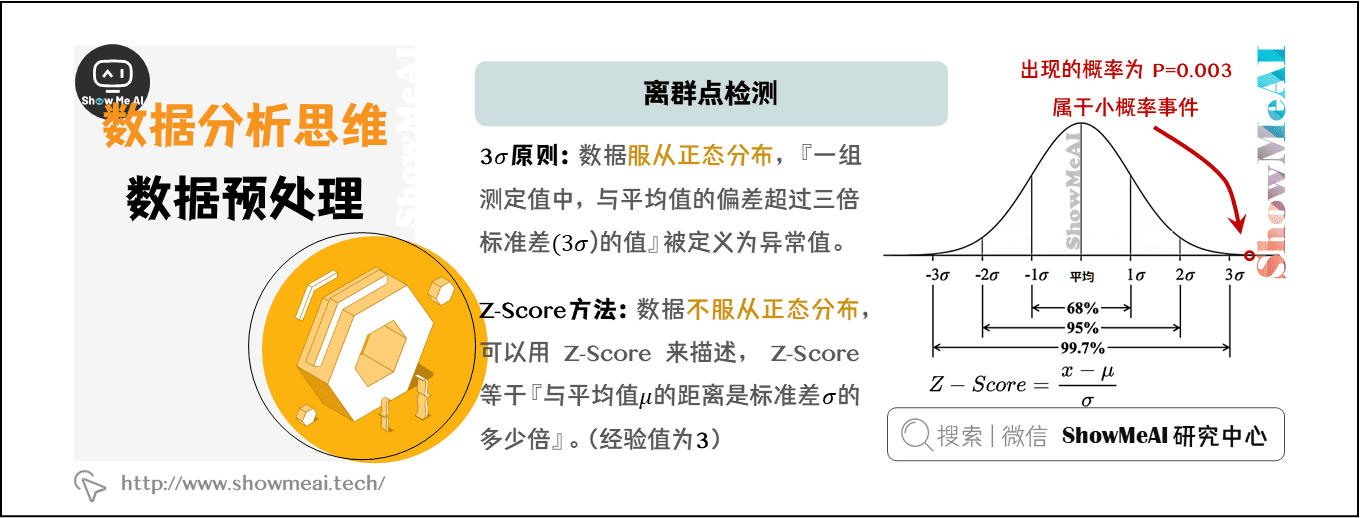
- **检测异常值：**密度图中的异常值会以孤立的峰值或低谷的形式出现，可以帮助我们识别数据中的异常点。
- **比较多变量数据：**密度图可以用于比较不同变量的数据分布，帮助我们了解变量之间的关系和差异。

# 2. 密度图的理论基础

### 2.1 概率密度函数和核密度估计

#### 概率密度函数

概率密度函数 (PDF) 描述了随机变量在特定值的概率分布。对于连续随机变量，PDF 表示为：

f(x) = dP(X = x) / dx

其中：

- `f(x)` 是随机变量 `X` 在 `x` 处的概率密度
- `P(X = x)` 是 `X` 等于 `x` 的概率

#### 核密度估计

核密度估计 (KDE) 是一种非参数方法，用于估计连续随机变量的 PDF。它通过使用一个称为核函数的平滑函数来对数据点进行加权。

核函数是一个非负对称函数，其积分等于 1。常用的核函数包括：

- 高斯核
- Epanechnikov 核
- 三角核

KDE 的公式为：

f(x) = (1 / n) * ∑[K((x - x_i) / h) / h]

其中：

- `n` 是数据点的数量
- `x_i` 是第 `i` 个数据点
- `h` 是带宽参数，控制核函数的平滑程度

### 2.2 密度图的绘制方法和参数选择

#### 绘制方法

密度图可以通过以下方法绘制：

- **直方图：** 将数据划分为离散的箱，并计算每个箱中的数据点数量。
- **核密度估计：** 使用 KDE 估计 PDF，然后绘制曲线。
- **多边形拟合：** 将数据点连接成多边形，以近似 PDF。

#### 参数选择

密度图的绘制需要选择以下参数：

- **带宽参数 (h)：** 控制核函数的平滑程度。较小的 `h` 值产生更平滑的密度图，但可能会隐藏细节。较大的 `h` 值产生更粗糙的密度图，但可能会显示更多细节。
- **核函数：** 选择核函数的类型会影响密度图的形状。高斯核产生平滑的曲线，而 Epanechnikov 核产生更尖锐的峰值。
- **分箱数 (直方图)：** 直方图中箱子的数量会影响密度图的分辨率。较多的箱子产生更精细的密度图，但可能会产生锯齿状的边缘。较少的箱子产生更粗糙的密度图，但边缘更平滑。

通过调整这些参数，可以优化密度图以显示数据的特定特征。

# 3.1 数据分布的可视化和异常值检测

密度图在探索性数据分析中，最直观的应用就是数据分布的可视化。通过绘制密度图，可以快速了解数据的分布情况，包括中心趋势、离散程度和形状等特征。例如，下图展示了不同分布的数据的密度图：

import numpy as np
import matplotlib.pyplot as plt

# 正态分布
data_normal = np.random.normal(0, 1, 1000)
plt.figure(figsize=(10, 5))
plt.hist(data_normal, density=True, bins=50, l