OpenCV图像变换性能优化：加速图像处理，提升效率，让图像变形更流畅

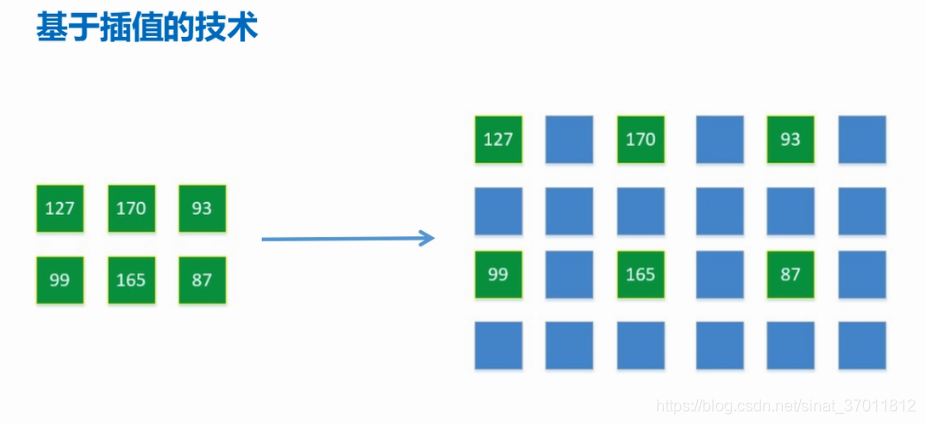
# 1. 图像变换概述**

图像变换是计算机视觉中一种重要的技术，它涉及对图像进行几何或像素值操作，以增强、分析或处理图像。图像变换可用于图像配准、图像增强、目标检测和图像压缩等广泛应用中。

图像变换可以分为两大类：空间域变换和频域变换。空间域变换直接对图像像素进行操作，而频域变换将图像转换为频域，然后在频域中进行操作。空间域变换包括平移、旋转和缩放等几何变换，而频域变换包括傅里叶变换和小波变换等。

# 2. 图像变换算法

图像变换算法是图像处理中的核心技术，它可以通过改变图像中的像素位置或像素值来实现图像的各种处理效果。图像变换算法主要分为两大类：空间域变换和频域变换。

### 2.1 空间域变换

空间域变换直接对图像中的像素进行操作，包括平移变换、旋转变换和缩放变换。

#### 2.1.1 平移变换

平移变换将图像中的所有像素沿水平或垂直方向移动一个指定的距离。平移变换的数学表达式为：

T(x, y) = (x + dx, y + dy)

其中，`(x, y)` 为原始像素坐标，`(dx, dy)` 为平移距离。

#### 2.1.2 旋转变换

旋转变换将图像中的所有像素围绕一个指定的中心点旋转一个指定的角度。旋转变换的数学表达式为：

R(x, y) = (x cos θ - y sin θ, x sin θ + y cos θ)

其中，`(x, y)` 为原始像素坐标，`θ` 为旋转角度。

#### 2.1.3 缩放变换

缩放变换将图像中的所有像素按比例放大或缩小。缩放变换的数学表达式为：

S(x, y) = (sx * x, sy * y)

其中，`(x, y)` 为原始像素坐标，`(sx, sy)` 为缩放比例。

### 2.2 频域变换

频域变换将图像从空间域转换为频域，在频域中对图像进行处理，然后将处理后的图像转换回空间域。频域变换主要包括傅里叶变换和小波变换。

#### 2.2.1 傅里叶变换

傅里叶变换将图像中的像素值分解为正弦波和余弦波的叠加，从而得到图像的频谱。傅里叶变换的数学表达式为：

F(u, v) = ∑∑ f(x, y) e^(-2πi(ux + vy))

其中，`(u, v)` 为频域坐标，`(x, y)` 为空间域坐标，`f(x, y)` 为原始图像像素值。

#### 2.2.2 小波变换

小波变换将图像中的像素值分解为小波函数的叠加，从而得到图像的时频表示。小波变换的数学表达式为：

W(s, t) = ∑∑ f(x, y) ψ(s, t, x, y)

其中，`(s, t)` 为时频坐标，`(x, y)` 为空间域坐标，`f(x, y)` 为原始图像像素值，`ψ(s, t, x, y)` 为小波函数。

# 3. 图像变换优化技术

图像变换在计算机视觉和图形处理中广泛应用，但随着图像尺寸和复杂度的不断增加，图像变换的计算成本也随之提高。为了提高图像变换的效率，需要采用优化技术来减少计算时间和资源消耗。本章将介绍两种常用的图像变换优化技术：并行化和算法优化。

### 3.1 并行化

并行化是一种通过同时使用多个处理单元来提高计算效率的技术。在图像变换中，并行化可以应用于多个方面，例如：

#### 3.1.1 多线程并行

多线程并行是指将图像变换任务分解成多个子任务，并由多个线程同时执行这些子任务。这种方