搜索算法与AI：Python智能化搜索升级指南

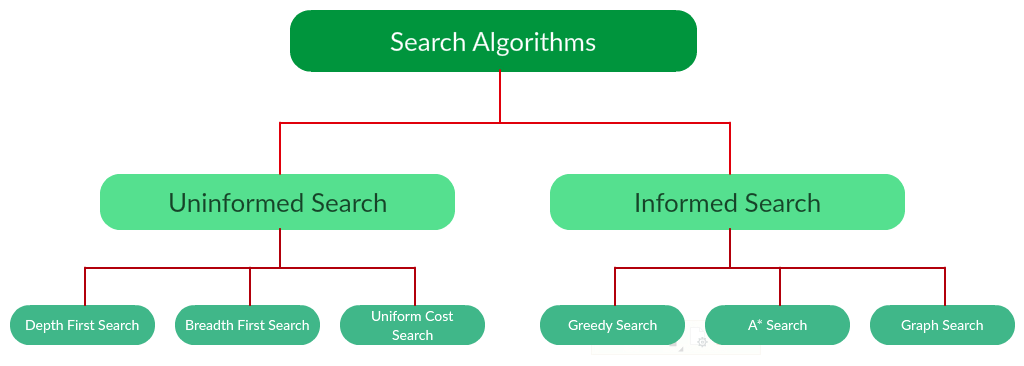
# 1. 搜索算法的基本概念与原理

搜索算法是计算机科学中用于查找数据项或路径的算法，广泛应用于各类计算机程序中。简单来说，搜索算法试图在各种可能的数据集中找到满足某些条件的项。要深入理解搜索算法，我们首先需要掌握几个基本概念：搜索空间、搜索策略和搜索效率。

搜索空间指的是算法进行搜索的可能解的集合，而搜索策略定义了搜索过程中解的选择方式。搜索效率，则是衡量搜索算法性能的重要指标，通常包括时间复杂度和空间复杂度两个方面。时间复杂度反映了算法完成任务所需的时间，而空间复杂度体现了算法在运行过程中对内存的需求。

理解搜索算法的原理，可以帮助我们更好地选择和设计适合特定问题的搜索策略。在后续章节中，我们将具体探讨不同类型的搜索算法以及它们在Python语言中的实现。

# 2. Python中的搜索算法实现

## 2.1 线性搜索与二分搜索

### 2.1.1 线性搜索的实现与应用

线性搜索是最基础的搜索算法之一，它通过顺序遍历数据结构中的所有元素来寻找特定目标值。尽管效率较低，但线性搜索在最坏情况下依然能找到目标元素，且适用于未排序或无法排序的数据集。

以下是Python实现线性搜索的简单示例代码：

def linear_search(data, target):
    for index, value in enumerate(data):
        if value == target:
            return index
    return -1

# 示例数据集
example_data = [5, 3, 7, 1, 9, 11]

# 查找特定值
target_value = 7
result = linear_search(example_data, target_value)

if result != -1:
    print(f"元素 {target_value} 在列表中的位置为 {result}")
else:
    print(f"列表中不存在元素 {target_value}")

在上述代码中，我们定义了`linear_search`函数来遍历数据集。此函数逐个检查元素，一旦找到与目标值匹配的元素，函数即返回该元素的索引。如果遍历完整个数据集仍未找到目标值，函数返回`-1`，表示未找到目标。

线性搜索在实际应用中具有普遍性，尤其是对于小型数据集或数据无明显规律时非常适用。在Python中，线性搜索通常是学习搜索算法的起点，也是理解更复杂搜索算法的基础。

### 2.1.2 二分搜索的原理及在Python中的实现

二分搜索算法，又称为折半搜索，是一种高效的搜索算法，它要求待搜索的数据结构必须是有序的。通过将数据集分成两半，以此来排除一半的数据，从而迅速缩小搜索范围。

下面是一个在Python中实现二分搜索的代码示例：

def binary_search(data, target):
    left, right = 0, len(data) - 1
    while left <= right:
        mid = (left + right) // 2
        if data[mid] == target:
            return mid
        elif data[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

# 已排序的数据集
sorted_data = [1, 3, 5, 7, 9, 11, 13]
target_value = 7

# 执行二分搜索
result = binary_search(sorted_data, target_value)

if result != -1:
    print(f"元素 {target_value} 在列表中的位置为 {result}")
else:
    print(f"列表中不存在元素 {target_value}")

在此代码段中，`binary_search`函数通过不断将搜索范围减半来查找目标值。函数初始化两个指针，分别指向数据集的开始和结束位置，通过循环不断比较中间值与目标值，以此来缩小搜索范围。

二分搜索算法的时间复杂度为O(log n)，这使得它在处理大型有序数据集时非常高效。不过，维护数据的有序性可能需要额外的时间复杂度，因此在某些情况下，二分搜索的总体效率可能会受到排序成本的影响。

## 2.2 深度优先搜索与广度优先搜索

### 2.2.1 深度优先搜索的理论基础与代码实例

深度优先搜索（DFS）是一种用于遍历或搜索树或图的算法。其核心思想是从一个节点出发，尽可能深地搜索，直到达到最深点，然后回溯。DFS常用于解决迷宫问题、路径寻找以及网络爬虫等。

下面是深度优先搜索在Python中的一个简单实现示例：

def dfs(graph, node, visited=None):
    if visited is None:
        visited = set()
    visited.add(node)
    print(node)
    for neighbor in graph[node]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)
    return visited

# 示例图结构
graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}

# 执行深度优先搜索
dfs(graph, 'A')

在这个例子中，`dfs`函数递归地遍历图结构。每个节点被访问后即加入到已访问集合`visited`中，避免重复访问。然后，函数继续递归地对每个未访问的邻居节点调用自身。

### 2.2.2 广度优先搜索的逻辑及Python实现方法

广度优先搜索（BFS）是另一种图遍历算法，它从一个节点开始，先访问所有邻近节点，然后依次对这些邻近节点的邻近节点进行访问，直到所有的节点都被访问过。这种算法适用于求解最短路径问题，以及查找两个节点之间是否存在路径等。

下面是一个使用Python实现的广度优先搜索示例代码：

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        vertex = queue.popleft()
        if vertex not in visited:
            visited.add(vertex)
            print(vertex)
            queue.extend([n for n in graph[vertex] if n not in visited])
    return visited

# 示例图结构
graph = {
    'A': ['B', 'C'],
    'B': ['A', 'D', 'E'],
    'C': ['A', 'F'],
    'D': ['B'],
    'E': ['B', 'F'],
    'F': ['C', 'E']
}

# 执行广度优先搜索
bfs(graph, 'A')

在上述代码中，我们使用`deque`数据结构来存储待访问的节点，这样可以保证先进先出的顺序。`bfs`函数首先将起始节点加入队列，然后通过循环来遍历图，每次从队列中取出一个节点，访问它并将其未访问的邻居加入队列中。

## 2.3 启发式搜索与A*算法

### 2.3.1 启发式搜索的基本原理

启发式搜索是一种基于特定规则（称为启发式函数）的搜索策略，旨在快速找到问题的解。它通过评估每个步骤的成本来选择最优路径，常用于路径规划、游戏AI和机器学习等领域。与传统的盲目搜索方法相比，启发式搜索减少了不必要的搜索，提高了搜索效率。

### 2.3.2 A*算法的详解与Python代码实现

A*算法是启发式搜索中最有影响力的一个算法，它结合了最好优先搜索和最短路径搜索的优点。算法评估每个节点的“f”值，该值是通过将从起始点到当前节点的实际代价（g）与从当前节点到目标的估计代价（h）相加得到的。

下面是一个在Python中实现的A*算法的示例代码：

import heapq

class Node:
    def __init__(self, position, parent=None):
        self.position = position
        self.parent = parent
        self.g = 0  # Cost from start to current node
        self.h = 0  # Heuristic cost from current node to goal
        self.f = 0  # Total cost

    def __eq__(self, other):
        return self.position == other.position

    def __lt__(self, other):
        return self.f < other.f

def a_star_search(graph, start, goal):
    open_list = []
    closed_list = set()
    start_node = Node(start)
    goal_node = Node(goal)
    heapq.heappush(open_list, start_node)

    while open_list:
        current_node = heapq.heappop(open_list)
        closed_list.add(curre