热分析有限元方法：工程师必备的温度控制技巧


# 摘要
本文全面概述了热分析有限元方法的基本概念、理论基础及其在现代工程中的应用。通过对热力学第一定律、热传导方程、有限元分析数学基础的深入探讨，为热分析提供了坚实的理论支撑。文章还详细介绍了有限元软件在热分析中的应用，包括基本操作、材料属性处理、温度场模拟等方面，并探讨了温度控制技巧、热应力分析以及多物理场耦合等高级技术。通过工业和电子设备热分析的案例研究，本文强调了理论与实践相结合的重要性，并对热分析方法的未来发展趋势和研究前沿提出了展望。

# 关键字
热分析；有限元方法；热力学；数值模拟；温度控制；多物理场耦合

参考资源链接：[《有限元法：理论、格式与求解方法（第2版）》- 巴特（Bathe）](https://wenku.csdn.net/doc/2u7pcni3f5?spm=1055.2635.3001.10343)
# 1. 热分析有限元方法概述

热分析有限元方法是一种强大的数值分析技术，它能够在复杂几何形状和多变材料属性的系统中模拟温度分布和热流。本章将对热分析有限元方法进行基础性介绍，为后续章节奠定理论和实践基础。

## 1.1 热分析的重要性
在工程设计和产品开发过程中，温度的影响无处不在。热分析可以预测在特定操作条件下的温度分布，从而对材料的选择、热应力管理和热疲劳寿命进行评估。这对于确保产品长期可靠运行至关重要。

## 1.2 有限元方法在热分析中的作用
有限元方法（FEM）在热分析中允许工程师以数值方式求解复杂的偏微分方程，尤其是热传导方程。FEM通过将连续体划分为小的、有限大小的元素，简化了问题，并允许模拟包括不规则形状在内的各种几何结构。

## 1.3 热分析有限元方法的步骤
进行热分析通常包括以下步骤：
- 建立数学模型：定义问题的控制方程，通常是热传导方程。
- 网格划分：将模型划分为有限元网格。
- 应用边界条件和初始条件。
- 求解线性或非线性方程组，得到温度分布。
- 结果分析与优化：根据结果调整设计以改善热性能。

接下来的章节将详细探讨热力学基础、有限元理论、软件应用、实践技巧和案例研究，帮助读者深入理解并运用热分析有限元方法解决实际问题。

# 2. 热力学基础与有限元理论

### 2.1 热力学第一定律与能量守恒

热力学第一定律，也被称为能量守恒定律，是物理学中描述能量转换和守恒的基础原理。在热分析领域，这一原理至关重要，因为它为研究热能与其他形式能量之间的相互转化提供了理论基础。

#### 2.1.1 热力学系统与环境

在热力学中，系统是指我们关注的物理实体，而环境则是指系统之外的部分。一个热力学系统的热能变化等于系统与环境之间交换的热量与系统对外做的功的代数和。用数学公式表达即：

\[ \Delta U = Q - W \]

其中，ΔU表示系统内能的改变，Q表示系统从环境中吸收的热量，W表示系统对外做的功。在有限元分析中，这一原理有助于我们建立材料或组件内部热能分布与外部环境之间的关系。

#### 2.1.2 能量转换与守恒定律

能量转换指的是热能、机械能、电能等不同形式的能量之间的转换。能量守恒定律指出，在一个封闭系统内，能量不能被创造或销毁，只能从一种形式转换成另一种形式。因此，在一个热力学过程中，能量的转换必须遵循守恒原则。在热分析有限元模型中，这意味着热能的产生、传递和耗散必须满足这一守恒定律。

### 2.2 热传导方程与边界条件

热传导方程描述了热能在介质内部的传递规律，边界条件则是描述系统边界上的热交换特性。在热分析有限元模型中，它们共同构成了分析问题的数学基础。

#### 2.2.1 热传导方程的推导

热传导方程，也称为傅里叶定律，可以表示为：

\[ \frac{\partial T}{\partial t} = \alpha \nabla^2 T + \frac{q}{k} \]

其中，T表示温度，t表示时间，α表示材料的热扩散率，∇^2表示拉普拉斯算子，q表示单位体积的热源项，k表示热导率。热传导方程是从能量守恒和傅里叶定律推导出来的，它表征了温度随时间和空间的变化。

#### 2.2.2 不同边界条件的应用

边界条件在热传导方程中起着至关重要的作用，它们描述了物体表面与外部环境的热交换。常见的边界条件包括：

1. 第一类边界条件（Dirichlet边界条件）：固定温度，T=T0。
2. 第二类边界条件（Neumann边界条件）：固定热流，q=-k∇T·n。
3. 第三类边界条件（Robin边界条件）：对流热交换，q=h(T-T∞)。

在有限元软件中，根据实际情况选择合适的边界条件是准确模拟热传导过程的关键。例如，在模拟电子设备的散热时，可能需要考虑对流边界条件，其中h是热传递系数，T∞是环境温度。

### 2.3 有限元分析的数学基础

有限元分析是一种利用数学近似方法对实际问题进行数值解的计算技术。其数学基础包括变分原理和离散化过程。

#### 2.3.1 变分原理与泛函

变分原理为泛函最小化问题提供了解决方案。在热分析中，我们关心的是能量泛函，比如热能，它通常与温度分布有关。泛函是一个函数的函数，具体到热分析中，可以表示为系统的总热能。

泛函最小化可表示为求解如下变分问题：

\[ \delta \Pi = 0 \]

这里的Π是总热能泛函，而δΠ是泛函的变分。解决这一问题可以确定系统的温度分布，从而得到热传导方程的解。

#### 2.3.2 离散化过程与元素类型

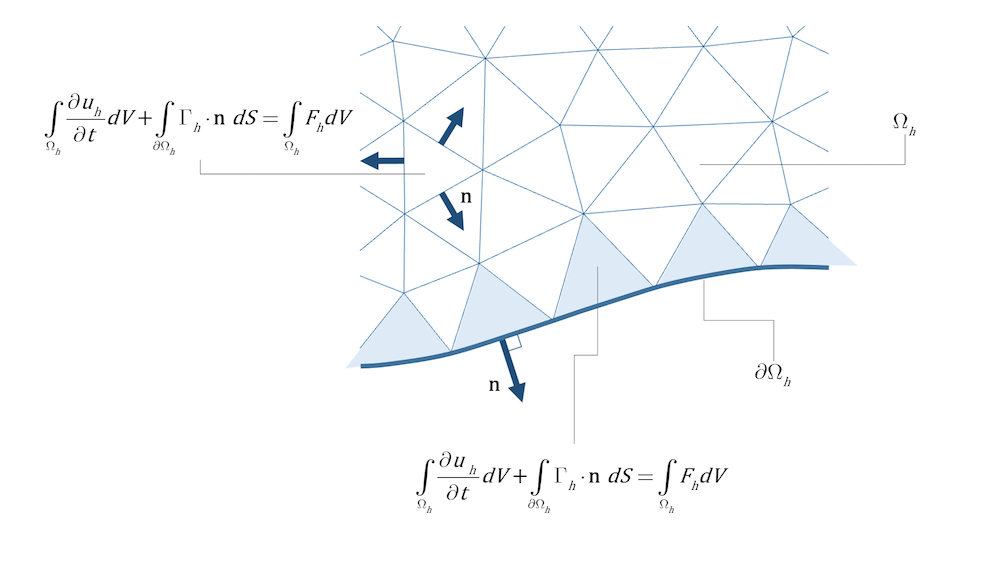
在有限元分析中，连续的物理域被划分为有限个单元（或元素），每个单元之间通过节点相互连接。离散化过程是有限元分析的核心步骤，它通过近似函数将连续域映射到离散域。根据问题的不同，选择的单元类型也不同，常见的包括：

- 一维线性单元
- 二维三角形和矩形单元
- 三维四面体和六面体单元

离散化后，通过单元的节点温度插值来逼近整个域内的温度分布。每个单元的温度场可以用形函数和节点温度表示，通过求解线性方程组，可以计算出整个物理域的温度分布。

通过本章节的介绍，读者应能够理解热力学基础与有限元理论在热分析领域的核心作用，以及如何将理论应用于有限元软件的热分析模型构建中。在后续章节中，我们将深入了解有限元软件的具体操作和应用，以及如何利用这些工具进行热分析和优化。

# 3. 有限元软件在热分析中的应用

## 3.1 有限元软件的基本操作

### 3.1.1 软件界面与建模步骤

在有限元分析过程中，选择合适的软件是至关重要的一步。当前市场上存在多种成熟的有限元分析软件，如ANSYS, ABAQUS, COMSOL Multiphysics等，它们各有特色，能高效完成从建模到分析的全过程。以ANSYS为例，其软件界面通常包括以下几个主要模块：

- **前处理模块**：用于建立模型、定义材料属性、网格划分、边界条件和载荷施加等。
- **求解器模块**：执行数学计算，对模型进行求解。
- **后处理模块**：用于查看、分析和解释计算结果。

具体操作流程如下：

1. **启动软件并新建项目**：启动ANSYS软件后，通过File菜单选择New Project创建新的分析项目。
2. **定义材料属性**：在材料库中选择或定义所需的材料属性，包括导热系数、密度、比热容等。
3. **几何建模**：使用DesignModeler或SpaceClaim等工具创建或导入几何模型。
4. **网格划分**：通过Mesh模块对模型进行网格划分，以准备后续的分析。
5. **施加载荷和边界条件**：根据实际工况设置载荷（如温度场、热流密度）和边界条件（如对流换热、固定温度等）。
6. **求解**：设置求解器参数，进行求解计算。
7. **后处理**：通过结果查看器分析计算得到的温度分布、热流线等数据。

### 3.1.2 网格划分与单元选择

网格划分是有限元分析中将连续体离散化的过程，以模拟各种复杂的几何和材料特性。网格类型和单元的选择直接影响计算的精度和效率。以下是网格划分和单元选择的基本步骤：

1. **选择单元类型**：根据分析类型选择合适的单元类型。对于热分析，通常选用三维热实体单元，如ANSYS中的SOLID70或COMSOL中的Heat Transfer Module。
2. **设定网格尺寸**：根据模型的复杂程度和细节调整网格尺寸，确保足够的计算精度。
3. **自适应网格细化**：利用软件提供的自适应网格细化功能，根据计算误差自动调整网格密度。
4. **检查网格质量**：确保网格形状合理，没有过度扭曲的单元，以减少求解误差。

在网格划分时，可采用的策略包括