模拟信号处理中的RC电路：信号衰减与整形技术详解


# 摘要
本文详细探讨了RC电路在信号处理中的基础原理、信号衰减机制、信号整形应用以及高级信号处理技术。通过分析RC电路的基本数学模型和时间常数，阐述了信号在RC电路中的衰减原理，以及低通、高通、带通和带阻滤波器的工作机制。文章还深入讨论了RC电路在信号整形功能中的设计原则和实际应用，包括整流电路设计与实现、平滑滤波和信号稳定性。此外，本文介绍了非线性RC电路的应用、数据采集系统中的RC电路实现，以及RC电路集成与模块化设计的优势。最后，文章提供了RC电路设计和实验优化的技巧，包括常见问题解决、仿真技术和实验设计的实践技巧，为电路设计人员和实验者提供了宝贵的参考。

# 关键字
RC电路；信号处理；信号衰减；信号整形；滤波器；电路设计优化

参考资源链接：[理解RC电路：时间常数、响应与应用详解](https://wenku.csdn.net/doc/1dhhy054us?spm=1055.2635.3001.10343)
# 1. RC电路基础与信号处理原理

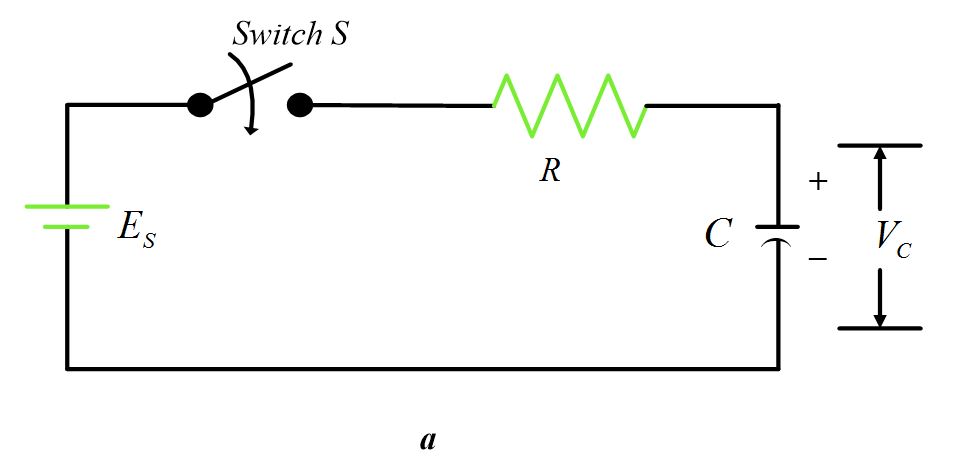
在讨论RC电路如何处理信号之前，我们首先需要了解RC电路的构成和基本原理。RC电路由电阻器（Resistor）和电容器（Capacitor）组成，是一个最基本的模拟电子电路。理解RC电路如何响应不同频率的信号变化，是掌握其在信号处理中作用的关键。

## 1.1 RC电路的信号响应基础

RC电路的信号响应涉及到电阻和电容对电流和电压变化的响应特性。电阻阻碍电流流动，而电容则储存电荷并延缓电压变化。当输入一个交变信号时，RC电路会根据电阻和电容的相对大小，影响信号的相位和幅度。信号频率越低，电容充电时间越短，信号衰减越小；频率越高，充电时间越长，信号衰减越大。

## 1.2 信号处理中的RC电路应用

在信号处理中，RC电路常被用作简单的滤波器，如低通、高通或带通滤波器，它们能够根据信号频率的不同，滤除不需要的信号成分或通过所需的频率范围。此外，RC电路还能用于信号的积分和微分运算，以及信号波形的整形等。

## 1.3 RC电路中的时间常数τ

RC电路中的时间常数τ（tau），定义为电阻值R乘以电容值C，即τ=RC。时间常数决定了电路对信号响应的速度。例如，在一个低通滤波器中，τ决定了信号通过电路时，高频信号成分衰减的速度。理解时间常数对于设计RC电路以达到特定的信号处理效果至关重要。

# 2. RC电路中的信号衰减机制

在电子工程和信号处理领域，RC电路扮演着不可或缺的角色。本章将深入探讨RC电路中的信号衰减机制，理解这一现象的数学模型、理论分析以及在实验室环境中的应用。

## 2.1 电阻-电容电路的数学模型

### 2.1.1 RC电路的基本方程

RC电路是电学领域中最基本的电路之一，由一个电阻（R）和一个电容（C）组成，它们通过电容器两端的电压和流过电阻的电流来表征电路的动态行为。RC电路的基本方程是一个一阶线性微分方程：

\[ V(t) + RC \frac{dV(t)}{dt} = V_{source}(t) \]

这里，\( V(t) \)是电容器两端的电压随时间\( t \)的变化，\( V_{source}(t) \)是输入电压源，\( RC \)就是我们熟知的时间常数\( \tau \)。通过解析这个微分方程，我们可以得到RC电路的响应特性，了解电容器是如何随着时间充电或放电的。

### 2.1.2 时间常数τ与电路响应

时间常数\( \tau = RC \)是RC电路中一个非常重要的参数，它定义了电路达到其最终状态（例如充电或放电到最终电压值）所需的时间。在理想情况下，时间常数可以告诉我们电容器电压达到其最终电压值的63.2%所需要的时间。

时间常数\( \tau \)可以用来计算电容器充电或放电的半衰期（电压降至其初始值的一半所需时间）：

\[ \tau = t_{1/2} \cdot \ln(2) \]

这表明，每经过一个时间常数，电容器的电压变化量都将是一个固定的比例。随着时间的推移，电压的变化将越来越慢，直到趋于稳定。

## 2.2 信号衰减的理论分析

### 2.2.1 低通滤波器的工作原理

RC电路可以作为低通滤波器，允许低频信号通过而衰减高频信号。电路中的电阻和电容共同作用，使得电路对频率的响应呈现特定的滤波特性。在低频下，电容器的阻抗较高，电路行为近似于开路；在高频下，电容器的阻抗较低，电路行为近似于短路。

数学上，RC电路的传递函数为：

\[ H(f) = \frac{1}{1 + j2\pi fRC} \]

其中\( f \)是信号的频率，\( H(f) \)是滤波器的频率响应函数，\( j \)是虚数单位。频率响应函数表明，频率越高，信号的幅度衰减越大。

### 2.2.2 高通滤波器的工作原理

同理，RC电路也可以实现高通滤波功能，但其滤波特性与低通滤波器相反。在高频下，电容器的阻抗较高，信号能够通过；而在低频下，电容器的阻抗较低，信号被衰减。

高通滤波器的传递函数形式与低通类似，但频率响应函数的变量是频率的倒数：

\[ H(f) = \frac{j2\pi fRC}{1 + j2\pi fRC} \]

### 2.2.3 带通和带阻滤波器的衰减特性

RC电路同样可以组合成带通和带阻滤波器，分别允许特定频率范围内的信号通过以及衰减特定频率范围内的信号。带通滤波器的构建通常需要两个RC电路串联，并各自形成一个低通和高通滤波器。带阻滤波器则是通过两个RC电路并联实现。

## 2.3 实验室中的信号衰减技术

### 2.3.1 实验设备与测量方法

在实验室中进行RC电路的信号衰减实验，需要的基本设备包括：信号发生器、示波