量子算法性能评估

# 1. 量子算法性能评估概述

量子算法作为量子计算领域的核心内容，其性能评估是推动该领域发展的重要环节。评估过程涉及对量子算法理论基础的理解、分类与原理的分析，以及实施性能测试的实验方法。本章主要介绍量子算法性能评估的基本概念，以及其在量子计算中的重要性。

量子计算的特性使得其算法在某些问题上能够超越传统计算模型的性能，因此，如何有效评估量子算法的性能，成为量子计算研究和应用中的一个关键挑战。在此基础上，本章还将对性能评估的必要性和可能面临的挑战进行简要概述，为读者搭建一个全面了解量子算法性能评估的基础框架。

- 量子算法性能评估的必要性
- 评估过程涉及的关键概念
- 对量子计算发展的影响

# 2. 量子计算的理论基础

## 2.1 量子比特与量子态
### 2.1.1 量子比特的特性

量子比特（qubit）是量子计算中的基本信息单位，它与传统的比特有着本质的不同。传统的比特只能处于0或1的状态，而量子比特可以通过量子叠加原理同时处于0和1的状态。这种叠加状态用数学表示就是两个状态的线性组合，可以写成 |ψ⟩ = α|0⟩ + β|1⟩，其中|ψ⟩是量子比特的状态，α和β是复数概率幅，它们的模方分别表示测量得到0或1的概率。

### 2.1.2 量子态的表示方法

量子态的表示方法中最常见的是狄拉克符号，例如|ψ⟩表示一个量子态。量子态的演化可以用薛定谔方程来描述，即iħ(d/dt)|ψ(t)⟩ = H|ψ(t)⟩，其中i是虚数单位，ħ是约化普朗克常数，H是哈密顿算符。量子态的测量通常采用算符来描述，测量结果是算符本征态的概率分布。具体来说，测量一个量子态|ψ⟩，得到本征态|φ⟩的概率是|⟨φ|ψ⟩|²。

## 2.2 量子门与量子电路
### 2.2.1 量子门的种类与功能

量子门是作用于一个或多个量子比特上的可逆操作，它在量子计算中的角色相当于传统计算中的逻辑门。量子门的种类繁多，包括单量子比特门如Pauli-X、Y、Z门，Hadamard门和相位门；以及双量子比特门如CNOT门和CZ门。这些量子门可以单独使用，也可以组合起来执行复杂的操作。量子门的一个关键特性是它们必须是幺正的，意味着它们必须保持量子态的叠加性质并且保持概率幅的总和为1。

### 2.2.2 量子电路的构建原理

量子电路是由量子门序列组成的，用于在量子计算机上执行算法。构建量子电路时需要遵循逻辑门的顺序排列，其中量子比特的传输线对应传统电路中的导线。在设计量子电路时，还需要考虑到量子比特间的纠缠关系和门操作的同步性。量子电路可以通过抽象的数学描述和量子门组合的图示来表达，最终目的是构造出能够解决特定问题的量子算法。

## 2.3 量子纠缠与量子并行性
### 2.3.1 量子纠缠的概念与应用

量子纠缠是量子力学中一个非常特别的现象，当两个量子比特发生纠缠时，它们的状态不能被独立描述，而是需要作为一个整体来处理。即使两个量子比特被分隔很远的距离，对其中一个量子比特的测量也会立即影响到另一个量子比特的状态。这一特性在量子通信和量子计算中都有重要应用。例如，在量子密钥分发中，量子纠缠用于生成和分发密钥；在量子计算中，它可以用于实现量子并行性，提高计算速度。

### 2.3.2 量子并行计算的优势与限制

量子并行性是指在量子计算中可以同时处理多个计算路径的能力。由于量子叠加，单个量子比特可以代表多种可能性，而多个量子比特的叠加状态可以代表指数级的可能组合，这是传统计算机无法实现的。量子并行性允许量子计算机在执行某些特定算法时比经典计算机快得多，例如Shor算法分解大整数和Grover算法进行数据库搜索。然而，量子并行性并非万能，存在某些问题并不具备量子加速潜力，且实际的量子并行计算仍然面临诸多技术挑战，例如量子比特的相干时间、错误率和可扩展性等问题。

# 3. 量子算法的分类与原理

## 3.1 量子搜索算法

### 3.1.1 Grover算法的原理与实现

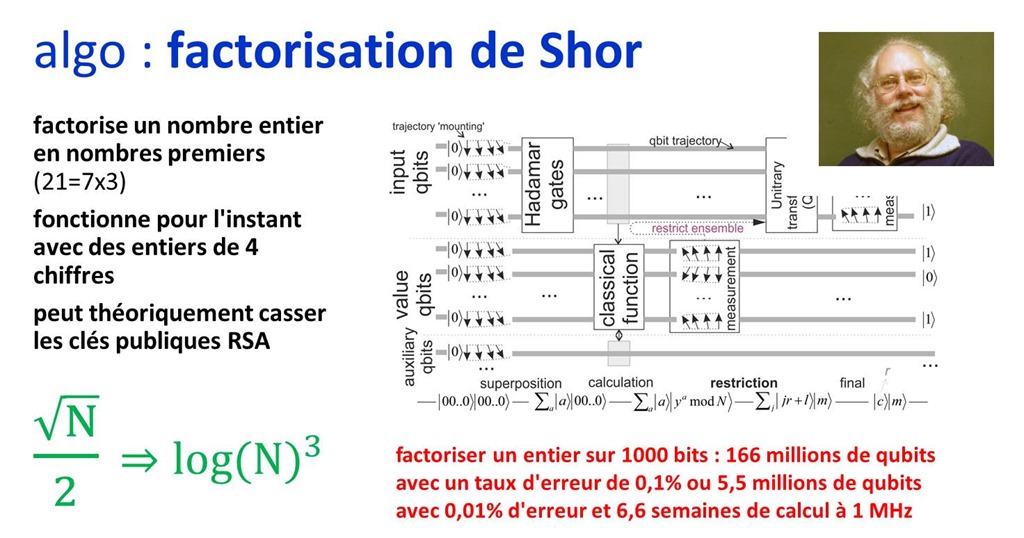
Grover算法是一种量子搜索算法，由Lov Grover于1996年提出，用于解决无序数据库的搜索问题。该算法能显著地减少搜索所需的操作步骤，其时间复杂度为O(√N)，相对于经典算法的O(N)有了巨大的提升。

在实现上，Grover算法使用了量子叠加态和量子干涉原理来提升目标状态的概率振幅。算法过程中，初始将所有量子比特置于等幅叠加态，然后通过一系列特定的量子操作——特别是量子反演操作（Grover算子）来增强目标状态的振幅。

以下是Grover算法的基本步骤：

1. 初始化：将n个量子比特初始化到等幅叠加态。
2. 应用Oracle：Oracle函数标记出满足搜索条件的目标状态。
3. 应用振幅放大操作：通过量子反演算子放大目标状态的振幅。
4. 反复迭代：重复步骤2和步骤3，直至量子态具有足够大的概率坍缩到目标状态。

为了更具体地理解Grover算法的实现，以下是一个使用Qiskit（IBM的量子计算软件开发包）的Python示例代码：

from qiskit import Aer, execute
from qiskit.circuit.library import GroverOperator
from qiskit.visualization import plot_histogram

# 创建一个量子电路
oracle = ... # 定义Oracle函数，用于标记目标状态
grover = GroverOperator(oracle)
qc = QuantumCircuit(grover.num_qubits)

# 初始化量子电路到等幅叠加态
qc.h(range(grover.num_qubits))

# 应用Grover算子
qc.append(grover, range(grover.num_qubits))

# 测量量子比特并输出结果
qc.measure_all()

在上述代码中，我们需要定义一个Oracle函数来标记目标状态，然后创建Grover算子，应用到初始的量子叠加态上，并在最后进行测量以得到搜索结果。代码中并没有详尽地展示如何定义Oracle函数，因为这取决于具体搜索问题的定义。

### 3.1.2 搜索问题的量子加速

量子搜索算法的核心优势在于利用了量子叠加和量子干涉的性质。量子叠加使得量子计算机能够同时处理大量的状态，而量子干涉则允许算法通过特定的操作放大目标状态的概率，从而实现搜索的加速。

对于搜索问题来说，Grover算法的加速体现在其平方根的复杂度上。考虑一个包含N个元素的无序数据库，经典算法需要检查每一项，平均需要N/2次操作。Grover算法通过量子干涉，只需要大约√N次操作就可以找到目标项，这在处理大规模数据时尤为显著。

这种加速并不是针对特定问题的，而是基于量子力学原理对广泛搜索问题的一般性改进。量子搜索算法在密码学、数据库检索等领域都有潜在的应用价值。

在实际应用中，量子搜索算法需要考虑的不仅仅是理论的加速。量子噪声、错误以及量子比特数量等因素都会影响算法的实际效率和实用性。随着量子硬件技术的不断进步，我们可以期待在不久的将来，量子搜索算法将在更多领域显示出其强大的计算能力。

## 3.2 量子模拟与量子化学

### 3.2.1 量子模拟的基本方法

量子模拟是指使用量子计算机来模拟另一个量子系统的行为。在经典计算中，模拟量子系统是非常困难的，因为需要大量的计算资源来跟踪指数级增长的状态。而量子计算机天然适合执行这样的模拟，因为它们可以自然地表示量子态，并且能够以量子力学的方式相互作用。

量子模拟的基本方法包括：

1. **直接模拟**：直接将量子系统映射到量子计算机的量子比特上，并通过量子门操作来模拟系统内部的动态演化。这种方法的优点是直观且易于理解，但其局限在于能够模拟的量子系统大小受限于量子计算机当前的技术水平。
2. **辅助量子模拟**：这种方法利用辅助量子比特来处理复杂的交互。它包括将系统的某一部分编码到辅助比特上，然后再与主系统的量子比特进行相互作用，从而实现对整个系统的模拟。这种技术在处理较为复杂的系统时显得尤为有效。

3. **时间演化模拟**：通过连续的量子门操作来模拟量子态随时间的演化。这通常涉及使用特定的量子电路来近似时间演化算符。

量子模拟的一个重要应用是在量子化学领域，用以计算分子和材料的电子结构。这包括了解分子的最低能级（基态）和激发态，这对于新材料的设计和化学反应的研究至关重要。

### 3.2.2 量子化学