揭秘算术运算在计算机科学中的15个应用：从基础到前沿

# 1. 算术运算的基础知识

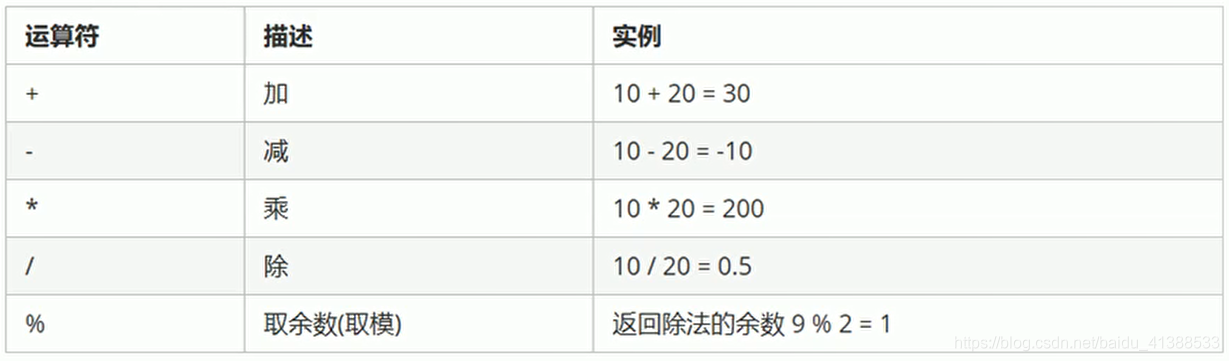
算术运算，又称基本运算，是计算机科学中最重要的基础知识之一。它包括加、减、乘、除、取模等基本操作，是构建更复杂算法和数据结构的基础。

在计算机中，算术运算通常使用二进制进行，即以 0 和 1 两个数字表示所有数字。二进制运算的速度比十进制运算快得多，并且更适合计算机的电子电路。

算术运算在计算机科学中有着广泛的应用，从简单的数值计算到复杂的数据处理。例如，在密码学中，素数生成和判定是公钥加密算法的基础；在图论中，最短路径算法和最大流最小割定理用于解决网络优化问题；在人工智能中，神经网络的训练和优化依赖于复杂的算术运算。

# 2. 算术运算在计算机科学中的应用

算术运算在计算机科学的各个领域中扮演着至关重要的角色，为各种算法、数据结构和应用提供了基础。本章节将探讨算术运算在以下领域的应用：

### 2.1 数论和密码学

#### 2.1.1 素数生成和判定

素数在密码学中具有重要意义，因为它们用于生成密钥和确保数据的安全。素数生成和判定算法是数论中的基本问题。

**素数生成算法**

* **费马素性检验：**使用费马小定理确定一个数字是否为素数。
* **米勒-拉宾素性检验：**使用随机化算法来确定一个数字是否为素数。

**素数判定算法**

* **埃拉托斯特尼筛法：**通过筛除非素数来生成素数列表。
* **AKS素性检验：**使用代数方法确定一个数字是否为素数。

#### 2.1.2 公钥加密算法

公钥加密算法依赖于素数的性质来确保数据的安全。

**RSA算法**

* **密钥生成：**选择两个大素数p和q，计算n=pq。生成公钥(e,n)和私钥(d,n)。
* **加密：**明文M加密为C=M^e mod n。
* **解密：**密文C解密为M=C^d mod n。

### 2.2 图论和算法

#### 2.2.1 最短路径算法

最短路径算法用于在图中找到两个节点之间的最短路径。

**Dijkstra算法**

* **参数：**图G，源节点s。
* **逻辑：**
* 初始化所有节点的距离为无穷大，s的距离为0。
* 重复以下步骤，直到所有节点都被访问过：
* 找到当前未访问的节点中距离最小的节点u。
* 对于u的所有相邻节点v，更新v的距离为min(v.distance, u.distance + u->v.weight)。
* 返回每个节点的距离。

#### 2.2.2 最大流最小割定理

最大流最小割定理在图论中用于解决网络流问题。

**最大流最小割定理**

* **定义：**对于一个网络流，最大流等于最小割。
* **最大流算法：**
* **福特-福克森算法：**使用增广路径算法找到最大流。
* **最小割算法：**
* **Edmonds-Karp算法：**使用最大流算法找到最小割。

### 2.3 数据结构和算法

#### 2.3.1 数组和链表的实现

数组和链表是计算机科学中常用的数据结构。

**数组**

* **参数：**元素类型T，数组长度n。
* **逻辑：**
* 使用连续内存空间存储元素。
* 通过索引访问元素。
* **优点：**访问速度快，空间利用率高。
* **缺点：**插入和删除操作效率低。

**链表**

* **参数：**元素类型T。
* **逻辑：**
* 使用节点存储元素，每个节点包含元素值和指向下一个节点的指针。
* 通过遍历指针访问元素。
* **优点：**插入和删除操作效率高。
* **缺点：**访问速度慢，空间利用率低。

#### 2.3.2 排序算法和查找算法

排序算法和查找算法用于对数据进行组织和检索。

**排序算法**

* **冒泡排序：**通过逐个比较相邻元素来排序。
* **快速排序：**使用分治策略来排序。
* **归并排序：**使用分治策略来排序，时间复杂度为O(n log n)。

**查找算法**

* **二分查找：**对于已排序的数组，使用二分法查找元素。
* **哈希表：**使用哈希函数将元素映射到存储位置，以快速查找。
* **B树：**一种自平衡搜索树，用于高效查找和插入操作。

# 3.1 神经网络和机器学习

**3.1.1 神经网络的训练和优化**

神经网络是一种受生物神经元启发的机器学习模型，它由相互连接的层组成，每层包含多个神经元。神经元接收输入，执行非线性变换，并产生输出。通过训练神经网络，可以学习复杂的模式和关系。

神经网络的训练过程涉及调整连接权重和偏差，以最小化损失函数。损失函数衡量网络预测与实际标签之间的差异。常用的优化算法包括梯度下降、动量和自适应矩估计（Adam）。

**代码块 1：神经网络训练**

import tensorflow as tf

# 创建神经网络模型
model = tf.keras.Sequential([
  tf.keras.layers.Dense(128, activation='relu', input_shape=(784,)),
  tf.keras.layers.Dense(10, activation='softmax')
])

# 编译模型
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

# 训练模型
model.fit(x_train, y_train, epochs=10)

**逻辑分析：**

* `model.compile()`：编译模型，指定优化器、损失函数和指标。
* `model.fit()`：训练模型，使用给定的训练数据和指定的训练周期（epochs）。

**3.1.2 机器学习算法的评估**

机器学习算法的评估对于衡量其性能至关重要。常用的评估指标包括准确率、召回率、F1 分数和混淆矩阵。

**代码块 2：机器学习算法评估**

from sklearn.metrics import accuracy_score, recall_score, f1_score, confusion_matrix

# 预测测试数据
y_pred = model.predict(x_test)

# 计算评估指标
accuracy = accuracy_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)
confusion = confusion_matrix(y_test, y_pred)

**逻辑分析：**

* `model.predict()`：使用训练好的模型对测试数据进行预测。
* `sklearn.metrics`：使用 Scikit-Learn 库计算评估指标。

### 3.2 自然语言处理

**3.2.1 文本相似度计算**

文本相似度计算是自然语言处理中的一项基本任务，它用于衡量两段文本之间的相似程度。常用的文本相似度度量包括余弦相似度、欧几里得距离和莱文斯坦距离。

**代码块 3：文本相似度计算**

import numpy as np
from sklearn.metrics.pairwise import cosine_similarity

# 计算余弦相似度
text1 = "This is a sample text."
text2 = "This is another sample text."
vector1 = tf.keras.preprocessing.text.Tokenizer().texts_to_matrix([text1])
vector2 = tf.keras.preprocessing.text.Tokenizer().texts_to_matrix([text2])
similarity = cosine_similarity(vector1, vector2)

**逻辑分析：**

* `tf.keras.preprocessing.text.Tokenizer()`：将文本转换为词向量。
* `cosine_similarity()`：计算余弦相似度，范围从 0（不相似）到 1（完全相似）。

**3.2.2 情感分析**

情感分析是一种自然语言处理技术，用于识别和提取文本中的情感。常用的情感分析方法包括词袋模型、词嵌入和卷积神经网络。

**代码块 4：情感分析**

import tensorflow as tf

# 创建情感分析模型
model = tf.keras.Sequential([
  tf.keras.layers.Embedding(10000, 128),
  tf.keras.layers.Conv1D(128, 5, activation='relu'),
  tf.keras.layers.GlobalMaxPooling1D(),
  tf.keras.layers.Dense(1, activation='sigmoid')
])

# 编译模型
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

# 训练模型
model.fit(x_train, y_train, epochs=10)

**逻辑分析：**

* `tf.keras.layers.Embedding()`：将单词转换为词嵌入。
* `tf.keras.layers.Conv1D()`：使用卷积层提取文本特征。
* `tf.keras.layers.GlobalMaxPooling1D()`：获取序列中最重要的特征。
* `tf.keras.layers.Dense()`：使用全连接层进行分类。

### 3.3 计算机视觉

**3.3.1 图像处理和增强**

图像处理和增强是计算机视觉中常用的技术，用于改善图像质量和提取有用的信息。常见的图像处理操作包括缩放、旋转、裁剪和颜色调整。

**代码块 5：图像处理**

import cv2

# 缩放图像
image = cv2.imread("image.jpg")
scaled_image = cv2.resize(image, (256, 256))

# 旋转图像
rotated_image = cv2.rotate(image, cv2.ROTATE_90_CLOCKWISE)

# 裁剪图像
cropped_image = image[100:200, 100:200]

# 调整颜色
adjusted_image = cv2.cvtColor(image, cv2.COLOR_BGR2HSV)

**逻辑分析：**

* `cv2.imread()`：读取图像。
* `cv2.resize()`：缩放图像。
* `cv2.rotate()`：旋转图像。
* `cv2.cvtColor()`：转换图像颜色空间。

**3.3.2 目标检测和识别**

目标检测和识别是计算机视觉中的高级任务，用于定位和识别图像中的对象。常用的目标检测算法包括 YOLO、Faster R-CNN 和 SSD。

**代码块 6：目标检测**

import cv2
import numpy as np

# 加载 YOLO 模型
net = cv2.dnn.readNet("yolov3.weights", "yolov3.cfg")

# 预处理图像
image = cv2.imread("image.jpg")
blob = cv2.dnn.blobFromImage(image, 1 / 255.0, (416, 416), (0, 0, 0), swapRB=True, crop=False)

# 运行模型
net.setInput(blob)
detections = net.forward()

# 解析检测结果
for detection in detections:
    confidence = detection[5]
    if confidence > 0.5:
        x1, y1, x2, y2 = detection[0:4] * np.array([image.shape[1], image.shape[0], image.shape[1], image.shape[0]])
        cv2.rectangle(image, (x1, y1), (x2, y2), (0, 255, 0), 2)

**逻辑分析：**

* `cv2.dnn.readNet()`：加载 YOLO 模型。
* `cv2.dnn.blobFromImage()`：预处理图像。
* `net.setInput()`：将预处理后的图像输入模型。
* `net.forward()`：运行模型并获得检测结果。
* `cv2.rectangle()`：在图像上绘制检测到的目标。

# 4. 算术运算在高性能计算中的应用

算术运算在高性能计算中发挥着至关重要的作用，它为解决复杂问题和处理海量数据提供了强大的计算能力。本章将探讨算术运算在并行编程、数值模拟和科学计算、大数据分析和处理等高性能计算领域的应用。

### 4.1 并行编程和分布式计算

并行编程和分布式计算是高性能计算中常用的技术，它们通过将计算任务分解为多个并行执行的子任务，从而提高计算效率。算术运算在并行编程和分布式计算中扮演着关键角色，它用于执行子任务之间的通信和数据交换。

**4.1.1 多线程和多进程编程**

多线程和多进程编程是并行编程的两种常见方法。多线程在同一进程中创建多个线程，这些线程共享相同的内存空间。多进程则创建多个独立的进程，每个进程都有自己的内存空间。算术运算在多线程和多进程编程中用于执行线程或进程之间的同步和通信。

import threading

# 创建一个共享变量
shared_variable = 0

# 创建一个线程函数
def increment_shared_variable():
    global shared_variable
    shared_variable += 1

# 创建两个线程
thread1 = threading.Thread(target=increment_shared_variable)
thread2 = threading.Thread(target=increment_shared_variable)

# 启动线程
thread1.start()
thread2.start()

# 等待线程结束
thread1.join()
thread2.join()

# 打印共享变量的值
print(shared_variable)  # 输出：2

在上面的代码中，`shared_variable`是一个共享变量，两个线程同时对它进行加法操作。`threading.Lock()`用于同步线程对共享变量的访问，确保线程安全。

**4.1.2 分布式计算框架**

分布式计算框架是一种软件平台，它允许在多台计算机上并行执行计算任务。算术运算在分布式计算框架中用于处理任务之间的通信和数据交换。

例如，Apache Spark是一个流行的分布式计算框架，它使用算术运算来执行数据转换、聚合和排序等操作。

### 4.2 数值模拟和科学计算

数值模拟和科学计算涉及到对复杂物理现象进行建模和求解。算术运算在数值模拟和科学计算中用于执行大量的浮点运算，这些运算对于求解偏微分方程、模拟流体动力学等问题至关重要。

**4.2.1 有限元分析**

有限元分析是一种数值模拟技术，它将复杂结构分解为更小的单元，并使用算术运算来求解单元之间的相互作用。算术运算在有限元分析中用于计算应力、应变和位移等物理量。

**4.2.2 流体力学模拟**

流体力学模拟涉及到对流体流动进行建模和求解。算术运算在流体力学模拟中用于执行复杂的浮点运算，这些运算对于求解纳维-斯托克斯方程等偏微分方程至关重要。

### 4.3 大数据分析和处理

大数据分析和处理涉及到处理和分析海量数据集。算术运算在大数据分析和处理中用于执行数据预处理、特征提取、数据挖掘和知识发现等任务。

**4.3.1 数据预处理和特征提取**

数据预处理和特征提取是数据分析中的重要步骤，它们涉及到对原始数据进行清洗、转换和提取有价值的特征。算术运算在大数据预处理和特征提取中用于执行数据标准化、归一化和降维等操作。

**4.3.2 数据挖掘和知识发现**

数据挖掘和知识发现是通过分析大数据集来发现隐藏模式和趋势的过程。算术运算在大数据挖掘和知识发现中用于执行聚类、分类和回归等机器学习算法。

import pandas as pd
from sklearn.cluster import KMeans

# 加载数据
data = pd.read_csv('data.csv')

# 标准化数据
data = (data - data.mean()) / data.std()

# 创建 KMeans 聚类模型
model = KMeans(n_clusters=3)

# 训练模型
model.fit(data)

# 预测数据
labels = model.predict(data)

# 打印聚类结果
print(labels)

在上面的代码中，`KMeans`算法使用算术运算来计算数据点之间的距离和聚类中心。`pd.read_csv()`和`pd.DataFrame.std()`函数用于数据加载和标准化。

# 5. 算术运算的前沿应用

### 5.1 量子计算

#### 5.1.1 量子算法和量子计算机

量子计算是一种利用量子力学原理进行计算的新型计算范式。与传统计算机不同，量子计算机利用量子比特（qubit）作为基本计算单元，具有叠加和纠缠的特性。这些特性使得量子计算机在解决某些特定问题上具有传统计算机无法比拟的优势。

量子算法是专门针对量子计算机设计的算法。与传统算法相比，量子算法通常具有以下特点：

- **并行性：** 量子比特可以同时处于多个状态，这使得量子算法可以并行执行多个操作。
- **指数加速：** 对于某些特定问题，量子算法的时间复杂度可以达到指数级加速。

目前，量子计算机还处于早期发展阶段，但已经取得了显著的进展。谷歌、IBM 等科技巨头都在积极研发量子计算机，并取得了一系列突破。

#### 5.1.2 量子密码学

量子密码学是利用量子力学原理实现安全通信的技术。与传统密码学不同，量子密码学利用量子密钥分发（QKD）技术，可以生成绝对安全的密钥。

QKD 的原理是利用量子比特的叠加和纠缠特性。通过发送纠缠的量子比特，通信双方可以建立一个安全密钥，即使窃听者截获了量子比特，也无法破解密钥。

量子密码学具有以下优势：

- **绝对安全：** 基于量子力学原理，量子密码学密钥无法被破解。
- **长距离传输：** 量子密钥可以在长距离上传输，不受距离限制。

目前，量子密码学技术已经开始应用于金融、政府等领域，为这些领域提供了更加安全的通信保障。