MATLAB求反函数的深度探索：揭秘其内部机制和实现

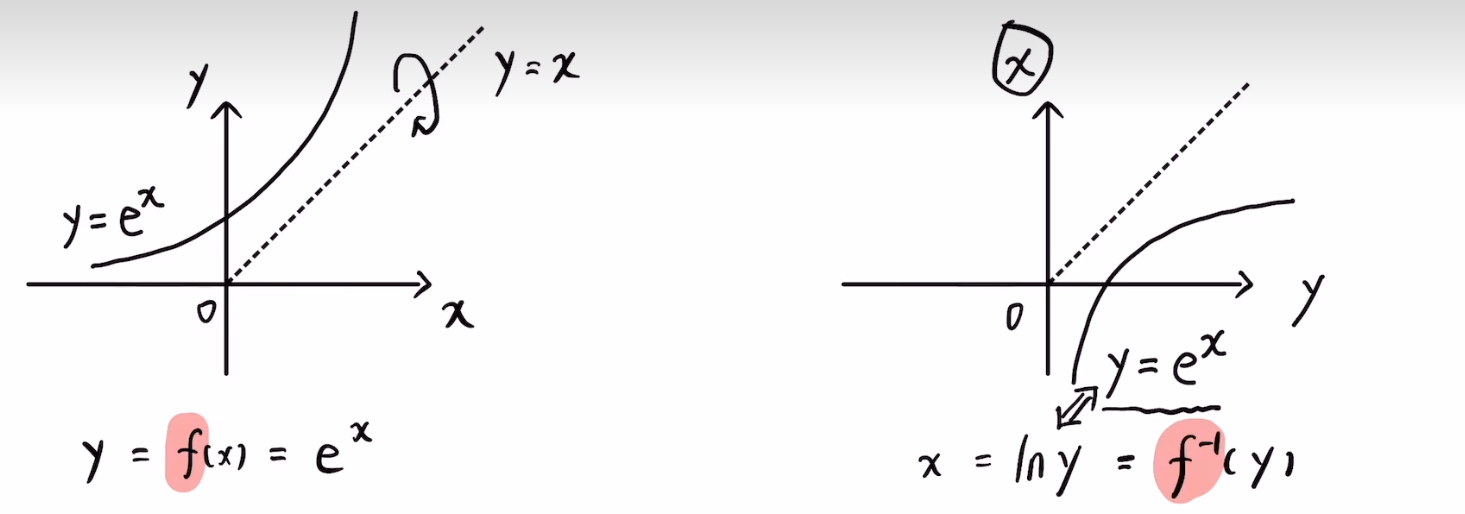
# 1. MATLAB求反函数简介

反函数是数学中一个重要的概念，它表示一个函数的逆运算。在MATLAB中，求解反函数是一个常见的任务，它在数据拟合、图像处理和优化等领域有着广泛的应用。

本指南将介绍MATLAB中求反函数的理论基础、实践方法和进阶应用。我们将探讨反函数的概念和性质，以及求解反函数的不同方法。此外，我们还将展示如何使用MATLAB求解反函数，并讨论其在实际问题中的应用。

# 2. 求反函数的理论基础

### 2.1 反函数的概念和性质

#### 2.1.1 反函数的定义

反函数是函数的一种特殊类型，它将原函数的因变量作为自变量，而将原函数的自变量作为因变量。换句话说，如果 f(x) 是一个函数，那么它的反函数 f^-1(x) 是满足 f(f^-1(x)) = x 且 f^-1(f(x)) = x 的函数。

#### 2.1.2 反函数的性质和条件

反函数具有以下性质：

- **单调性：**反函数是单调递增或单调递减的。
- **对称性：**反函数的图像关于 y = x 直线对称。
- **范围和值域：**反函数的范围是原函数的值域，反函数的值域是原函数的范围。

反函数存在的条件是：

- **单射性：**原函数必须是单射的，即对于不同的自变量，函数值不同。
- **连续性：**原函数必须在反函数的定义域内连续。

### 2.2 求反函数的方法

#### 2.2.1 代数法

代数法是求反函数最基本的方法。对于一个显式函数 f(x)，可以通过以下步骤求得其反函数：

1. 交换 x 和 y。
2. 求解 y 关于 x 的方程。
3. 将 y 替换为 f^-1(x)。

例如，求函数 f(x) = 2x + 1 的反函数：

y = 2x + 1
x = 2y + 1
y = (x - 1) / 2
f^-1(x) = (x - 1) / 2

#### 2.2.2 图形法

图形法是一种直观的求反函数的方法。对于一个函数 f(x)，其反函数 f^-1(x) 的图像可以如下获得：

1. 绘制 f(x) 的图像。
2. 关于 y = x 直线对称 f(x) 的图像。
3. 对称后的图像即为 f^-1(x) 的图像。

#### 2.2.3 数值法

数值法是一种近似求解反函数的方法。对于一个隐式函数 f(x, y) = 0，可以使用牛顿迭代法或其他数值方法来近似求解 y 关于 x 的方程，从而得到反函数 f^-1(x)。

# 3. MATLAB求反函数的实践

### 3.1 使用MATLAB求反函数

#### 3.1.1 反函数求解命令

MATLAB中提供了`inv`命令用于求矩阵的反函数。其语法格式为：

Y = inv(X)

其中：

* `X`：待求反的矩阵
* `Y`：求得的反函数矩阵

#### 3.1.2 反函数求解示例

考虑以下矩阵：

A = [2 1; -1 3]

使用`inv`命令求其反函数：

B = inv(A)

输出结果为：

B =
    0.6    -0.2
    0.2     0.4

可以验证，`B * A`和`A * B`都等于单位矩阵，表明`B`是矩阵`A`的反函数。

### 3.2 MATLAB求反函数的应用

#### 3.2.1 数据拟合

反函数在数据拟合中有着广泛的应用。例如，考虑以下数据集：

x = [1, 2, 3, 4, 5];
y = [2, 4, 6, 8,