社交媒体数据分析：时间序列方法的探索之旅


参考资源链接：[王燕编著《应用时间序列分析》习题答案详解](https://wenku.csdn.net/doc/somtbpckqw?spm=1055.2635.3001.10343)
# 1. 社交媒体数据分析概述

社交媒体平台已经成为人们日常生活的一部分，它们不仅仅是用于交流和分享信息的工具，也成为了企业获取市场反馈、洞察用户行为和进行品牌营销的重要渠道。社交媒体数据分析是利用数据挖掘、统计分析和机器学习等技术，对社交媒体上的用户生成内容、互动行为和网络关系等数据进行深入分析的过程。通过对社交媒体数据的分析，我们可以揭示用户偏好、预测市场趋势、优化营销策略以及进行情感分析等。

社交媒体数据分析不仅限于获取简单的用户统计信息，还涉及从原始数据中提取深层次的洞见，比如通过自然语言处理技术来理解用户的评论情感，或者通过社交网络分析来挖掘关键影响者和信息传播路径。随着数据量的不断增加和分析技术的不断进步，社交媒体数据分析正在成为连接数据科学和商业决策的重要桥梁。

# 2. 时间序列分析的基础理论

时间序列分析是现代数据分析中一项重要的技术，尤其在金融、经济、社会科学和工程学等领域广泛应用。了解时间序列分析的基础理论是深入研究其应用和实践操作的前提。本章将深入探讨时间序列数据的特点和类型、统计特性分析，以及预测模型理论。

## 2.1 时间序列数据的特点和类型

### 2.1.1 时间序列的基本概念

时间序列是按照时间顺序排列的一系列数据点，每一个数据点都对应于特定的时间点或时间段。时间序列分析的目的是理解过去的数据并预测未来的趋势。时间序列分析广泛应用于股票价格预测、天气预测、销售趋势分析等领域。

在处理时间序列数据时，我们需要注意以下几个关键点：

- **时间点间隔**：数据点间隔可以是固定的（比如每小时、每天、每月）或者不规则的（比如交易发生的时间）。
- **时间跨度**：时间序列可以覆盖很短的时期，如几小时内的交易数据，也可以覆盖长达数十年的年际数据。
- **数据粒度**：时间序列数据的粒度决定了数据点的详细程度，比如日均气温与每分钟记录一次的气温。

### 2.1.2 时间序列的分类与特性

时间序列可以被分类为以下几种主要类型：

- **平稳时间序列**：序列的统计特性不随时间的推移而变化，例如均值、方差和协方差等。
- **非平稳时间序列**：序列的统计特性随时间的变化而变化，这类时间序列需要经过特定的处理才能变为平稳序列，才能使用某些预测模型。

时间序列的特性通常包括：

- **趋势**：长期运动方向，反映出数据的上升或下降。
- **季节性**：在固定周期内重复出现的模式。
- **周期性**：比季节性更长周期的重复模式，不一定有固定周期。
- **随机性**：不可预测的随机成分，通常来自于外界未被考虑的冲击。

## 2.2 时间序列的统计特性分析

### 2.2.1 常用的统计量和分布特征

对时间序列进行初步的统计分析是理解数据的基础。一些重要的统计量包括：

- **均值**：时间序列数据的平均水平。
- **方差和标准差**：数据的离散程度。
- **偏度**：描述数据分布的对称性。
- **峰度**：描述数据分布的尖峭程度。

此外，时间序列数据的分布特性也需要关注，比如正态分布、对数正态分布等。

### 2.2.2 趋势、季节性和周期性分析

- **趋势分析**：检测并建模时间序列的长期变化方向。
- **季节性分析**：识别和量化时间序列中的季节性成分。
- **周期性分析**：找出时间序列中的周期性波动，这些波动通常与商业周期、经济周期或自然周期有关。

## 2.3 时间序列的预测模型理论

### 2.3.1 移动平均模型

移动平均模型是一种简单的时间序列预测模型，通过计算时间序列数据中连续值的平均数来预测未来的值。它主要用来平滑数据，减弱随机波动的影响。移动平均模型分为简单移动平均（SMA）和加权移动平均（WMA）。

一个简单移动平均模型的计算公式如下：

def simple_moving_average(time_series, window_size):
    """
    计算简单移动平均值
    :param time_series: 时间序列数据列表
    :param window_size: 窗口大小
    :return: 移动平均列表
    """
    moving_averages = []
    for i in range(len(time_series) - window_size + 1):
        this_window = time_series[i : (i + window_size)]
        window_average = sum(this_window) / window_size
        moving_averages.append(window_average)
    return moving_averages

### 2.3.2 自回归模型及其变种

自回归（AR）模型是时间序列分析中另一个常用模型，该模型假设时间序列的当前值与前几个时间点的值有关。AR模型的数学表达形式如下：

# AR模型示例
import numpy as np

def ar_model(time_series, p):
    """
    自回归模型实现
    :param time_series: 时间序列数据列表
    :param p: 自回归项的阶数
    :return: 预测值
    """
    # 建立预测模型
    predictions = []
    for i in range(p, len(time_series)):
        y = time_series[i]
        ar系数 = np.polyfit(time_series[i-p:i], y, 1)[0]
        yhat = ar系数 * time_series[i-p]
        predictions.append(yhat)
    return predictions

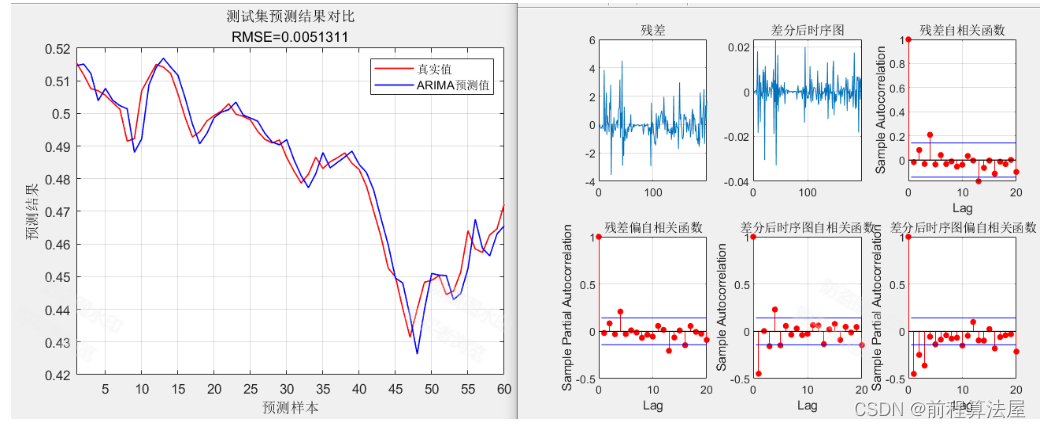
### 2.3.3 ARIMA模型及其组件

ARIMA模型是自回归移动平均模型（ARMA）与差分的结合体。它能够同时捕捉时间序列的自回归、移动平均和非平稳特性。ARIMA模型的构建包括三个部分：AR部分、差分部分I（Integrated）和MA部分。

构建ARIMA模型需要以下步骤：

1. **识别模型阶数**：确定ARIMA(p,d,q)中的p、d、q三个参数。
2. **模型参数估计**：使用历史数据对模型参数进行估计。
3. **模型检验**：检验残差是否为白噪声序列，确保模型拟合良好。
4. **预测**：使用拟合的模型进行未来时间点的预测。

代码示例：

from statsmodels.tsa.arima.model import ARIMA

def arima_model(time_series, p, d, q):
    """
    ARIMA模型预测函数
    :param time_series: 时间序列数据列表
    :param p: 自回归项的阶数
    :param d: 差分次数
    :param q: 移动平均项的阶数
    :return: 预测结果
    """
    model = ARIMA(time_series, order=(p, d, q))
    fitted_model = model.fit()
    forecast = fitted_model.forecast(steps=5)  # 预测未来5个数据点
    return forecast

通过本章节的介绍，我们不仅概述了时间序列分析的基础理论，还通过示例代码，进一步展示了如何应用这些理论进行实际的数据分析。这些知识为下一章的时间序列分析实践操作打下了坚实的基础。

# 3. 时间序列分析的实践操作

在现代数据分析领域，时间序列分析是一种非常强大的工具，能够揭示数据随时间变化的规律性。本章节将重点介绍时间序列数据的实际操作流程，包括数据预处理、模型建立与评估，以及通过具体案例来展示时间序列分析在社交媒体数据中的应用。

## 3.1 时间序列数据的预处理

### 3.1.1 数据清洗与整合

在进行时间序列分析之前，需要对原始数据进行清洗和整合。数据清洗包括剔除重复记录、处理缺失值、过滤异常值等。整合则是将多个数据源合并为一个连贯的时间序列。

在实践中，一个常见的预处理步骤是使用Python的Pandas库，该库提供了丰富的时间序列处理功能。

import pandas as pd

# 假设有一个名为social_media_data.csv的文件，包含社交媒体的帖子数据
df = pd.read_csv('social_media_data.csv', index_col='timestamp', parse_dates=True)

# 检查并处理缺失值
df = df.dropna()

# 过滤出特定条件的记录，例如仅保留包含特定话题的帖子
filtered_df = df[df['content'].str.contains('特定话题')]

# 输出处理后的数据
print(filtered_df.head())

通过上述步骤，我们得到了一个清洗和整合后的数据集，为后续的分析奠定了基础。

### 3.1.2 数据的平稳性检验与转换

时间序列的平稳性是指统计特性不随时间变化。在进行预测之前，需要对数据进行平稳性检验，如ADF检验（Augmented Dickey-Fuller Test）。

from statsmodels.tsa.stattools import adfuller

# 进行ADF检验
adf_test = adfuller(filtered_df['指标列'])
print('ADF Statistic: %f' % adf_test[0])
print('p-value: %f' % adf_test[1])

如果检验出数据不平稳，可以使用差分、对数转换或Box-Cox转换等方法进行平稳化处理。

## 3.2 时间序列预测模型的建立与评估

### 3.2.1 模型的选择与训练

在确定数据平稳后，可以根据数据特征选择合适的模型进行训练。常见的模型包括ARIMA、SARIMA、Holt-Winters等。

from statsmodels.tsa.arima.model import