单片机控制柜PID控制原理与应用：精确定位和控制的权威指南

# 1. 单片机PID控制原理**

**1.1 PID控制的基本概念**

PID控制（比例-积分-微分控制）是一种经典的反馈控制算法，广泛应用于各种工业自动化系统中。其基本原理是通过测量被控对象的输出值与期望值之间的偏差，并根据偏差的大小和变化率，计算出适当的控制量，以减小偏差并使输出值接近期望值。

**1.2 PID控制器的结构和组成**

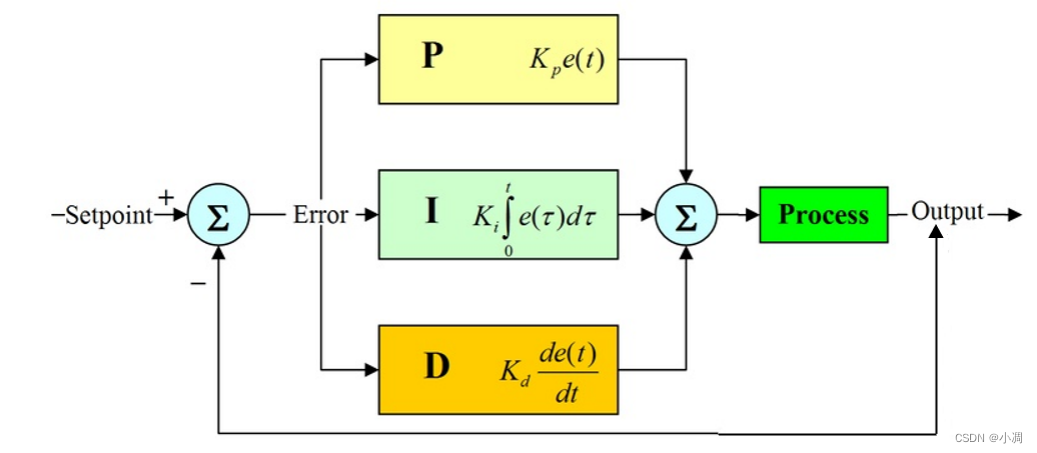
PID控制器由三个基本模块组成：比例模块（P）、积分模块（I）和微分模块（D）。每个模块的作用如下：

* **比例模块（P）：**根据偏差的大小产生一个与偏差成正比的控制量。
* **积分模块（I）：**根据偏差的积分产生一个与偏差积分成正比的控制量。
* **微分模块（D）：**根据偏差的变化率产生一个与偏差变化率成正比的控制量。

# 2. PID控制算法

### 2.1 PID算法的数学模型

PID算法是一个反馈控制算法，其数学模型由以下三个部分组成：

#### 2.1.1 比例控制（P）

比例控制项与控制误差成正比，即：

P = Kp * e(t)

其中：

* `P` 为比例控制输出
* `Kp` 为比例增益
* `e(t)` 为控制误差，即目标值与实际值之差

比例控制可以快速响应误差，但容易产生稳态误差。

#### 2.1.2 积分控制（I）

积分控制项与误差的积分成正比，即：

I = Ki * ∫e(t)dt

其中：

* `I` 为积分控制输出
* `Ki` 为积分增益
* `∫e(t)dt` 为误差的积分

积分控制可以消除稳态误差，但响应速度较慢。

#### 2.1.3 微分控制（D）

微分控制项与误差的导数成正比，即：

D = Kd * de(t)/dt

其中：

* `D` 为微分控制输出
* `Kd` 为微分增益
* `de(t)/dt` 为误差的导数

微分控制可以提高系统的稳定性和响应速度，但容易产生噪声放大。

### 2.2 PID算法的调参方法

PID算法的调参至关重要，常用的调参方法有：

#### 2.2.1 Ziegler-Nichols方法

Ziegler-Nichols方法是一种基于系统阶跃响应的调参方法，其步骤如下：

1. 将PID算法的积分和微分增益设为0，仅使用比例控制。
2. 逐渐增加比例增益，直到系统出现持续振荡。
3. 记录此时比例增益的临界值`Kp,c`和振荡周期`T,c`。
4. 根据`Kp,c`和`T,c`计算PID算法的增益：

Kp = 0.6 * Kp,c
Ki = 2 * Kp / T,c
Kd = Kp * T,c / 8

#### 2.2.2 渐近法

渐近法是一种基于系统响应的迭代调参方法，其步骤如下：

1. 先设置一个较小的比例增益，然后逐渐增加，直到系统响应接近理想。
2. 再设置一个较小的积分增益，然后逐渐增加，直到系统响应消除稳态误差。
3. 最后设置一个较小的微分增益，然后逐渐增加，直到系统响应稳定且无超调。

# 3.1 单片机PID控制系统的硬件架构

#### 3.1.1 单片机选型

单片机是单片机PID控制系统的核心，其性能直接影响系统的控制精度和响应速