【C语言递归排序深度剖析】：递归排序的巧妙运用

# 1. C语言递归排序概述

在计算机科学领域，排序算法是基础且重要的算法之一。它们广泛应用于数据处理、搜索优化、以及各种复杂的系统设计中。C语言作为一种高效、灵活的编程语言，常常用于实现各种排序算法，尤其是递归排序算法。

递归排序算法是一种利用递归思想来处理排序问题的方法，它包括快速排序、归并排序和堆排序等。这些算法通过递归地将大问题分解为小问题，并在小问题解决后合并结果，从而达到排序的目的。

在本章中，我们将首先对递归排序进行一个简单的概述，为读者建立起对递归排序的基础认识。这包括理解递归排序算法的工作原理，以及它在C语言中实现的特殊之处。在后续章节中，我们将进一步深入探讨递归排序的理论基础，实战演练以及高级话题，最终通过项目案例分析，深入理解递归排序在现实世界的应用。

# 2. 递归排序的理论基础

## 2.1 递归的数学原理
递归是计算机科学中一种强大的思想，它通过函数调用自身来解决问题。理解递归的数学原理，有助于我们深入掌握递归排序算法的工作机制。

### 2.1.1 递归定义及其特性
递归是一种编程技巧，也是一种解决问题的方法。它将问题分解为更小的子问题，而这些子问题的解决方法与原问题相同。

void function(int n) {
    if (n <= 1) return;
    function(n - 1); // 递归调用
    // 其他操作...
}

递归函数通常包含两个主要部分：基本情况（base case）和递归步骤（recursive step）。基本情况是递归结束的条件，而递归步骤则是函数调用自身的部分。

### 2.1.2 递归与数学归纳法
递归和数学归纳法有相似之处。归纳法通过证明基本情况为真，然后假设一般情况为真，来证明其归纳步骤也为真。递归中，基本情况作为递归终止的条件，而递归步骤则是依据较小规模的问题逐步求解。

// 使用递归解决斐波那契数列问题
int fibonacci(int n) {
    if (n == 0) return 0;
    if (n == 1) return 1;
    return fibonacci(n - 1) + fibonacci(n - 2); // 递归调用
}

## 2.2 排序算法的基本概念
在讨论递归排序算法之前，我们需要理解排序算法的基本概念和评价标准。

### 2.2.1 排序算法的分类和评价标准
排序算法可以根据是否使用比较操作、是否稳定、是否原地排序等标准进行分类。

- **比较排序**与**非比较排序**：比较排序算法在排序过程中需要进行元素之间的比较，而非比较排序算法则不需要。
- **稳定排序**：在排序过程中，相同值的元素保留原有顺序的排序方法称为稳定排序。
- **原地排序**：在排序过程中，不需要额外分配大量存储空间的排序方法。

排序算法的效率通常通过时间复杂度和空间复杂度来评价。时间复杂度描述了算法运行时间随输入规模增长的变化趋势，而空间复杂度描述了算法在运行过程中临时占用存储空间的大小。

### 2.2.2 稳定性在排序中的重要性
排序的稳定性是指在排序后，相等元素的相对顺序保持不变。对于某些应用来说，稳定性是必须的，例如在多字段排序中，先按薪资排序，薪资相同的再按姓名排序时，排序的稳定性就能保证薪资相同的记录，姓名的相对顺序不变。

## 2.3 递归排序算法的分类
递归排序算法是一类重要的排序算法，主要包括快速排序、归并排序和堆排序。它们在递归的实现方式和排序效率上有不同的特点。

### 2.3.1 快速排序和归并排序的区别
快速排序和归并排序都是分治策略的典型应用，但它们的实现方式和效率有所不同。

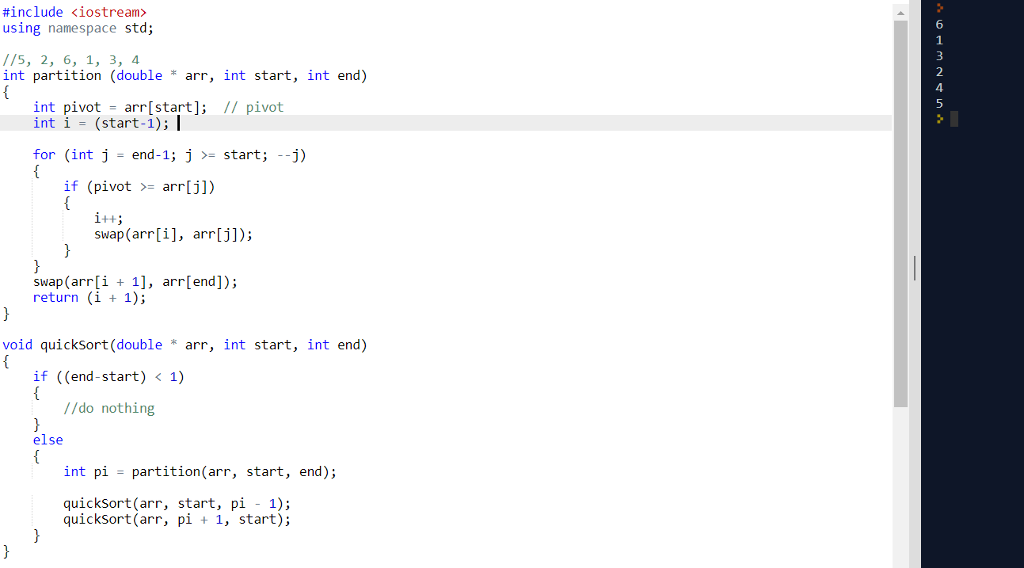
- **快速排序**：通过一个轴点（pivot）将数组分为两部分，左边部分的所有元素都不大于轴点，右边部分的所有元素都不小于轴点，然后递归排序两部分。
- **归并排序**：将数组不断分割，直到每个子数组只有一个元素，然后将这些子数组两两合并，合并过程中保持排序，直到最后只剩下一个已排序的数组。

### 2.3.2 堆排序和其他递归排序的比较
堆排序是一种基于二叉堆数据结构的排序算法，它利用堆这种数据结构的特性来进行排序。

- **堆排序**：利用堆这种数据结构所设计的一种排序算法。通过构建最大堆或最小堆，并在堆顶取值后重建堆，重复这个过程，直到堆为空。
- **与其他排序的比较**：堆排序在最坏情况下的时间复杂度与快速排序相同，但堆排序不是稳定的排序算法，且一般情况下比快速排序和归并排序有更高的常数因子，因此在实际应用中通常优先考虑快速排序和归并排序。

接下来的章节将详细介绍这些排序算法的实现和应用，以及如何优化这些算法以满足特定的需求。

# 3. 递归排序的实践演练

## 3.1 快速排序的实现和优化

### 3.1.1 快速排序的基本步骤

快速排序是一种高效的排序算法，它采用了分治法的策略。在实际应用中，快速排序因其平均时间复杂度为 O(n log n) 而被广泛使用。其基本步骤如下：

1. **选择基准值**：从数组中选择一个元素作为基准值（pivot），这个值将作为分区的依据。
2. **分区操作**：重新排列数组，所有比基准值小的元素摆放在基准前面，所有比基准值大的