【STEP7浮点数转换知识扩展】：浮点数历史背景与技术演进


参考资源链接：[西门子STEP7 32位浮点数FLOAT到64位DOUBLE转换解析](https://wenku.csdn.net/doc/6412b73dbe7fbd1778d49972?spm=1055.2635.3001.10343)
# 1. 浮点数的历史背景与重要性

在信息技术的历史长河中，浮点数的出现可谓是一次革命性的进步。计算机科学家们需要一种方法来精确地表示小数，尤其是在进行科学计算和工程设计时。浮点数的引入，不仅满足了这一需求，而且成为了现代科学计算不可或缺的一部分。

浮点数的提出，使得计算机能够处理非常大或非常小的数值，并且能以一种统一的方式表达实数。这一点在物理模拟、图形渲染、金融分析等诸多领域中都显得至关重要。

本章将概述浮点数的发展历程，讨论其对科技界的重要性，并展望浮点计算在未来可能出现的趋势和挑战。理解这些背景知识，对于在计算机科学和相关领域工作的IT专业人士而言，具有深远的意义。

# 2. ```
# 第二章：浮点数表示基础

## 2.1 浮点数的构成

### 2.1.1 符号位、指数和尾数的定义
浮点数是一种用于表示实数的方法，其核心组成部分包括符号位、指数和尾数。符号位决定了数字的正负，通常采用一位二进制数表示，0代表正数，1代表负数。指数部分相当于在科学计数法中的“10的幂次”，而在计算机中通常使用二进制指数，使得数值可以在较小的范围内变化，同时也允许数字的动态范围扩大，实现对非常大或非常小的数值的有效表示。尾数（或称为有效数字）代表了数字的有效精度，其作用类似于科学计数法中的系数。浮点数的值由这三部分共同确定，其数学表达可以简化为：

\[ (-1)^{符号位} \times 1.尾数 \times 2^{(指数 - 偏移量)} \]

这里的“偏移量”是指为了能够表示负指数而在指数位中引入的一个常数。这种结构的设计使得浮点数能够覆盖很大的数值范围，同时在表示精度上也能达到一定的要求。

### 2.1.2 IEEE标准中的浮点数格式
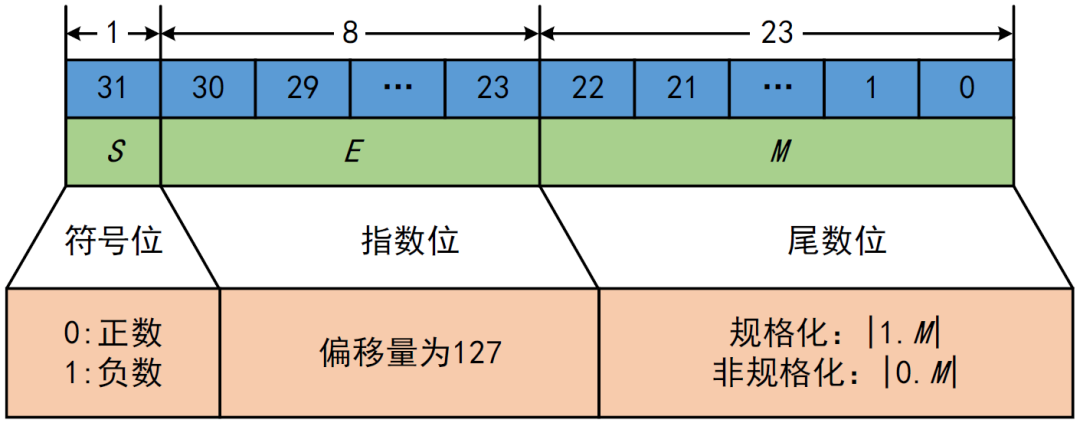
国际电工委员会（IEEE）制定了IEEE 754标准，定义了浮点数在计算机中的表示方法。最为广泛使用的是IEEE 754-1985标准，包括单精度（32位）和双精度（64位）两种格式。单精度浮点数由1位符号位、8位指数和23位尾数组成；双精度浮点数则有1位符号位、11位指数和52位尾数。

IEEE 754标准的引入使得不同计算机平台和编程语言之间的浮点数运算具有了可移植性和一致性。其对尾数的规格化和对指数的偏移量处理，还确保了浮点数运算中舍入误差的最小化。

## 2.2 浮点数的运算规则

### 2.2.1 浮点数的加法和减法运算
浮点数加法和减法是基本的运算类型，其运算过程遵循对齐指数、二进制加法、规格化和舍入等步骤。对齐指数是将两个待运算的浮点数的尾数部分右对齐，使得它们的指数部分相等。之后对尾数进行二进制加法运算，然后进行规格化（调整指数和尾数，保证尾数为左对齐并去除前导零）。最后，根据四舍五入的规则对结果尾数进行舍入处理。

### 2.2.2 浮点数的乘法和除法运算
乘法运算通常涉及尾数的乘积和指数的相加。首先，将两个浮点数的尾数相乘得到结果尾数，并将指数相加。由于乘积可能会超出规格化的范围，所以还需要进行规格化和舍入处理。除法运算则较为复杂，因为需要计算尾数的商和指数的差。除法通常要通过迭代方法逼近结果，并进行规格化和舍入处理。

### 2.2.3 浮点数的舍入和溢出处理
在执行浮点数运算时，结果可能超出了浮点数能表示的范围，即发生溢出。此外，运算结果可能无法精确表示在浮点数的尾数范围内，这时必须进行舍入处理。IEEE 754标准中定义了几种舍入模式，包括向零舍入、向上舍入、向下舍入和向最接近值舍入。

在处理溢出时，通常将结果设置为无穷大（正或负），并保留符号位。如果结果是无穷大，则会根据运算的性质返回特定的结果，例如0乘以无穷大在IEEE 754标准中是未定义的，可能会导致结果为NaN（Not-a-Number）。

接下来，我们将深入分析浮点数技术的演进历程，看看这些基础是如何随时间发展并最终确立为现代计算中不可或缺的一部分。

# 3. 浮点数技术演进历程

## 3.1 早期的浮点数表示方法

### 3.1.1 早期计算机中的浮点数表示

在计算机科学的早期发展阶段，浮点数的表示方法与现在使用的标准大相径庭。早期的计算机系统，如IBM的704型号，采用了定点表示法和早期的浮点表示法。定点表示法限制了小数点的位置，而早期的浮点表示法则没有统一的标准，各个计算机制造商使用自己的表示方法，这导致了互操作性和可移植性的问题。

浮点数的表示涉及符号位、指数和尾数三个部分。在早期的系统中，这些部分的长度和格式各不相同，计算时难以实现标准化的数学运算。这种不一致性导致软件开发人员必须为每个不同的硬件平台编写特定的代码，增加了编程的复杂性。

### 3.1.2 早期标准的发展与局限性

随着计算机技术的发展，早期的计算机制造商开始认识到标准化的重要性。这促成了某些初步的标准化尝试，例如在IBM的某些系统中，引入了统一的浮点表示方式，尽管这并没有立即获得行业内的广泛认可。

在1960年代，美国国家标准协会（ANSI）和电气和电子工程师协会（IEEE）开始制定一系列的数学和计算标准，包括浮点数的表示。但早期这些标准在实际应用中仍然存在局限性，主要是因为早期的硬件技术限制，如内存和处理器速度，以及对浮点运算的精确度和范围要求不高等因素。

## 3.2 IEEE 754标准的发展

### 3.2.1 IEEE 754标准的制定背景

为了统一不同计算机系统间浮点数的表示和运算差异，IEEE制定了IEEE 754标准，这是第一个广泛认可的浮点数运算标准。1985年发布了最初的IEEE 754标准，该标准定义了浮点数的二进制表示方式，以及在加法、减法、乘法、除法和其他运算中应遵循的规则。

IEEE 754标准的制定背景是基于对未来计算机系统发展的展望，特别是对科学计算和工程计算中浮点数运算的需求。它旨在简化和标准化浮点数的表示和运算，使得软件开发者可以在不同平台之间进行无缝移植。

### 3.2.2 IEEE 754标准的版本演进

自1985年发布以来，IEEE 754标准经历了若干次重要的更新和修订。1985年的IEEE 754-1985版本定义了单精度和双精度浮点数，后续的版本还加入了扩展精度格式，例如双扩展精度（80位）和四倍精度（128位）。

随着技术的