蚁群算法在路径规划中的应用：优化路线，提升效率，畅通出行

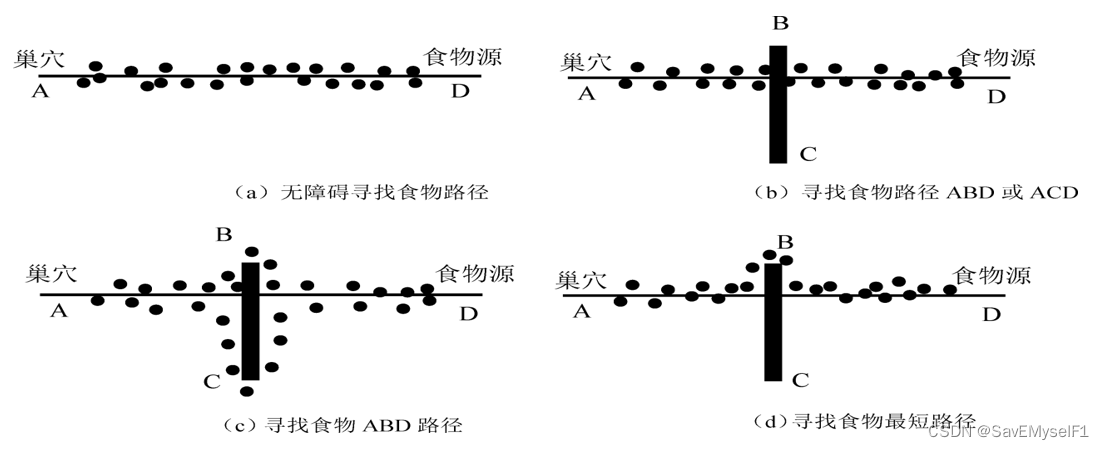
# 1. 蚁群算法基础**

蚁群算法是一种受蚂蚁觅食行为启发的优化算法。蚂蚁在觅食过程中会释放信息素，信息素越多的路径越容易被其他蚂蚁选择。蚁群算法利用这一机制来寻找最优路径。

蚁群算法的核心思想是：每个蚂蚁随机选择一条路径，然后根据路径上的信息素浓度和路径长度计算一个概率，选择概率较大的路径。随着蚂蚁的不断迭代，信息素浓度较高的路径会被更多蚂蚁选择，从而形成正反馈，最终收敛到最优路径。

# 2. 蚁群算法在路径规划中的应用

### 2.1 蚁群算法的原理和机制

蚁群算法（Ant Colony Optimization，ACO）是一种受蚂蚁觅食行为启发的优化算法。在自然界中，蚂蚁通过释放信息素来标记最佳路径，引导其他蚂蚁找到食物来源。ACO 算法模拟了这一行为，将蚂蚁视为求解器，信息素视为优化目标的度量标准。

**原理：**

1. **路径构建：**蚂蚁随机地在路径图中移动，释放信息素。
2. **信息素更新：**蚂蚁在路径上留下的信息素会随着时间的推移而蒸发。
3. **路径选择：**蚂蚁选择路径时，倾向于信息素浓度较高的路径。
4. **最优路径：**经过多次迭代后，信息素浓度最高的路径被认为是最佳路径。

### 2.2 蚁群算法在路径规划中的建模

**2.2.1 路径图的构建**

路径图是一个图结构，其中节点代表路径上的点，边代表连接这些点的路径。在路径规划中，路径图通常表示为一个加权图，其中边的权重代表路径的距离或成本。

**2.2.2 信息素的更新规则**

信息素更新规则定义了蚂蚁在路径上释放和蒸发信息素的方式。最常用的更新规则是：

τ_ij(t+1) = (1-ρ) * τ_ij(t) + Δτ_ij

其中：

* τ_ij(t) 是时间 t 时边 (i, j) 上的信息素浓度
* ρ 是信息素蒸发率
* Δτ_ij 是蚂蚁在边 (i, j) 上释放的信息素量

### 2.3 蚁群算法在路径规划中的优化策略

**2.3.1 路径选择策略**

蚂蚁选择路径时，倾向于信息素浓度较高的路径。最常用的路径选择策略是：

p_ij = τ_ij^α / ∑_k τ_ik^α

其中：

* p_ij 是蚂蚁从节点 i 移动到节点 j 的概率
* τ_ij 是边 (i, j) 上的信息素浓度
* α 是信息素权重因子

**2.3.2 信息素更新策略**

蚂蚁在路径上释放的信息素量会随着时间的推移而蒸发。最常用的信息素更新策略是：

Δτ_ij = Q / L_best

其中：

* Δτ_ij 是蚂蚁在边 (i, j) 上释放的信息素量
* Q 是常数
* L_best 是蚂蚁找到的最佳路径长度

# 3. 蚁群算法在路径规划中的实践

### 3.1 蚁群算法在交通网络中的应用

#### 3.1.1 交通网络建模

交通网络建模是将交通网络抽象成数学模型的过程，为蚁群算法的应用奠定基础。交通网络通常由节点和边组成，节点代表路口或交叉点，边代表道路或路段。

在交通网络建模中，每个节点被赋予一个坐标，表示其地理位置。每个边被赋予一个长度和一个通行时间，表示车辆通过该边的距离和时间。

#### 3.1.2 蚁群算法的求解过程

蚁群算法求解交通网络中的最短路径问题时，将蚂蚁视为在网络中移动的代理。每个蚂蚁从起点出发，随机选择下一个节点，并根据信息素和启发式信息更新信息素。

具体求解过程如下：

1. **初始化：**随机放置一定数量的蚂蚁在起点节点，并初始化信息素矩阵。
2. **蚂蚁移动：**每只蚂蚁根据信息素和启发式信息选择下一个节点，并更新信息素。
3. **信息素更新：**每只蚂蚁完成路径后，根据其路径长度更新信息素。
4. **迭代：**重复步骤 2-3，直到达到终止条件（例如，最大迭代次数或信息素收敛）。
5. **最优路径：**选择信息素最高的路径作为最优路径。

### 3.2 蚁群算法在物流配送中的应用

#### 3.2.1 物流配送网络建模

物流配送网络建模是将物流配送网络抽象成数学模型的过程，为蚁群算法的应用奠定基础。物流配送网络通常由配送中心、客户点和运输路径组成。

在物流配送网络建模中，每个配送中心被赋予一个坐标，表示其地理位置。每个客户点被赋予一个坐标，表示其地理位置。每个运输路径被赋予一个长度和一个通行时间，表示车辆通过该路径的距离和时间。

#### 3.2.2 蚁群算法的优化方案

蚁群算法求解物流配送网络中的最优配送路径问题时，将蚂蚁视为在网络中移动的代理。每个蚂蚁从配送中心出发，随机选择下一个客户点，并根据信息素和启发式信息更新信息素。

具体优化方案如下：

1. **目标函数：**最小化总配送成本，包括运输成本和时间成本。
2. **信息素更新规则：**根据蚂蚁的配送路径长度和时间更新信息素。
3. **启发式信息：**根据客户点之间的距离和时间计算启发式信息。
4. **路径选择策略：**根据信息素和启发式信息选择下一个客户点。
5. **最优配送路径：**选择信息素最高的路径作为最优配送路径。

# 4. 蚁群算法在路径规划中的进阶应用

### 4.1 蚁群算法与其他算法的融合

为了进一步提升蚁群算法在路径规划中的性能，研究人员探索了将其与其他优化算法相结合的可能性。常见的融合策略包括：

#### 4.1.1 蚁群算法与遗传算法

遗传算法（GA）是一种基于自然选择和遗传学原理的优化算法。通过将蚁群算法与遗传算法相结合，可以充分利用两者的优势。

**融合策略：**

1. 蚁群算法用于生成初始种群，遗传算法用于后续进化。
2. 蚁群算法的信息素更新机制与遗传算法的交叉和变异操作相结合。

**优势：**

* 遗传算法的全局搜索能力可以弥补蚁群算法容易陷入局部最优的缺陷。
* 蚁群算法的信息素更新机制可以指导遗传算法的搜索方向，提高收敛速度。

#### 4.1.2 蚁群算法与模拟退火算法

模拟退火算法（SA）是一种基于物理退火过程的优化算法。通过将蚁群算法与模拟退火算法相结合，可以实现更精细的搜索和避免局部最优。

**融合策略：**

1. 蚁群算法用于生成初始解，模拟退火算法用于后续优化。
2. 蚁群算法的信息素更新机制与模拟退火算法的温度退火机制相结合。

**优势：**

* 模拟退火算法的非确定性搜索能力可以帮助蚁群算法跳出局部最优。
* 蚁群算法的信息素更新机制可以为模拟退火算法提供搜索方向的参考。

### 4.2 蚁群算法在动态路径规划中的应用

在现实世界中，路径规划问题往往是动态变化的，例如交通拥堵、物流配送需求实时变化等。传统的蚁群算法难以应对动态环境下的路径规划。

#### 4.2.1 动态路径规划模型

动态路径规划模型将路径规划问题分解为一系列子问题，并逐步求解。对于动态路径规划，需要考虑以下因素：

* **状态：**路径规划过程中的当前位置和时间。
* **动作：**从当前状态到下一个状态的可选路径。
* **奖励：**执行特定动作后获得的收益（例如，时间、距离）。

#### 4.2.2 蚁群算法的实时更新机制

为了适应动态路径规划，蚁群算法需要实时更新信息素。常见的更新机制包括：

* **局部更新：**只更新当前状态下路径的信息素。
* **全局更新：**更新所有路径的信息素，反映全局路径质量的变化。
* **混合更新：**结合局部更新和全局更新，兼顾局部搜索和全局优化。

**优势：**

* 蚁群算法的实时更新机制可以快速响应环境变化，动态调整路径规划策略。
* 通过考虑时间因素，蚁群算法可以找到动态路径规划问题的最优解，满足时效性要求。

# 5.1 蚁群算法的改进与优化

蚁群算法在路径规划中取得了显著的成果，但仍存在一些可以改进和优化的方面：

- **参数优化：**蚁群算法的性能受多种参数影响，如蚂蚁数量、信息素挥发率和启发式因子。优化这些参数可以提高算法的效率和准确性。
- **路径选择策略改进：**传统的蚁群算法使用基于概率的路径选择策略，可以考虑引入更高级的策略，如精英蚂蚁策略或局部搜索策略，以提高路径质量。
- **信息素更新规则优化：**信息素更新规则是蚁群算法的核心，优化更新规则可以提高信息素的引导作用，加速算法的收敛速度。
- **并行化：**蚁群算法是一个并行算法，可以通过并行计算技术提高其效率。
- **混合算法：**将蚁群算法与其他优化算法相结合，如遗传算法或模拟退火算法，可以利用不同算法的优势，提高算法的性能。

## 5.2 蚁群算法在其他领域中的应用

蚁群算法不仅在路径规划领域取得了成功，还被广泛应用于其他领域，包括：

- **组合优化：**蚁群算法可用于解决旅行商问题、车辆路径规划问题和背包问题等组合优化问题。
- **图像处理：**蚁群算法可用于图像分割、边缘检测和纹理分析等图像处理任务。
- **数据挖掘：**蚁群算法可用于数据聚类、特征选择和关联规则挖掘等数据挖掘任务。
- **机器人导航：**蚁群算法可用于机器人导航，帮助机器人找到从起点到终点的最佳路径。
- **调度优化：**蚁群算法可用于作业调度、资源分配和时间表优化等调度优化任务。