【CVX多目标优化详解】：理论基础与实例全解析


# 摘要
CVX多目标优化是一种应用广泛的数学建模和计算框架，用于解决同时涉及多个目标的优化问题。本文首先概述了CVX多目标优化的基本概念和理论基础，包括线性、二次规划、凸优化以及Pareto优化和效率前沿等。接着，本文探讨了CVX多目标优化的算法分类，如梯度下降法、牛顿法和粒子群优化算法等，并提供了实践技巧，如CVX编程环境的搭建、多目标优化问题的建模和案例分析。文章还介绍了CVX在经济决策、工程设计和机器学习中的进阶应用，并展望了CVX多目标优化软件的发展趋势，以及在多学科交叉和开源社区中的潜在影响。

# 关键字
CVX多目标优化；线性规划；凸优化；Pareto优化；梯度下降法；粒子群优化；经济决策；工程设计；机器学习

参考资源链接：[CVX 2.2用户指南：入门与高级规则详解](https://wenku.csdn.net/doc/18dsqxx5qa?spm=1055.2635.3001.10343)
# 1. CVX多目标优化概述

在多目标优化的世界中，CVX（Conic Virtual eXtender）作为一种强大的工具，为解决多目标问题提供了一个清晰的框架。CVX是一个基于MATLAB的建模语言，它允许用户通过自然和直观的方式表述凸优化问题。这种表述方式，不仅简化了问题的构建过程，还能保证问题的凸性，从而使得求解器能够在全局范围内找到最优解。

CVX多目标优化的核心在于提供了一种语言和环境，使得复杂的多目标问题能够被方便地表达和解决。多目标优化旨在同时优化多个目标函数，这些目标函数之间往往相互冲突，因而需要找到一个平衡点，也就是所谓的Pareto最优解。CVX允许用户通过线性规划、二次规划以及更广泛的凸优化技术来处理这些问题。

CVX不仅仅是单纯的优化工具，它还提供了丰富的建模和调试功能，使得开发者和研究人员能够更快地验证理论和实验结果。在后续的章节中，我们将深入探讨CVX的理论基础、实践技巧、进阶应用以及它在不同领域的实例分析。接下来，我们将深入了解CVX优化问题的数学模型，为掌握多目标优化打下坚实的基础。

# 2. CVX多目标优化的理论基础

## 2.1 CVX优化问题的数学模型

### 2.1.1 线性规划与二次规划

线性规划（Linear Programming, LP）是优化理论中最基本的模型之一，广泛应用于资源分配、生产计划和金融投资等领域。它涉及的是线性函数的最优化问题，在一定线性约束条件下求解线性目标函数的最大值或最小值。二次规划（Quadratic Programming, QP）是线性规划的扩展，其目标函数是二次的，而约束条件依然是线性的。

在CVX中，线性规划和二次规划的问题可以这样表示：

cvx_begin
    variable x(n)
    minimize (c' * x)
    subject to
        A * x <= b
        x >= 0
cvx_end

这里 `c` 是目标函数系数向量，`A` 和 `b` 是定义不等式约束的矩阵和向量，`x` 是需要优化的变量向量。对于二次规划，目标函数会包含二次项 `x'*P*x`，其中 `P` 是半正定矩阵。

### 2.1.2 凸优化的基本概念

凸优化问题是指目标函数为凸函数，并且约束条件定义的可行域为凸集的优化问题。凸优化的一个关键特性是局部最小值同时也是全局最小值，这为找到最优解提供了便利。

凸集是指在集合内任意两点连线上的所有点都属于该集合的情况。凸函数则是指在定义域内任意两点连线上的函数值都不大于这两点函数值的连线，即对于函数 `f(x)`，对于任意的 `x1, x2` 和 `θ` 满足 `0 ≤ θ ≤ 1`，都有 `f(θx1 + (1-θ)x2) ≤ θf(x1) + (1-θ)f(x2)`。

CVX在求解凸优化问题时，利用了这些数学理论的性质以保证求解的全局最优性。实际使用CVX时，用户无需手动证明问题的凸性，CVX会自动进行检查，并在问题非凸时给出警告。

## 2.2 CVX多目标优化原理

### 2.2.1 Pareto优化和效率前沿

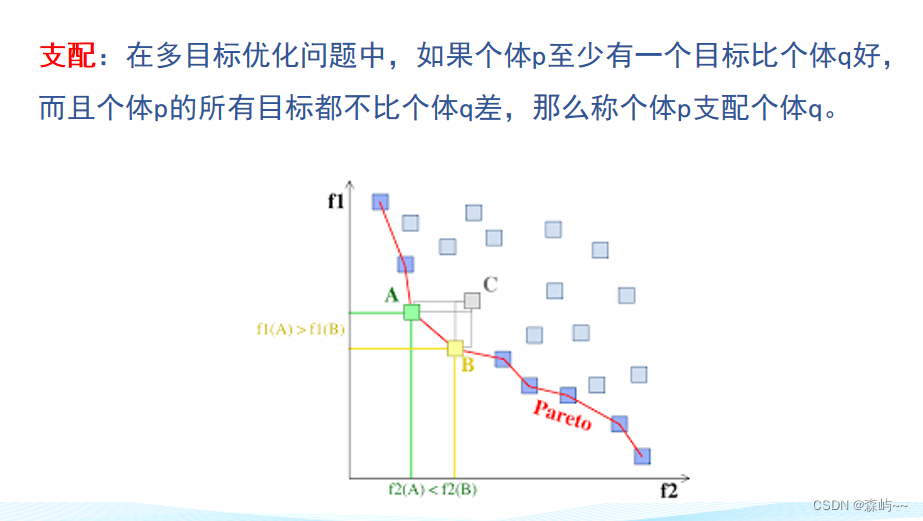
多目标优化问题中，由于涉及到多个相互矛盾的目标函数，很难找到一个解同时最优化所有目标。Pareto优化是一种处理多目标问题的方法，其核心是寻找一组解，这些解之间无法通过改变决策变量的方式同时改进所有目标。

这组解称为Pareto最优解集，而由Pareto最优解集构成的表面称为效率前沿（Efficient Frontier）。效率前沿表示了在当前问题和约束条件下，各目标之间的最佳权衡。

### 2.2.2 权重法与约束法

在多目标优化问题中，权衡不同目标的相对重要性是关键，权重法和约束法是常用的两种策略。

- 权重法：通过为每个目标函数分配权重，将多目标问题转化为单目标问题。权衡的困难在于权重的选择很大程度上依赖于决策者的主观判断，并且可能需要尝试多个权重组合来获取满意的解集。

- 约束法：这种方法将部分目标函数转换为约束条件，仅优化剩余的目标函数。它允许决策者直观地控制特定目标的性能，但可能导致某些目标的性能变得非常差。

## 2.3 CVX多目标优化的算法分类

### 2.3.1 梯度下降法与牛顿法

梯度下降法是求解优化问题的一种基本迭代方法，其核心思想是沿着目标函数梯度的反方向更新解。在多目标优化中，这个方法需要被适当地修改以适应多目标的环境。

牛顿法是一种基于二阶导数的优化算法，通过构建目标函数的二次模型来寻找最小值点。尽管牛顿法在单目标优化中非常有效，但在多目标优化中的应用较为有限，主要原因是多目标优化中难以构建一个合适的多维二次模型。

### 2.3.2 粒子群优化算法

粒子群优化（Particle Swarm Optimization, PSO）是一种模仿鸟群捕食行为的群体智能优化算法。在多目标版本的PSO中，每个粒子不再仅仅追求一个解，而是代表一个可能的Pareto最优解。

多目标PSO通过维护一个解集来代表Pareto前沿，并不断地更新粒子位置和速度，以此来改进解集的质量。算法的收敛性和多样性保持是多目标PSO研究的关键点。

以上内容详细地介绍了CVX多目标优化的基础理论，通过构建模型、应用算法以及实现技巧，可以对复杂的多目标优化问题进行建模和求解。在接下来的章节中，我们将进一步深入到CVX多目标优化实践技巧中，了解如何搭建CVX编程环境、建模并分析案例。

# 3. CVX多目标优化实践技巧

## 3.1 CVX编程环境的搭建

### 3.1.1 CVX安装与配置

在进行CVX多目标优化之前，首先需要一个适合的编程环境。CVX是一个基于MATLAB的软件包，用于建模和解决凸优化问题。安装CVX的过程相对简单，以下是步骤详解：

1. **下载CVX**：前往CVX官网下载最新版本的CVX。确保下载对应的操作系统和MATLAB版本。

2. **安装CVX**：下载完成后，按照MATLAB的Add-Ons Manager进行安装，或者在MATLAB命令窗口输入`cvx_setup`，然后按照指引完成安装。

3. **环境配置**：安装完毕后，需要将CVX添加到MATLAB的路径中。在MATLAB命令窗口输入`addpath`函数并指定CVX安装的路径。

4. **验证安装**：安装完成后，可以通过输入`cvx_version`命令来验证CVX是否正确安装，并且确保输出的版本号是正确的。

安装和配置CVX环境是后续实践的基础，需要确保每一步都正确执行，以避免在优化过程中出现不必要的错误。

### 3.1.2 CVX的使用界面和基本命令

CVX提供了一个简洁的使用界面，使得用户可以以一种非常直观的方式构建和解决优化问题。下面介绍CVX的一些基本命令和操作：

1. **问题定义**：首先，用户需要定义优化问题的目标函数和约束条件。CVX将MATLAB的语法和数学逻辑进行了整合，用户可以使用MATLAB的语法来表达这些内容。

2. **模型求解**：在定义好问题之后，使用`cvx_begin`和`cvx_end`命令对问题求解。在这两个命令之间放置优化问题的相关命令。

3. **结果输出**：问题求解完成后，可以使用`cvx_status`查看求解状态，`cvx_optval`获取优化目标函数的最优值，以及`cvx_solution`查看解的详细信息。

4. **模型调试**：如果问题定义不当，求解器可能无法找到解决方案。CVX提供了检查功能，用户可以通过`cvx_check`命令来验证问题定义是否符合凸优化的要求。

这些是CVX的基本命令和界面操作，它们为用户提供了强大的工具来实现复杂的优化模型。

## 3.2 CVX多目标优化问题的建模

### 3.2.1 问题定义与约束表达

在CVX中建模多目标优化问题，首先需要对问题进行准确的数学定义，包括目标函数和约束条件。下面