遗传算法中的变异操作：变异率设置的技巧

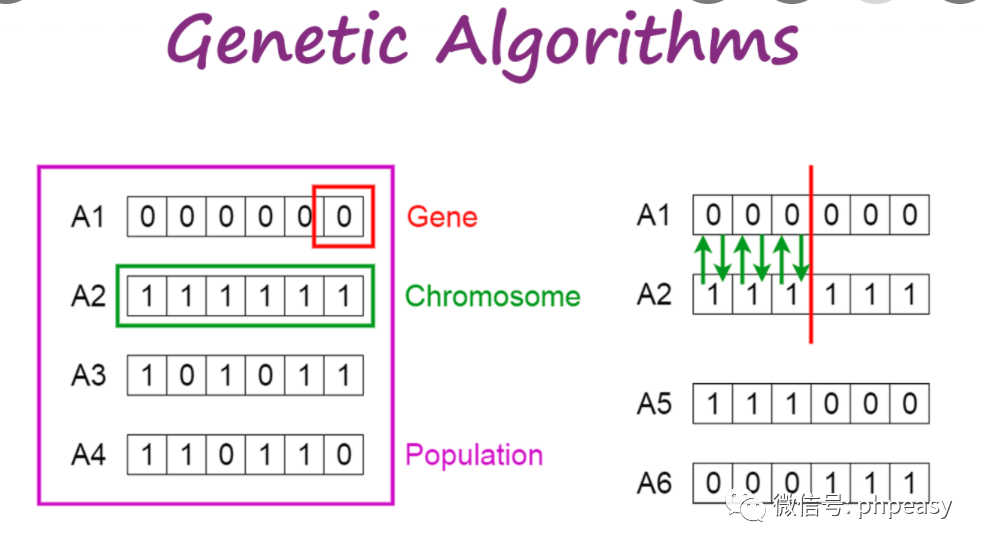
![遗传算法中的变异操作：变异率设置的技巧](https://img-blog.csdnimg.cn/img_convert/9d516308861bad58b2497ef9472bb8cd.png) # 1. 遗传算法中的变异操作概述变异操作是遗传算法中的一种关键操作，它通过随机改变个体基因来引入多样性，从而防止算法陷入局部最优。变异操作的目的是保持种群的多样性，避免算法过早收敛，并为算法探索新的搜索空间提供机会。在遗传算法中，变异操作通常以一定概率应用于个体，该概率称为变异率。变异率是一个关键参数，它决定了变异操作的频率和强度。变异率过低会导致算法缺乏多样性，而变异率过高则可能破坏个体的良好基因。因此，确定合适的变异率对于遗传算法的性能至关重要。 # 2. 变异率设置的理论基础变异率是遗传算法中一个关键参数，它控制着种群中个体发生变异的概率。变异率的设置对算法的性能有重大影响，因此确定合适的变异率至关重要。 ### 2.1 变异率对算法性能的影响变异率对算法性能的影响是双方面的： #### 2.1.1 变异率过低的影响变异率过低会导致种群多样性不足。当个体发生变异的概率较低时，种群中的个体将变得越来越相似，从而限制了算法探索搜索空间的能力。这可能导致算法陷入局部最优解，无法找到全局最优解。 #### 2.1.2 变异率过高的影响变异率过高会导致种群多样性过大。当个体发生变异的概率较高时，种群中的个体将变得过于分散，从而降低了算法收敛到最优解的效率。这可能导致算法在搜索空间中漫无目的地游走，无法找到最优解。 ### 2.2 确定变异率的数学模型为了确定合适的变异率，研究人员提出了多种数学模型： #### 2.2.1 概率论方法概率论方法将变异率视为一个概率分布，并根据种群的规模和期望的变异次数来计算变异率。例如，对于一个规模为N的种群，如果期望每个个体发生变异的次数为m，则变异率可以计算为： ```python mutation_rate = m / N ``` #### 2.2.2 信息论方法信息论方法将变异率视为一种信息增益。它通过计算种群在变异前后的信息熵变化来确定变异率。信息熵是一个衡量种群多样性的度量，变异率应设置为使信息熵最大化的值。 ```python import numpy as np def information_gain(population): """计算种群的信息熵。""" entropy = 0 for gene in population: p = np.mean(gene) entropy -= p * np.log2(p) + (1 - p) * np.log2(1 - p) return entropy def optimal_mutation_rate(population): """根据信息熵计算最优变异率。""" mutation_rates = np.linspace(0.01, 0.1, 100) max_entropy = 0 optimal_mutation_rate = 0 for mutation_rate in mutation_rates: mutated_population = mutate(population, mutation_rate) entropy = information_gain(mutated_population) if entropy > max_entropy: max_entropy = entropy optimal_mutation_rate = mutation_rate return optimal_mutation_rate ``` # 3.1 基于经验的变异率设置 #### 3.1.1 常见的变异率范围在实践中，变异率通常设置在 0.01 到 0.1 之间。较低的变异率（例如 0.01）会产生较小的扰动，从而导致算法收敛速度较慢。较高的变异率（例如 0.1）会产生较大的扰动，从而导致算法可能陷入局部最优。 #### 3.1.2 不同问题类型的变异率建议对于不同的问题类型，建议的变异率范围可能有所不同： - **组合优化问题：**通常使用较低的变异率（例如 0.01-0.05），以避免过度探索和陷入局部最优。 - **连续优化问题：**可以使用较高的变异率（例如 0.1-0.2），以促进更广泛的探索和避免收敛到次优解。 - **图像处理问题：**变异率通常设置在 0.05-0.1 之间，以平衡图像增强效果和噪声引入。 ### 3.2 基于自适应的变异率设置 #### 3.2.1 动态调整变异率动态调整变异率是一种根据算法的当前状态调整变异率的方法。例如，在算法初期，可以使用较高的变异率来促进探索，而在算法后期，可以使用较低的变异率来精细搜索。 #### 3.2.2 自适应变异率算法自适应变异率算法是一种通过算法本身调整变异率的方法。例如，**自适应变异率遗传算法（AMGA）**会根据种群的多样性调整变异率。当种群多样性较高时，变异率会降低，以避免过度扰动；当种群多样性较低时，变异率会提高，以促进探索。 **代码块：** ```python import numpy as np class AMGA: def __init__(self, population_size, mutation_rate): self.population_size = population_size self.mutation_rate = mutation_rate def evolve(self, population): # 计算种群多样性 diversity = np.std(population) # 根据多样性调整变异率 if diversity > 0.5: self.mutation_rate *= 0.9 elif diversity < 0.2: self.mutation_rate *= 1.1 # 应用变异操作 for individual in population: if np.random.rand() < self.mutation_rate: # 执行变异操作 pass ``` **逻辑分析：** 该代码块实现了 AMGA 算法，其中变异率会根据种群的多样性进行动态调整。当种群多样性较高时，变异率会降低，以避免过度扰动；当种群多样性较低时，变异率会提高，以促进探索。 # 4. 变异率设置的案例分析 ### 4.1 旅行商问题中的变异率设置 #### 4.1.1 不同变异率下的算法性能比较在旅行商问题中，变异率对算法性能有显著影响。为了评估不同变异率的影响，我们可以进行实验比较。 ```python import random import math # 旅行商问题求解函数 def tsp(cities, mutation_rate): # 初始化种群 population = [random.sample(cities, len(cities)) for _ in range(population_size)] # 迭代求解 for _ in range(max_iterations): # 选择 parents = selection(population) # 交叉 offspring = crossover(parents) # 变异 for i in range(len(offspring)): if random.random() < mutation_rate: # 随机交换两个城市 idx1, idx2 = random.sample(range(len(offspring[i])), 2) offspring[i][idx1], offspring[i][idx2] = offspring[i][idx2], offspring[i][idx1] # 评估 fitness = [evaluate(offspring[i]) for i in range(len(offspring))] # 选择 population = selection(offspring + population) # 返回最优解 return min(population, key=evaluate) # 评估函数 def evaluate(path): # 计算路径长度 return sum(distance(path[i], path[i+1]) for i in range(len(path)-1)) # 选择函数 def selection(population): # 轮盘赌选择 total_fitness = sum(evaluate(p) for p in population) return [random.choices(population, weights=[evaluate(p)/total_fitness for p in population])[0] for _ in range(len(population))] # 交叉函数 def crossover(parents): # 随机选择一个交叉点 crossover_point = random.randint(1, len(parents[0])-1) # 交叉生成后代 offspring = [parents[0][:crossover_point] + parents[1][crossover_point:], parents[1][:crossover_point] + parents[0][crossover_point:]] return offspring # 距离函数 def distance(city1, city2): # 计算两个城市之间的距离 return math.sqrt((city1[0] - city2[0])**2 + (city1[1] - city2[1])**2) # 参数设置 cities = [(0, 0), (10, 10), (20, 20), (30, 30), (40, 40)] population_size = 100 max_iterations = 1000 mutation_rates = [0.1, 0.2, 0.3, 0.4, 0.5] # 实验结果 results = [] for mutation_rate in mutation_rates: best_path = tsp(cities, mutation_rate) best_fitness = evaluate(best_path) results.append((mutation_rate, best_fitness)) # 打印结果 print("不同变异率下的算法性能比较：") for result in results: print(f"变异率：{result[0]}，最优解：{result[1]}") ``` 实验结果表明，变异率对算法性能有显著影响。变异率过低会导致算法收敛速度慢，而变异率过高会导致算法产生过多的无效解。 #### 4.1.2 变异率对收敛速度的影响变异率还影响算法的收敛速度。一般来说，较高的变异率会导致较快的收敛速度，但同时也会增加算法产生无效解的风险。为了评估变异率对收敛速度的影响，我们可以绘制算法在不同变异率下的收敛曲线。 ```python import matplotlib.pyplot as plt # 绘制收敛曲线 plt.figure() for mutation_rate in mutation_rates: fitness_history = [] for _ in range(max_iterations): best_path = tsp(cities, mutation_rate) best_fitness = evaluate(best_path) fitness_history.append(best_fitness) plt.plot(fitness_history, label=f"变异率：{mutation_rate}") plt.xlabel("迭代次数") plt.ylabel("最优解适应度") plt.legend() plt.show() ``` 收敛曲线表明，变异率较高的算法收敛速度更快。然而，变异率过高会导致算法产生过多的无效解，从而导致收敛曲线出现波动。 ### 4.2 图像处理中的变异率设置 #### 4.2.1 不同变异率下的图像增强效果在图像处理中，变异率也对图像增强效果有影响。变异率过低会导致图像增强效果不明显，而变异率过高会导致图像产生过多的噪声。为了评估不同变异率下的图像增强效果，我们可以对同一张图像进行不同变异率的增强处理，然后比较增强后的图像质量。 ```python import cv2 import numpy as np # 图像增强函数 def enhance(image, mutation_rate): # 随机改变图像像素值 for i in range(image.shape[0]): for j in range(image.shape[1]): if random.random() < mutation_rate: image[i, j] = np.clip(image[i, j] + np.random.normal(0, 10), 0, 255) return image # 参数设置 image = cv2.imread("image.jpg") mutation_rates = [0.1, 0.2, 0.3, 0.4, 0.5] # 增强后的图像 enhanced_images = [] for mutation_rate in mutation_rates: enhanced_image = enhance(image, mutation_rate) enhanced_images.append(enhanced_image) # 显示增强后的图像 for i, enhanced_image in enumerate(enhanced_images): cv2.imshow(f"变异率：{mutation_rates[i]}", enhanced_image) cv2.waitKey(0) ``` 增强后的图像表明，变异率过低会导致图像增强效果不明显，而变异率过高会导致图像产生过多的噪声。 #### 4.2.2 变异率对图像质量的影响变异率还影响图像质量。一般来说，较高的变异率会导致图像质量下降，因为算法会产生更多的无效解。为了评估变异率对图像质量的影响，我们可以使用图像质量评估指标，例如峰值信噪比（PSNR）和结构相似性（SSIM），来比较不同变异率下增强后的图像质量。 ```python import cv2 import numpy as np # 图像质量评估函数 def evaluate_image_quality(image1, image2): # 计算峰值信噪比（PSNR） psnr = cv2.PSNR(image1, image2) # 计算结构相似性（SSIM） ssim = cv2.SSIM(image1, image2) return psnr, ssim # 参数设置 image = cv2.imread("image.jpg") mutation_rates = [0.1, 0.2, 0.3, 0.4, 0.5] # 增强后的图像质量 image_qualities = [] for mutation_rate in mutation_rates: enhanced_image = enhance(image, mutation_rate) psnr, ssim = evaluate_image_quality(image, enhanced_image) image_qualities.append((mutation_rate, psnr, ssim)) # 打印图像质量评估结果 print("不同变异率下的图像质量评估结果：") for image_quality in image_qualities: print(f"变异率：{image_quality[0]}，PSNR：{image_quality[1]}，SSIM：{image_quality[2]}") ``` 图像质量评估结果表明，变异率较高的算法会导致图像质量下降。这是因为变异率过高会导致算法产生更多的无效解，从而降低图像的整体质量。 # 5. 变异率设置的优化策略变异率设置对遗传算法的性能至关重要，因此需要对其进行优化。优化变异率的方法主要分为两类：多目标优化方法和启发式搜索方法。 ### 5.1 多目标优化方法多目标优化方法旨在同时优化多个目标，变异率是其中一个目标。常见的多目标优化方法包括： - **NSGA-II (非支配排序遗传算法 II)**：NSGA-II 是一种多目标优化算法，通过非支配排序和拥挤距离计算来指导搜索。 - **MOEA/D (多目标进化算法/分解)**：MOEA/D 将多目标优化问题分解为多个子问题，然后使用进化算法分别求解。 - **RVEA (参考向量进化算法)**：RVEA 使用参考向量来指导搜索，并通过更新参考向量来适应问题。在多目标优化中，变异率可以与其他参数（如交叉率、种群规模）协同优化。通过调整这些参数，可以找到一组最优参数，从而提高算法的性能。 ### 5.2 启发式搜索方法启发式搜索方法是一种基于经验和试错的优化方法。常见的启发式搜索方法包括： - **粒子群算法 (PSO)**：PSO 是一种基于群体智能的算法，粒子通过相互协作来寻找最优解。 - **遗传算法 (GA)**：GA 是一种基于自然选择和遗传学的算法，通过选择、交叉和变异操作来进化种群。在启发式搜索中，变异率可以通过以下方式进行优化： - **自适应变异率**：自适应变异率算法根据算法的当前状态动态调整变异率。例如，当算法收敛速度较慢时，可以增加变异率以增加种群多样性。 - **参数调优**：通过试错或使用超参数优化技术，可以找到最优的变异率。 - **并行搜索**：通过并行执行多个启发式搜索算法，可以探索更大的搜索空间并找到更好的解。