：单片机舵机控制与PID算法：精准控制，稳定运行，揭秘调参秘籍

# 1. 单片机舵机控制基础

舵机是一种将电信号转换为角位移的执行器，广泛应用于机器人、智能车等领域。单片机舵机控制涉及舵机驱动电路设计、单片机控制程序设计以及PID算法应用。

### 1.1 舵机的工作原理

舵机内部有一个电机，通过齿轮减速后带动输出轴转动。通过控制电机的转动方向和时间，可以实现舵机的角度控制。舵机的控制信号一般为脉宽调制（PWM）信号，其中脉宽的长度决定了舵机的转动角度。

### 1.2 舵机驱动电路设计

舵机驱动电路主要包括功率放大器和反馈电路。功率放大器负责放大单片机的PWM信号，驱动舵机的电机。反馈电路用于检测舵机的实际转动角度，并将其反馈给单片机进行控制。

# 2. PID算法原理与应用

### 2.1 PID算法的理论基础

#### 2.1.1 比例、积分、微分控制原理

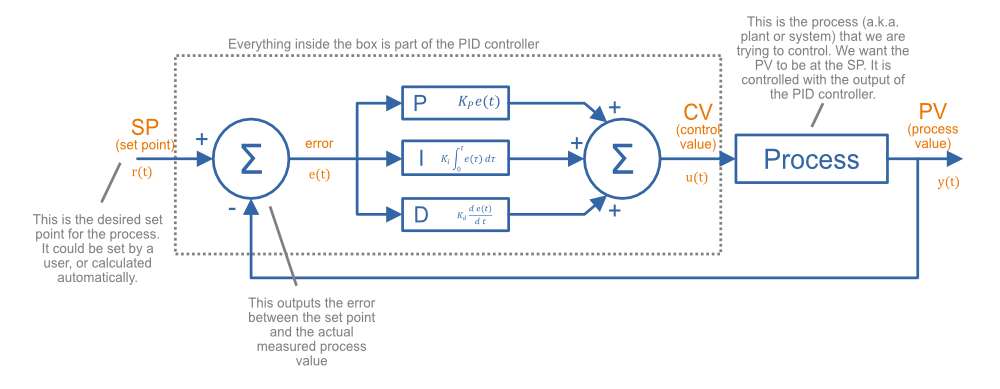
PID算法（比例-积分-微分算法）是一种反馈控制算法，广泛应用于各种工业自动化和机器人控制系统中。PID算法通过调整比例（P）、积分（I）和微分（D）三个参数来控制系统的输出。

* **比例控制：**根据当前误差的大小进行控制，误差越大，控制输出越大。
* **积分控制：**根据误差的累积值进行控制，误差累积越多，控制输出越大。
* **微分控制：**根据误差变化率进行控制，误差变化率越大，控制输出越大。

#### 2.1.2 PID算法的数学模型

PID算法的数学模型为：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* `u(t)`：控制输出
* `e(t)`：误差（期望值与实际值之差）
* `Kp`：比例系数
* `Ki`：积分系数
* `Kd`：微分系数

### 2.2 PID算法的调参方法

PID算法的调参是至关重要的，它直接影响系统的控制性能。常用的调参方法包括：

#### 2.2.1 常用调参方法介绍

* **齐格勒-尼科尔斯法：**基于系统的阶跃响应，通过测量系统上升时间和峰值时间来确定PID参数。
* **Cohen-Coon法：**基于系统的过程增益和时间常数来确定PID参数。
* **经验调参法：**根据经验和试错来调整PID参数。

#### 2.2.2 调参经验分享

* **比例系数Kp：**从较小的值开始逐渐增大，直到系统出现振荡，然后减小Kp。
* **积分系数Ki：**从较小的值开始逐渐增大，直到系统响应变慢，然后减小Ki。
* **微分系数Kd：**从较小的值开始逐渐增大，直到系统出现超调，然后减小Kd。

### 2.3 PID算法的仿真与验证

#### 2.3.1 仿真平台搭建

可以使用MATLAB、Simulink等仿真平台搭建PI