数据结构课程设计：用JOSEPH环解决实际问题的策略与技巧


# 摘要
JOSEPH环问题作为算法研究的经典案例，涉及到多种算法原理和编程实现的挑战。本文首先阐述了JOSEPH环问题的理论基础，并提供了环形结构的数学模型和基本算法步骤。接着，本文深入探讨了解决JOSEPH环问题的策略，包括对问题复杂度的分析和策略选择标准。在编程实践部分，文章比较了不同编程语言特性，并选择了最适合语言实现JOSEPH环算法，同时强调了代码测试与调试的重要性。通过实际应用案例的分析，展示了JOSEPH环问题解决方案的设计与实施过程以及应用效果的评估与优化。最后，本文对JOSEPH环问题的变种与挑战进行了讨论，并对未来技术发展趋势及教学启示提出了建议。

# 关键字
JOSEPH环；算法原理；编程实现；问题复杂度；代码测试；技术趋势

参考资源链接：[单循环链表实现约瑟夫环课程设计](https://wenku.csdn.net/doc/73tx0bchf8?spm=1055.2635.3001.10343)
# 1. JOSEPH环问题的理论基础

JOSEPH环问题，源自于约瑟夫·傅立叶提出的数学问题，属于典型的递归算法应用场景。问题的本质是模拟一组人围成一圈，按照指定数目的规则进行递减选择，最终只剩下一人或一组人。这一问题在图论、数据结构以及算法理论中具有重要意义，是研究数据结构中的循环链表和递归概念的基础。

在理解JOSEPH环问题的理论基础时，我们需要清楚以下几个关键点：
- **问题的由来与定义**：了解问题的历史背景以及其数学和计算机科学上的定义。
- **核心概念**：掌握循环链表、递归等数据结构和算法中的基本概念。

### 2.1 JOSEPH环问题的算法描述

#### 2.1.1 环形结构的数学模型

JOSEPH环问题的数学模型可以看作是一个封闭的环形结构，其中每一点代表一个人，每经过一次迭代，就会根据规则排除一个人，直到只剩下最后一个人。

#### 2.1.2 基本算法步骤

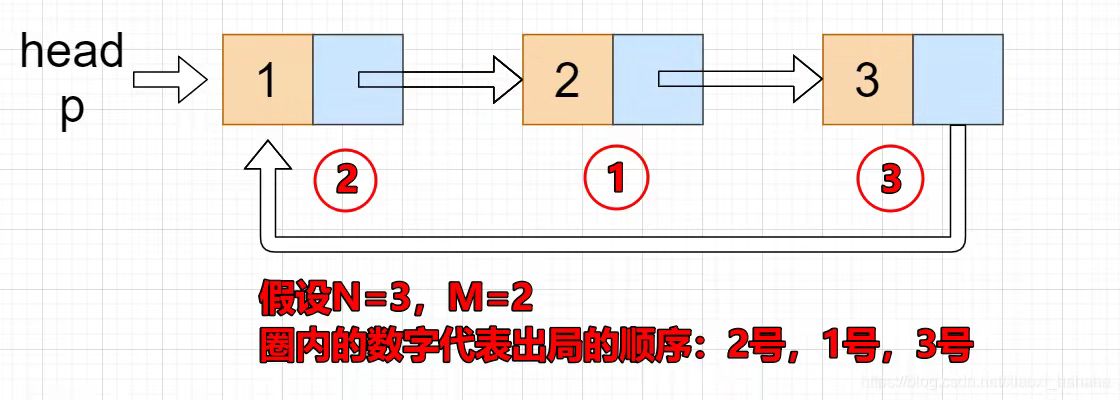
- **初始化**：定义一个代表人数的变量N，以及一个代表每次排除人数的变量M。
- **迭代过程**：从第一个位置开始，每次移动M-1个位置进行排除，直到剩下一个人。
- **返回结果**：返回最后剩下的那个人的位置信息或编号。

通过这样的基本算法步骤，我们可以清晰地理解JOSEPH环问题的核心算法流程。下文将对解决JOSEPH环问题的策略进行深入探讨，并介绍实际的编程实践案例。

# 2. 解决JOSEPH环问题的策略

## 2.1 JOSEPH环问题的算法描述
### 2.1.1 环形结构的数学模型
JOSEPH环问题，也被称为约瑟夫斯问题（Josephus Problem），源自一个古老的故事。在这个故事中，一群人围成一个圈，每数到第k个人，这个就被排除出圈外。然后从下一个人开始继续数数，直到所有人都被排除为止。数学上，这个问题通常用一个环形结构来模拟，即一组对象排列成一个圈，并且进行删除操作直到只剩下一个对象。

环形结构可以通过一系列的数学模型来描述。考虑一组编号为1到n的元素，这些元素排成一个圆圈。从第一个人开始数，每数到第k个人时，这个被移除，然后从下一个人开始继续这个过程。数学上，这个问题可以通过递归或迭代的算法来解决。

### 2.1.2 基本算法步骤
解决JOSEPH环问题的基本算法可以分为以下步骤：

1. 创建一个包含所有元素的列表。
2. 设置一个计数器，从第一个人开始计数，每次增加1，直到达到k。
3. 当计数器达到k时，删除当前计数器指向的元素。
4. 重置计数器，从下一个元素开始继续计数。
5. 重复步骤3和4，直到列表中只剩下一个元素。
6. 输出最后剩下的元素。

## 2.2 解决JOSEPH环问题的策略分析
### 2.2.1 问题的复杂度分析
解决JOSEPH环问题的算法复杂度主要取决于列表中元素的数量n，以及每次数数的间隔k。在最简单的实现中，我们可以通过一个双端队列（deque）来模拟这个过程，每次删除操作的时间复杂度为O(1)。因此，整体算法的时间复杂度为O(n)，这是因为每个元素都会被删除一次。

空间复杂度相对简单，为O(n)，因为我们需要存储所有的元素。不过，在一些优化的实现中，空间复杂度可以被降低，例如通过循环数组或者数学公式直接计算结果。

### 2.2.2 策略选择标准
在多种策略中选择解决JOSEPH环问题的方法时，需要考虑以下标准：

- **算法的简洁性**：优先选择实现简单、易于理解的策略。
- **效率**：在处理大数据集时，选择时间复杂度和空间复杂度都较低的策略。
- **可扩展性**：策略应该可以处理不同的n和k值，甚至在某些情况下能够处理变化的k值（动态JOSEPH环问题）。
- **通用性**：选择可以用于多种编程语言和平台的策略，以便在不同的项目中重用。

接下来，让我们深入探讨在实际应用中解决JOSEPH环问题的编程实践。

# 3. JOSEPH环问题的编程实践

## 3.1 JOSEPH环问题的编程语言选择

### 3.1.1 语言特性对比