Python列表操作的算法解析：append()函数的时间和空间复杂度

# 1. Python列表的基本概念和操作

Python列表是一种有序、可变的数据结构，用于存储一系列元素。列表元素可以是任何数据类型，包括其他列表。列表可以通过方括号 `[]` 创建，元素之间用逗号分隔。

列表提供了丰富的操作方法，包括添加、删除、插入和排序元素。其中，`append()` 函数用于在列表末尾添加元素，`insert()` 函数用于在指定位置插入元素，`remove()` 函数用于删除特定元素，`sort()` 函数用于对列表元素进行排序。

# 2. Python列表操作算法的复杂度分析

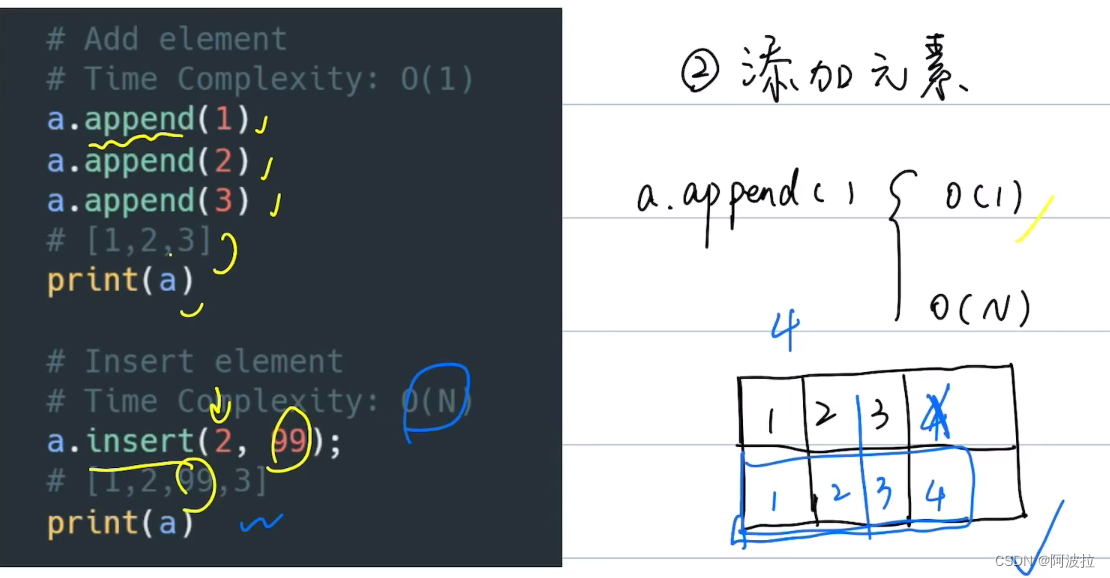
### 2.1 append()函数的时间复杂度

#### 2.1.1 最好情况下的时间复杂度

在最好情况下，当列表为空或列表末尾有足够的空间容纳新元素时，append()函数的时间复杂度为O(1)。这是因为在这些情况下，Python只需将新元素添加到列表的末尾，而无需重新分配内存。

# 最好情况：列表为空或末尾有足够的空间
my_list = []
my_list.append(1)  # 时间复杂度为 O(1)

#### 2.1.2 最坏情况下的时间复杂度

在最坏情况下，当列表已满且需要重新分配内存时，append()函数的时间复杂度为O(n)。这是因为Python必须创建一个新列表，将现有元素复制到新列表中，然后将新元素添加到新列表的末尾。

# 最坏情况：列表已满，需要重新分配内存
my_list = [1, 2, 3, 4, 5]
my_list.append(6)  # 时间复杂度为 O(n)

#### 2.1.3 平均情况下的时间复杂度

在平均情况下，append()函数的时间复杂度为O(1)。这是因为在大多数情况下，列表末尾都有足够的空间容纳新元素，不需要重新分配内存。

### 2.2 append()函数的空间复杂度

#### 2.2.1 最好情况下的空间复杂度

在最好情况下，当列表为空或列表末尾有足够的空间容纳新元素时，append()函数的空间复杂度为O(1)。这是因为在这些情况下，Python无需分配额外的内存。

#### 2.2.2 最坏情况下的空间复杂度

在最坏情况下，当列表已满且需要重新分配内存时，append()函数的空间复杂度为O(n)。这是因为Python必须创建一个新列表，其大小是原列表大小的两倍。

#### 2.2.3 平均情况下的空间复杂度

在平均情况下，append()函数的空间复杂度为O(1)。这是因为在大多数情况下，列表末尾都有足够的空间容纳新元素，不需要重新分配内存。

### 2.3 时间复杂度分析总结

| 操作 | 最好情况 | 最坏情况 | 平均情况 |
|---|---|---|---|
| append() | O(1) | O(n) | O(1) |

**注：**

* n表示列表的长度。
* 时间复杂度分析基于Python 3.10。

# 3. Python列表操作算法的优化技巧

### 3.1 减少列表复制

在Python中，列表是可变的，这意味着它们可以被修改。当对列表进行修改时，Python会创建一个新的列表对象，并将修改后的元素存储在其中。这个过程称为列表复制。列表复制是一个耗时的操作，尤其是在列表很大的情况下。

为了减少列表复制，我们可以使用以下技巧：

#### 3.1.1 使用切片操作

切片操作可以创建一个列表的副本，而无需复制整个列表。切片操作使用以下语法：

new_list = old_list[start:end]

其中：

* `old_list` 是要创建副本的列表。
* `start` 是切片的开始索引（包括在内）。
* `end` 是切片的结束索引（不包括在内）。

例如，以下代码创建一个 `old_list` 列表的副本，其中包含索引 1 到 4（不包括 4）之间的元素：

old_list = [1, 2, 3, 4, 5]
new_list = old_list[1:4]
print(new_list)  # 输出：[2, 3, 4]

#### 3.1.2 使用列表推导式

列表推导式是一种创建列表的简洁方式，而无需显式地复制列表。列表推导式使用以下语法：

new_list = [expression for item in ol