MATLAB方程求解的案例研究：展示现实世界的应用，让你学以致用

# 1. MATLAB方程求解的基础**

MATLAB是一种强大的数值计算环境，可用于求解各种方程。方程求解是MATLAB中一项基本任务，可用于各种应用，例如数据拟合、优化和建模。

在本章中，我们将介绍MATLAB方程求解的基础知识，包括：

* MATLAB中方程求解的语法和函数
* 数值分析方法，例如牛顿-拉夫逊法和梯度下降法
* MATLAB中方程求解函数的优缺点

# 2. 方程求解的理论基础**

**2.1 数值分析方法**

数值分析方法是一种通过计算机来求解数学问题的技术。在方程求解中，数值分析方法可以将方程转化为一系列可以逐步求解的近似问题。常用的数值分析方法包括：

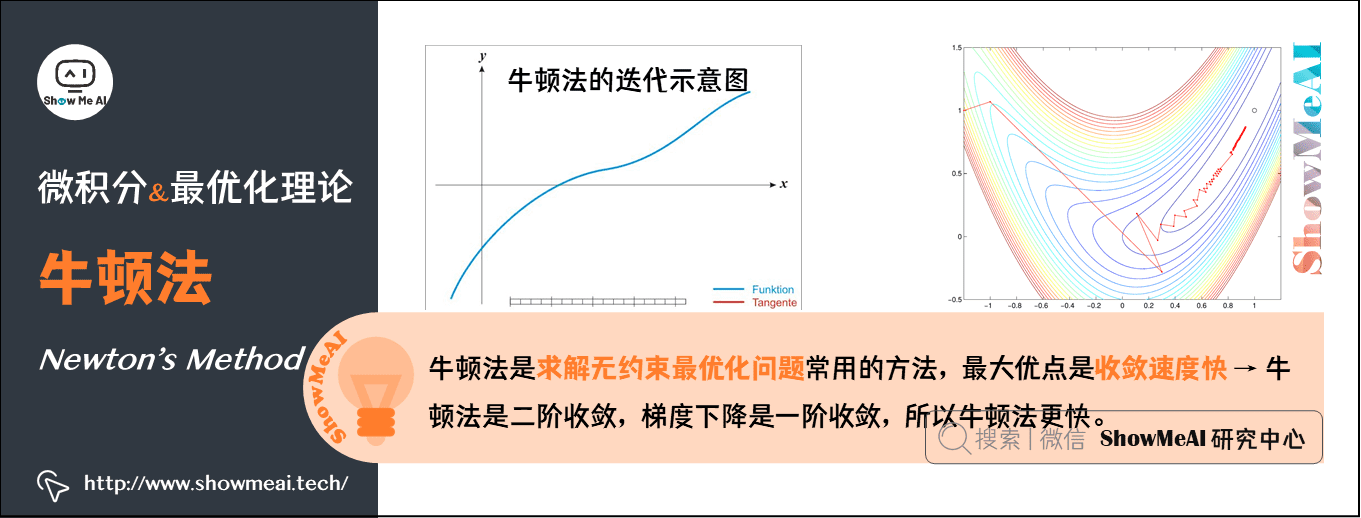
**2.1.1 牛顿-拉夫逊法**

牛顿-拉夫逊法是一种迭代法，用于求解非线性方程。该方法利用函数的一阶导数来构造一个线性近似，并通过迭代更新近似值来逐步逼近方程的根。

function root = newtonRaphson(f, df, x0, tol)
    % 输入：
    % f: 待求解的非线性方程
    % df: f 的一阶导数
    % x0: 初始近似值
    % tol: 容差
    x = x0;
    while abs(f(x)) > tol
        x = x - f(x) / df(x);
    end
    root = x;
end

**逻辑分析：**
牛顿-拉夫逊法从初始近似值 `x0` 开始，通过迭代更新近似值。在每次迭代中，它计算函数 `f` 在当前近似值 `x` 处的导数 `df(x)`，并利用该导数构造一个线性近似。然后，它将近似值更新为 `x - f(x) / df(x)`。该过程重复进行，直到函数值 `f(x)` 的绝对值小于给定的容差 `tol`。

**2.1.2 梯度下降法**

梯度下降法是一种迭代法，用于求解最优化问题。该方法利用函数的梯度来确定下降方向，并通过迭代更新参数值来逐步逼近最优值。

function [x, history] = gradientDescent(f, grad, x0, alpha, tol)
    % 输入：
    % f: 待优化函数
    % grad: f 的梯度
    % x0: 初始参数值
    % alpha: 学习率
    % tol: 容差
    x = x0;
    history = [];
    while norm(grad(x)) > tol
        history = [history, x];
        x = x - alpha * grad(x);
    end
end

**逻辑分析：**
梯度下降法从初始参数值 `x0` 开始，通过迭代更新参数值。在每次迭代中，它计算函数 `f` 在当前参数值 `x` 处的梯度 `grad(x)`，并利用该梯度确定下降方向。然后，它将参数值更新为 `x - alpha * grad(x)`，其中 `alpha` 是学习率。该过程重复进行，直到梯度的范数小于给定的容差 `tol`。

**2.1.3 拟牛顿法**

拟牛顿法是一种迭代法，用于求解非线性优化问题。该方法利用海森矩阵的近似值来构造一个二次近似，并通过迭代更新参数值来逐步逼近最优值。

function [x, history] = quasiNewton(f, grad, H0, x0, tol)
    % 输入：
    % f: 待优化函数
    % grad: f 的梯度
    % H0: 海森矩阵的初始近似值
    % x0: 初始参数值
    % tol: 容差
    x = x0;
    H = H0;
    history = [];
    while norm(grad(x)) > tol
        history = [history, x];
        d = -H \ grad(x);
        x = x + d;
        y = grad(x) - grad(x - d);
        H = H + y * y' / (y' * d) - H * d * d' * H / (d' * H * d);
    end
end

**逻辑分析：**
拟牛顿法从初始参数值 `x0` 和海森矩阵的初始近似值 `H0` 开始，通过迭代更新参数值和海森矩阵的近似值。在每次迭代中，它计算函数 `f` 在当前参数值 `x` 处的梯度 `grad(x)`，并利用该梯度和海森矩阵的近似值 `H` 确定下降方向。然后，它将参数值更新为 `x - H \ grad(x)`。该过程重复进行，直到梯度的范数小于给定的容差 `tol`。

# 3. MATLAB方程求解的实践应用**

**3.1 拟合曲线**

拟合曲线是一种将一组数据点与数学函数相匹配的技术，以便对数据进行