prop.test在R语言中的魔力：统计检验的高效解决方案

# 1. prop.test在R语言中的基础应用

在数据分析领域，进行统计推断是不可或缺的一环。R语言作为统计分析的首选工具之一，提供了强大的统计检验函数。本章节将介绍prop.test在R语言中的基本应用，为读者展示如何在实际数据分析中使用这一工具来检验比例差异。

# 一个简单的prop.test的例子
successes <- c(66, 50) # 成功次数
trials <- c(120, 120) # 总试验次数
prop.test(successes, trials)

这段R代码将会对两个独立样本进行比例检验。prop.test函数通过输入成功次数向量（successes）和试验次数向量（trials），能够计算出两组样本比例差异的统计显著性。

接下来的章节，我们将逐步深入理解prop.test的统计原理和背后的数学模型，以及如何解读其输出结果，进一步在实际案例中应用prop.test，并探索其在大数据环境下的优化与性能调优。

# 2. 深入理解prop.test的统计原理

在探讨prop.test在数据分析中的应用之前，有必要深入理解其背后的统计原理。本章节将逐步揭示prop.test的核心统计概念，理论背景以及参数细节，为高级应用和优化打下坚实的基础。

## 2.1 统计假设检验的概念

### 2.1.1 假设检验的基本步骤

统计假设检验是推断统计的一个核心概念，用于根据样本数据来推断总体参数的特征。prop.test正是这一理论的一个具体应用。检验的基本步骤如下：

1. **提出假设**：包括零假设（H0）和备择假设（H1）。零假设通常表述为“无差异”，而备择假设则表述为“有差异”。
2. **选择检验统计量**：基于数据和假设，选择一个合适的统计量。对于prop.test，通常是样本比例与总体比例差异的标准化Z统计量。
3. **确定显著性水平**：即α值，通常为0.05或0.01，是拒绝零假设的错误概率阈值。
4. **计算检验统计量和P值**：根据样本数据计算检验统计量，并得到P值，即在零假设成立的前提下观测到当前样本或更极端样本的概率。
5. **做出统计决策**：如果P值小于α值，则拒绝零假设，认为有足够的证据支持备择假设；否则，不能拒绝零假设。

### 2.1.2 错误类型及其影响

在假设检验中存在两种类型的错误：

- **第一类错误（α错误）**：错误地拒绝了真实的零假设。
- **第二类错误（β错误）**：错误地没有拒绝错误的零假设。

控制好这两类错误的平衡至关重要，过高的α值可能会导致接受不真实的备择假设（假阳性），而过低的β值则可能无法接受真实的备择假设（假阴性）。通常，α值的选择更受关注，因为它由研究者直接设定。

## 2.2 prop.test的理论背景

### 2.2.1 比例检验的数学模型

prop.test在R语言中主要应用于比例检验，其数学模型基于二项分布。在比例检验中，我们通常检验一个或两个二项比例是否等于某一特定值，或者比较两个比例之间是否有显著差异。

比例检验的数学表达式为：

\[ z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}} \]

其中：
- \( z \)是检验统计量，
- \( \hat{p} \)是样本比例，
- \( p_0 \)是总体比例或假定的比例，
- \( n \)是样本大小。

### 2.2.2 样本比例与总体比例的关系

样本比例是通过观测样本得到的事件发生的频率，而总体比例则是理论上整个总体中事件发生的概率。在prop.test中，我们通常通过样本比例来估计总体比例，或者检验样本比例是否显著地不同于某个假设的总体比例。

如果样本量足够大，根据中心极限定理，样本比例的分布接近正态分布，我们可以利用这一点来进行假设检验。通过prop.test，我们可以对比例进行置信区间估计和假设检验，从而推断总体参数。

## 2.3 prop.test的参数解读

### 2.3.1 主要参数与选项的解释

在R语言中，prop.test函数有若干参数，通过这些参数可以实现不同的检验类型。prop.test函数的基本形式如下：

prop.test(x, n, p = NULL, alternative = c("two.sided", "less", "greater"), 
          conf.level = 0.95, correct = TRUE)

其中：
- **x**：在单比例检验中，是事件发生的频数；在双比例检验中，是两个二项样本中事件发生次数的向量。
- **n**：与x对应的样本大小向量。
- **p**：在单比例检验中，是期望总体比例的值。
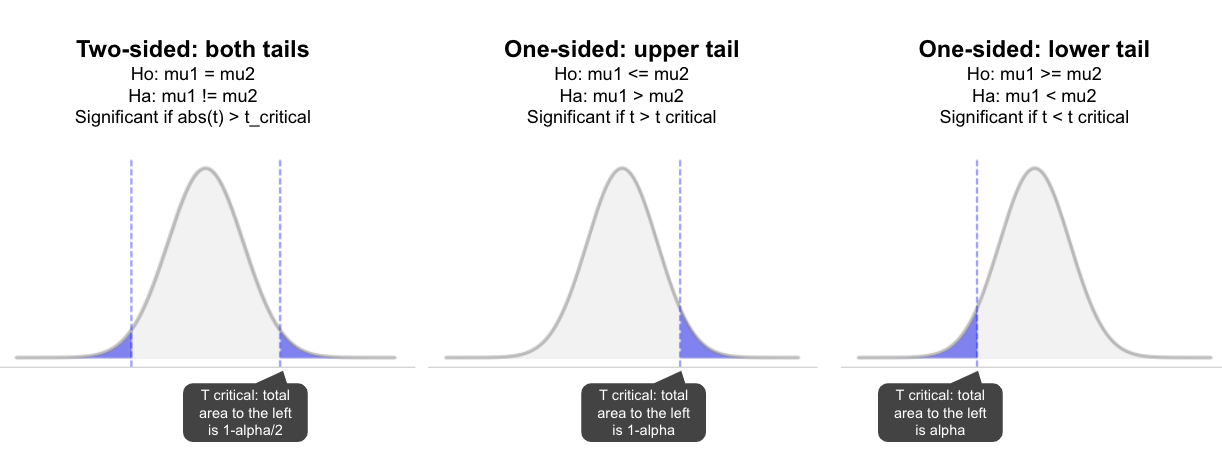
- **alternative**：指定备择假设的类型，可以是双侧检验("two.sided")，左侧检验("less")或右侧检验("greater")。
- **conf.level**：置信水平，默认为95%。
- **correct**：是否应用连续性校正，通常在小样本情况下使用。

### 2.3.2 参数的默认值与调整

prop.test的参数默认值都是经过深思熟虑设置的，以适应大多数情况。例如，默认的置信水平为95%，这是统计学中常用的标准。连续性校正（Yates校正）默认开启，以减少在小样本情况下对二项分布离散性的估计误差。

然而，根据不同的需求和数据特性，研究者可能需要调整这些参数。如在处理大样本数据时，可以关闭连续性校正，而在需要更严格的显著性测试时，可以提高置信水平。

# 使用prop.test进行单比例检验的示例代码
prop.test(x = 25, n = 100, p = 0.25, conf.level = 0.99)

在上述示例中，我们对一个样本比例进行了单侧检验，设置了一个更高（99%）的置信水平，并假设总体比例为0.25。这个例子演示了如何通过参数调整来达到特定的统计目的。

接下来，我们将进入第三章，探索prop.test在数据分析中的实践技巧，以及如何应用这些统计原理在现实世界的数据分析中。

# 3. prop.test在数据分析中的实践技巧

在第三章中，我们将深入探讨`prop.test`在数据分析中的实际应用，包括单比例检验、双比例检验，以及在更复杂场景下的高级应用。通过实际案例分析和应用技巧的展示，我们将揭示`prop.test`如何在处理真实世界数据时发挥其强大的统计检验功能。

## 3.1 单比例检验的案例分析

### 3.1.1 使用`prop.test`进行单比例检验的步骤

单比例检验是最基本的统计检验之一，常用于检验样本中的某事件发生比例是否与假设的总体比例相等。在R语言中，`prop.test`函数可以轻松实现这一检验。以下是进行单比例检验的基本步骤：

1. **数据准备**：确定样本数据和预期比例。
2. **应用`prop.test`**：输入样本比例、样本大小，以及预期比例。
3. **解读结果**：理解输出的检验统计量和p值。

下面是一个单比例检验的R代码示例：

# 假设有一个样本，其中有60次事件发生，样本总数为200。
sample.prop <- 60 / 200
expected.prop <- 0.3  # 假设的总体比例为0.3

# 使用prop.test进行单比例检验
test.result <- prop.test(x = sample.prop, n = 200, p = expected.prop)

print(test.result)

### 3.1.2 结果解读与报告撰写

在得到`prop.test`输出后，关键步骤是解读这些结果，并撰写分析报告。输出将包括以下内容：

- **估计比例**：样本中的事件发生比例。
- **置信区间**：事件发生比例的置信区间，可以帮助我们了解样本比例与总体比例的差距。
- **统计检验量**：例如z值，用以衡量样本比例与预期比例之间的差异是否具有统计学意义。
- **p值**：用于判断结果的统计显著性。通常如果p值小于0.05，我们拒绝原假设，认为样本比例与预期比例不同。

报告中应当清晰地说明检验的假设、使用的样本数据、统计显著性结果，以及对于总体比例可能产生的实际意义。此外，报告中可能还需要讨论结果的局限性和假设条件。

## 3.2 双比例检验的应用场景

### 3.2.1 双比例检验的基本步骤

双比例检验用于比较两个独立样本中事件发生比例的差异。例如，在A组和B组的医学研究中，我们可能想要知道两组的治疗效果是否存在显著差异。以下是双比例检验的基本步骤：

1. **确定两组样本数据**：分别计算A组和B组的事件发生比例。
2. **应用`prop.test`**：使用两组样本数据进行检验。
3. **结果解读**：分析两组比例是否存在统计学差异。

这里是一个双比例检验的R代码示例：

# 假设A组有30次事件发生，样本总数为100。
# B组有20次事件发生，样本总数为120。
sampleA <- 30
totalA <- 100
sampleB <- 20
totalB <- 120

# 使用prop.test进行双比例检验
test.result <- prop.test(x = c(sampleA, sampleB), n = c(totalA, totalB))

print(test.result)

### 3.2.2 实例演示与结果分析

在执行了双比例检验之后，接下来是将检验结果转化为实际的业务或科研决策。输出结果通常包括：

- **z值**和**p值**：用于判断两组样本比例是否存在统计