揭示MATLAB矩阵内部结构：深入分析，掌握底层原理

# 1. MATLAB矩阵基础

MATLAB矩阵是MATLAB中用于存储和操作数据的核心数据结构。它是一个二维数组，其元素可以是任何数据类型，包括数字、字符串和逻辑值。

矩阵在MATLAB中使用方括号表示，元素用逗号分隔。例如，以下代码创建了一个3x3矩阵：

A = [1, 2, 3; 4, 5, 6; 7, 8, 9]

矩阵可以具有任意大小，并且可以进行各种操作，包括加法、减法、乘法和除法。MATLAB还提供了许多内置函数来处理矩阵，例如求逆、求特征值和求奇异值分解。

# 2. MATLAB矩阵的内部结构

### 2.1 矩阵存储格式

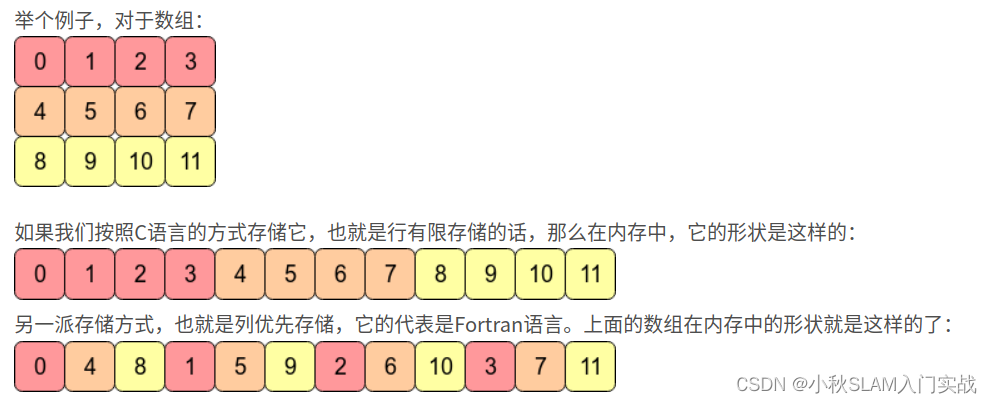
MATLAB矩阵采用列优先顺序存储在内存中。这意味着矩阵中的元素按列存储，而不是按行存储。例如，以下3x3矩阵：

A = [1 2 3; 4 5 6; 7 8 9]

将存储为以下线性数组：

[1 4 7 2 5 8 3 6 9]

列优先顺序存储格式的优点是，它可以提高矩阵操作的效率，例如矩阵乘法和求逆。

### 2.2 矩阵稀疏性

稀疏矩阵是包含大量零元素的矩阵。MATLAB提供稀疏矩阵数据类型，称为`sparse`，用于有效存储和操作稀疏矩阵。稀疏矩阵存储为三个数组：

- 值数组：存储非零元素的值
- 行索引数组：存储非零元素的行索引
- 列索引数组：存储非零元素的列索引

例如，以下稀疏矩阵：

A = [1 0 3; 0 5 0; 7 0 9]

将存储为以下三个数组：

vals = [1 3 5 7 9]
rows = [1 1 2 3 3]
cols = [1 3 2 1 3]

稀疏矩阵的优点是，它可以显着节省内存和计算时间，尤其是在处理大型稀疏矩阵时。

### 2.3 矩阵块结构

MATLAB允许将矩阵划分为更小的块。这对于处理大型矩阵或对矩阵的特定部分进行操作非常有用。要创建矩阵块，可以使用`blkdiag`函数。例如，以下代码创建两个2x2矩阵的块对角线矩阵：

A = [1 2; 3 4];
B = [5 6; 7 8];
C = blkdiag(A, B);

`C`现在是一个4x4矩阵，其中`A`和`B`作为对角线块：

C = [1 2 0 0; 3 4 0 0; 0 0 5 6; 0 0 7 8]

矩阵块结构的优点是，它可以简化对矩阵特定部分的操作，并提高大型矩阵的内存管理效率。

# 3. MATLAB矩阵操作的底层原理

### 3.1 矩阵加法和减法

矩阵加法和减法是MATLAB中两个最基本的矩阵操作。它们通过逐元素的方式进行，这意味着两个矩阵中对应元素相加或相减。

A = [1 2 3; 4 5 6; 7 8 9];
B = [10 11 12; 13 14 15; 16 17 18];

C = A + B; % 矩阵加法
D = A - B; % 矩阵减法

**代码逻辑分析：**

* `A + B` 将矩阵 `A` 和 `B` 中对应元素相加，得到矩阵 `C`。
* `A - B` 将矩阵 `A` 和 `B` 中对应元素相减，得到矩阵 `D`。

**参数说明：**

* `A` 和 `B`：参与加法或减法的两个矩阵。
* `C` 和 `D`：加法或减法的结果矩阵。

### 3.2 矩阵乘法

矩阵乘法是MATLAB中另一个重要的矩阵操作。它通过将第一个矩阵的行向量与第二个矩阵的列向量逐元素相乘并求和来计算。

A = [1 2 3; 4 5 6; 7 8 9];
B = [10 11 12; 13 14 15; 16 17 18];

C = A * B; % 矩阵乘法

**代码逻辑分析：**

* `A * B` 将矩阵 `A` 的行向量与矩阵 `B` 的列向量逐元素相乘并求和，得到矩阵 `C`。

**参数说明：**

* `A` 和 `B`：参与乘法的两个矩阵。
* `C`：乘法的结果矩阵。

### 3.3 矩阵求逆

矩阵求逆是MATLAB中一个高级的矩阵操作。它通过求解线性方程组来计算矩阵的逆矩阵。

A = [1 2 3; 4 5 6; 7