共轭转置在MATLAB信号处理中的应用：深入理解信号处理的奥秘

# 1. 共轭转置的概念和数学基础

共轭转置是线性代数中一个重要的概念，在信号处理等领域有着广泛的应用。它表示一个矩阵或向量的元素按行和列互换后的新矩阵或向量。

**定义：**
给定一个复数矩阵或向量 A，其共轭转置记为 A^H，定义为：

A^H = A^* = (A^*)^T

其中，A^* 表示 A 的共轭，T 表示 A 的转置。

**性质：**
共轭转置具有以下性质：
* (A^H)^H = A
* (AB)^H = B^H A^H
* (A + B)^H = A^H + B^H
* (cA)^H = c*A^H，其中 c 是一个复数

# 2. 共轭转置在信号处理中的应用

### 2.1 信号的共轭转置

#### 2.1.1 共轭转置的定义和性质

共轭转置，也称为埃尔米特转置，是线性代数中的一种运算。对于一个复数矩阵 A，其共轭转置 A* 定义为：

A* = A^H = (A^T)^*

其中：

* A^T 表示 A 的转置矩阵
* ^* 表示共轭运算

共轭转置具有以下性质：

* **共轭对称性：** (A*)* = A
* **线性性：** (aA + bB)* = aA* + bB*
* **乘法分配律：** (AB)* = B*A*
* **逆矩阵：** (A*)^-1 = (A^-1)*
* **行列式：** det(A*) = det(A)^*

#### 2.1.2 共轭转置在信号处理中的意义

在信号处理中，共轭转置用于处理复数信号。复数信号由实部和虚部组成，共轭转置可以将复数信号的虚部取反。

对于一个复数信号 x(n)，其共轭转置 x*(n) 定义为：

x*(n) = x(n)^*

其中：

* x(n) 是实部和虚部分别为 Re(x(n)) 和 Im(x(n)) 的复数信号
* x*(n) 是实部为 Re(x(n))，虚部为 -Im(x(n)) 的复数信号

### 2.2 共轭转置在滤波中的应用

#### 2.2.1 滤波器设计的概念

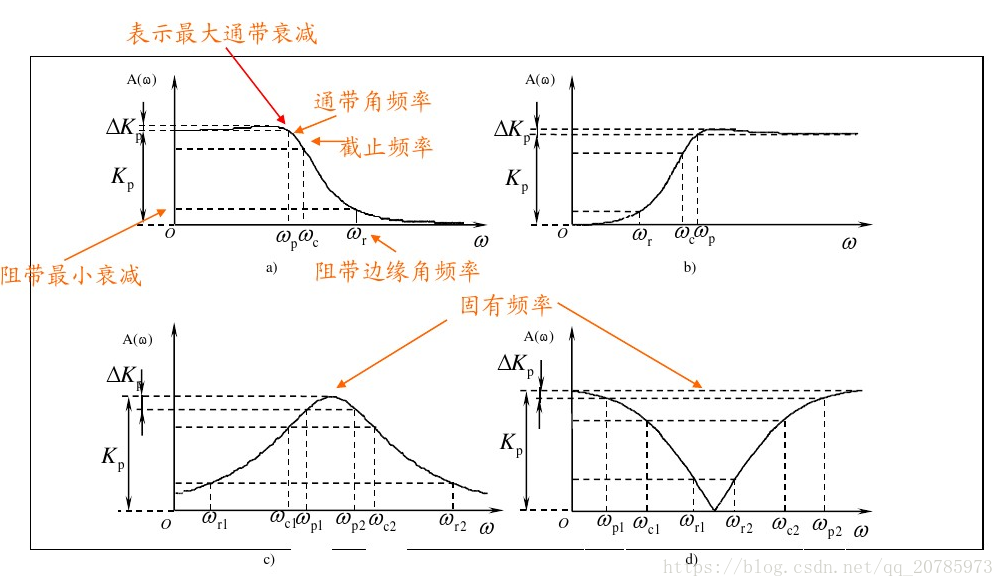
滤波器是一种处理信号的设备或算法，用于滤除信号中的特定频率分量。滤波器设计是确定滤波器的特性，如通带、阻带和截止频率的过程。

#### 2.2.2 共轭转置在滤波器设计中的作用

共轭转置在滤波器设计中用于设计滤波器的传递函数。传递函数是滤波器输出信号与输入信号的比率。

对于一个复数滤波器，其传递函数 H(ω) 定义为：

H(ω) = |H(ω)|e^(jθ(ω))

其中：

* |H(ω)| 是幅度响应
* θ(ω) 是相位响应

共轭转置可以用来设计滤波器的幅度响应和相位响应。通过对传递函数取共轭转置，可以得到滤波器的共轭传递函数 H*(ω)，其幅度响应不