控制系统的数学工具】：对角线标准型计算技巧，精确控制的秘诀


# 摘要
本文系统地介绍了控制系统中数学工具的基础知识，深入讲解了对角线标准型的理论、计算方法及其在控制系统中的应用。通过对角线标准型的稳定性分析和数学定义，文章阐述了其在设计简单控制策略、系统解耦与性能优化方面的重要性。随后，文章探讨了精确控制系统构建过程中的需求、挑战与数学模型，并详细讨论了精确控制算法的设计与实现。在实践部分，文章通过多个实例分析了对角线标准型的计算技巧及其在电机控制、多变量系统、动态系统调试中的应用。最后，文章展望了对角线标准型在非线性系统、复杂控制系统中的扩展应用以及智能控制领域的未来发展趋势。

# 关键字
控制系统；数学工具；对角线标准型；稳定性分析；精确控制；系统解耦

参考资源链接：[状态方程对角线标准型转换详解：控制系统状态空间关键步骤](https://wenku.csdn.net/doc/4dmnejuv3j?spm=1055.2635.3001.10343)
# 1. 控制系统数学工具基础

控制系统是现代工程的基石，而数学工具则是理解和设计这些系统的基础。本章将介绍控制系统中常用的数学工具，并为后续章节中对角线标准型的深入探讨打下基础。

## 1.1 控制系统的基本组成

控制系统由多个部分组成，包括输入、输出、过程（或系统）和反馈环节。控制系统的目标是通过调整输入信号，使得输出信号达到预期的状态。为了实现这一目标，控制系统中采用了一系列的数学工具，包括微积分、线性代数、微分方程等。

## 1.2 线性代数在控制系统中的作用

线性代数是研究向量空间及其线性变换的数学分支，在控制系统设计中扮演着关键角色。它用于描述和解决多变量系统的问题，尤其是状态空间表示法，它将系统行为描述为向量空间中的线性变换，使得系统分析变得更为直观。

## 1.3 拉普拉斯变换与传递函数

拉普拉斯变换是控制系统分析中的另一个重要工具，它将时间域内的微分方程转换为复频域内的代数方程。通过拉普拉斯变换，复杂的时间响应问题可以转化为更加简单的代数问题。传递函数作为拉普拉斯变换的一个结果，描述了系统输入和输出之间的数学关系，是控制系统分析和设计的核心。

通过本章的学习，读者将掌握控制系统中基础数学工具的应用，并为深入理解后续章节中对角线标准型理论与实践案例奠定坚实的基础。

# 2. 对角线标准型理论详解

### 2.1 对角线标准型的定义与性质

#### 线性系统的稳定性分析

在控制系统领域，对角线标准型是线性系统分析和设计中的一个重要概念。它为系统稳定性分析和控制策略设计提供了一种简化的模型。系统稳定性是任何控制系统设计的首要考量因素。一个控制系统是稳定的，如果它的所有状态变量随时间趋向于零。稳定性分析通常涉及系统的特征值，这些特征值决定了系统状态的动态行为。

在对角线标准型中，一个线性系统的矩阵表示可以通过相似变换转换为对角矩阵形式，其对角元素即为系统的特征值。系统稳定性可以通过分析这些特征值来进行。一般而言，如果一个系统的特征值都具有负的实部，则系统是稳定的。反之，如果至少有一个特征值具有正的实部，则系统不稳定。

#### 对角线标准型的数学定义

对角线标准型是数学上的一种特殊形式，特别适用于线性代数中的矩阵理论。对于一个给定的线性系统，假设其状态空间表达式为：

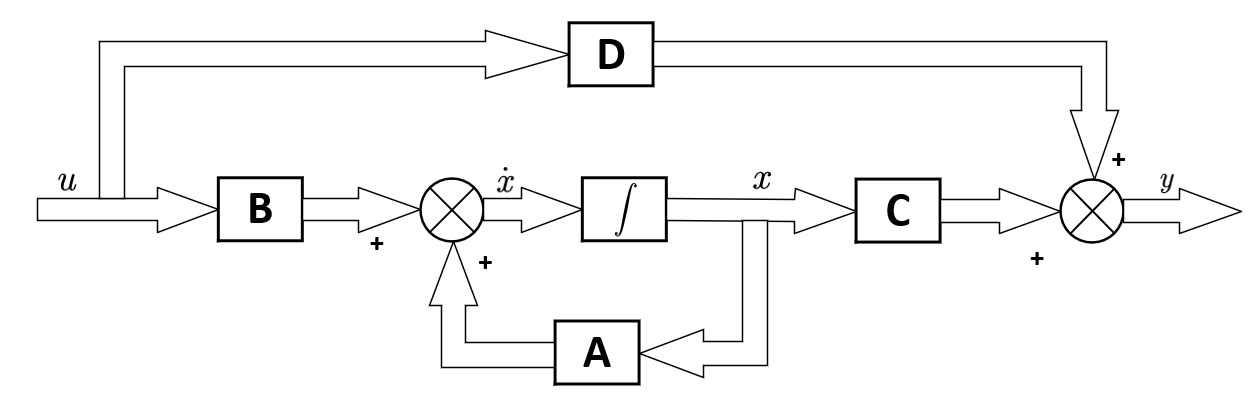
\[ \dot{x}(t) = Ax(t) + Bu(t) \]
\[ y(t) = Cx(t) + Du(t) \]

其中，\(A\) 是系统的状态矩阵，\(x(t)\) 是状态向量，\(u(t)\) 是输入向量，\(y(t)\) 是输出向量，\(B\)、\(C\) 和 \(D\) 分别是输入、输出和直接传递矩阵。对角线标准型将状态矩阵 \(A\) 通过相似变换转换为一个对角矩阵 \(A_d\)。

对角线标准型的数学定义可以形式化为：

\[ A_d = T^{-1}AT \]

在这里，\(T\) 是一个非奇异矩阵，通过适当的变换，将状态矩阵 \(A\) 转换为对角矩阵 \(A_d\)。对角线上的元素为系统的特征值。

### 2.2 对角线标准型的计算方法

#### 状态空间表达式与特征值

为了计算一个给定线性系统的对角线标准型，首先需要确立系统的状态空间表达式。在状态空间模型中，系统的动态行为可以通过矩阵 \(A\)、\(B\)、\(C\) 和 \(D\) 来描述。特征值分析是对角化过程中的核心步骤，因为对角线上的元素正是系统矩阵 \(A\) 的特征值。

计算特征值的数学方法包括求解特征方程：

\[ \det(A - \lambda I) = 0 \]

其中，\(I\) 是单位矩阵，\(\lambda\) 表示矩阵 \(A\) 的特征值。求解这个方程可以得到系统的特征值，这些值是确定系统行为的关键。

#### 对角化变换的过程

对角化是一个数学变换过程，它将状态矩阵 \(A\) 转换为对角矩阵 \(A_d\)。这一过程涉及到找到一个非奇异矩阵 \(T\)，使得：

\[ A_d = T^{-1}AT \]

当矩阵 \(A\) 可以被对角化时，存在一个由 \(A\) 的特征向量组成的矩阵 \(T\)，并且 \(A\) 的特征值将构成对角矩阵 \(A_d\) 的对角元素。在实际操作中，求解 \(T\) 和 \(A_d\) 涉及到计算 \(A\) 的特征向量和特征值，并确保 \(T\) 由线性独立的特征向量构成。

对角化过程的计算通常借助数学软件工具完成，如MATLAB。在MATLAB中，可以使用 `eig(A)` 函数来求解矩阵 \(A\) 的特征值和特征向量，然后通过构造矩阵 \(T\) 来计算对角矩阵 \(A_d\)。

### 2.3 对角线标准型在控制系统中的应用

#### 设计简单控制策略

对角线标准型简化了控制系统的分析和设计过程，特别是当系统具有多个输入和输出时。在这种标准型下，每个状态变量仅由一个输入单独控制，从而允许工程师设计更为简单的控制策略。

对于设计简单的控制策略，首先需要将系统的状态矩阵对角化。接下来，针对每个对角元素（即特征值），可以设计独立的反馈回路。因为对角化后的系统是解耦的，每个状态变量的动态行为可以单独考虑，从而简化了控制器的设计。

例如，在多变量控制系统中，可以针对每个对角线上的状态变量设计一个简单的比例-积分-微分（PID）控制器，独立地调整系统的性能。

#### 系统解耦与性能优化

对角线标准型的另一个重要应用是实现系统的解耦和性能优化。在控制系统的动态分析中，解耦意味着系统的各个子系统之间没有相互作用，因此可以独立控制。性能优化则关注于提高系统的响应速度、稳定性以及抗干扰能力等。

在对角线标准型中，由于状态矩阵已经被简化为对角矩阵，系统的各个状态变量可以被看作是独立的，这样可以分别设计控制器来调节每个变量，以达到解耦的目的。通过这种解耦，可以减少控制过程中的耦合效应，从而使整个系统的性能得到改善。

例如，对于一个具有多输入多输出（MIMO）特性的控制系统，可以使用对角线标准型来实现各个控制通道的解耦，然后使用适当的控制器设计方法，如LQR（线性二次调节器），来优化整个系统的性能。

总结而言，对角线标准型为控制系统的设计和分析提供了一种强有力的工具。它通过简化系统模型，使得工程师能够更有效地分析系统行为，并设计出更为高效和可靠的控制策略。在下一章节中，我们将更深入地探讨对角线标准型在不同控制系统的应用实例，包括电机控制系统和多变量系统的对角化过程和应用。

# 3. 精确控制系统的构建与分析

## 3.1 精确控制的需求与挑战
### 3.1.1 系统误差与控制精度的关系
精确控制系统的核心目标是实现高精度的控制。系统误差是指控制系统输出与期望输出之间的差异。控制精度则直接与系统误差的最小化密切相关。对于任何控制系统而言，减少系统误差并提高控制精度始终是最紧迫的需求之一。为了达到这一目标，系统设计者需要采用一系列的方法和措施来减少各种误差源的影响，包括测量误差、模型误差、参数误差等。例如，通过改进传感器技术、使用高级的控制算法、进行细致的系统辨识和参数估计来提高控制精度。

### 3.1.2 实时反馈与控制调整机制
为了实现精确控制，实时反馈机制至关重要。实时反馈允许系统动态地调整控制输入，以响应环境变化和系统内部动态。控制调整机制的实现依赖于精确的传感器来测量关键参数，然后通过反馈回路将这些参数与控制目标进行比较，从而调整控制指令。例如，在温度控制系统中，温度传感器不断监测环境温度，并将信息反馈给控制器。控制器随即分析这些数据，并根据预先设定的控制算法来调整加热或冷却装置的输出，以维持目标温度。

## 3.2 精确控制系统的数学模型建立
### 3.2.1 输入输出模型与传递函数