【多元方差分析案例】：car包在MANOVA中的实际应用揭秘

# 1. 多元方差分析（MANOVA）概述

多元方差分析（MANOVA）是统计学中一种用于检验两个或多个分组间多个因变量是否存在显著差异的方法。本章将带您了解MANOVA的基本概念、它的应用背景，以及为什么在处理多变量问题时比单变量方差分析（ANOVA）更具有优势。MANOVA不仅能告诉我们组间是否有差异，还能揭示差异在哪些变量组合上最为显著，这在多变量数据分析中具有重大意义。

## 1.1 MANOVA的定义与用途
多元方差分析是对多因变量数据集进行统计检验的一种方法，旨在检查两组或多组之间的均值向量是否存在显著差异。MANOVA允许我们同时考虑多个响应变量，从而对组间的整体差异进行综合评估，这对于研究复杂的交互效应和协同变化尤为有用。

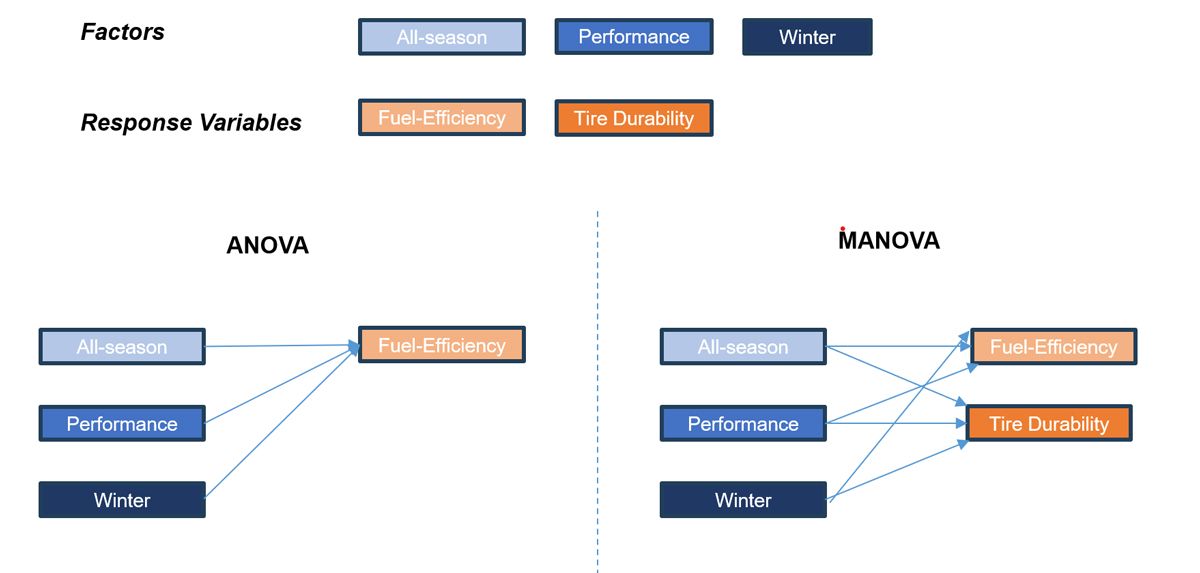
## 1.2 MANOVA与ANOVA的对比
MANOVA可以看作是ANOVA的扩展，它在多个响应变量的条件下进行。与单变量ANOVA相比，MANOVA在处理多响应数据时有两大优势：首先，MANOVA减少了因多次测试导致的I型错误率上升的风险；其次，通过多变量分析可以揭示变量间的复杂关系，如变量之间的相关性如何影响组间差异。

## 1.3 MANOVA的应用场景
在诸如心理测量、医学试验、市场研究等领域，研究者常会收集多个相关的定量变量。MANOVA可以帮助研究者在考虑多个反应变量的同时检验组间差异，从而在统计上提供更丰富的信息。在教育领域，它可以用来评估不同的教学方法对学生成绩多方面的影响；在医疗研究中，可以用来观察不同治疗方法对患者多个健康指标的影响。

通过本章的概述，您将对MANOVA有一个初步的认识，并了解到它在多变量数据分析中的应用价值。接下来的章节将通过具体的实践步骤，使用R语言中car包进行数据处理和MANOVA分析。

# 2. 使用R语言中的car包准备数据

## 2.1 数据的收集与整理

### 2.1.1 数据获取方法

在数据分析和统计研究中，数据的获取是一个非常重要的步骤。R语言提供了多种方式来获取数据，包括但不限于：

- **直接输入**：对于小型数据集，可以直接在R中创建数据框（data frame）。
- **从文件导入**：R语言支持导入多种格式的数据文件，如CSV、Excel、文本文件等。
- **数据库连接**：使用R的数据库接口包（如`DBI`和`RODBC`），可以直接从数据库中查询数据。
- **在线API**：通过R的`httr`或`RCurl`包，可以从网络API获取数据。
- **爬虫技术**：使用`rvest`或`httr`包编写爬虫，从网页中抓取数据。

在使用R语言获取数据时，需要注意数据的格式和结构，确保数据的整洁性和一致性。例如，当从CSV文件导入数据时，可以使用`read.csv()`函数，并可以指定数据分隔符、缺失值符号等参数。

# 示例：从CSV文件读取数据
data <- read.csv("path/to/your/data.csv", header = TRUE, sep = ",", na.strings = c("NA", "", " "))

### 2.1.2 数据预处理技巧

数据预处理是数据分析前的关键步骤，涉及数据清洗、转换和规范化等。以下是一些常见的数据预处理技巧：

- **缺失值处理**：可以使用多种方法处理缺失值，如删除含有缺失值的记录、填充缺失值（如平均值、中位数填充等）。
- **数据标准化**：数据标准化（如z-score标准化）是为了消除不同量纲的影响。
- **转换分类变量**：将非数值型数据转换为数值型数据，例如使用`factor()`函数转换因子变量。
- **数据筛选**：根据特定条件筛选出所需的数据子集。
- **数据合并**：在有多个数据源时，可能需要合并数据，使用`merge()`函数或`dplyr`包中的`left_join()`等函数。

# 示例：数据标准化
data$normalized_column <- (data$column - mean(data$column, na.rm = TRUE)) / sd(data$column, na.rm = TRUE)

# 示例：转换分类变量
data$category_column <- factor(data$category_column)

## 2.2 car包的基本使用

### 2.2.1 car包功能简介

`car`包（Companion to Applied Regression）是R中一个非常强大的包，它提供了许多方便的函数来辅助线性和广义线性模型的分析。`car`包的主要功能包括但不限于：

- 提供稳健的线性模型估计。
- 支持交互作用图的绘制。
- 实现方差分析（ANOVA）和多元方差分析（MANOVA）。
- 管理虚拟变量。
- 提供条件诊断图。
- 计算多重比较和其他多重测试。

安装`car`包可以使用`install.packages("car")`命令，之后通过`library(car)`命令加载包。

### 2.2.2 数据探索性分析

在进行任何深入的统计分析之前，进行探索性数据分析（Exploratory Data Analysis，EDA）是非常重要的。这可以帮助理解数据的基本结构和特征，并且揭示可能存在的问题。`car`包提供了一些非常有用的函数来进行EDA，例如：

- `leveneTest()`：用于检验方差齐性。
- `qqPlot()`：绘制分位数-分位数图来检验数据的正态性。
- `scatterplotMatrix()`：绘制变量之间的散点图矩阵，有助于观察变量间的关系。

# 示例：方差齐性检验
library(car)
leveneTest(your_data$dependent_variable ~ your_data$independent_variable, data = your_data)

# 示例：正态性检验
qqPlot(your_data$dependent_variable)

## 2.3 多元数据的描述性统计

### 2.3.1 均值向量和协方差矩阵

在准备多元数据进行分析时，描述性统计是首要步骤。