MATLAB指数函数与仿真建模:构建虚拟环境,探索复杂系统
发布时间: 2024-06-09 20:55:35 阅读量: 93 订阅数: 58 


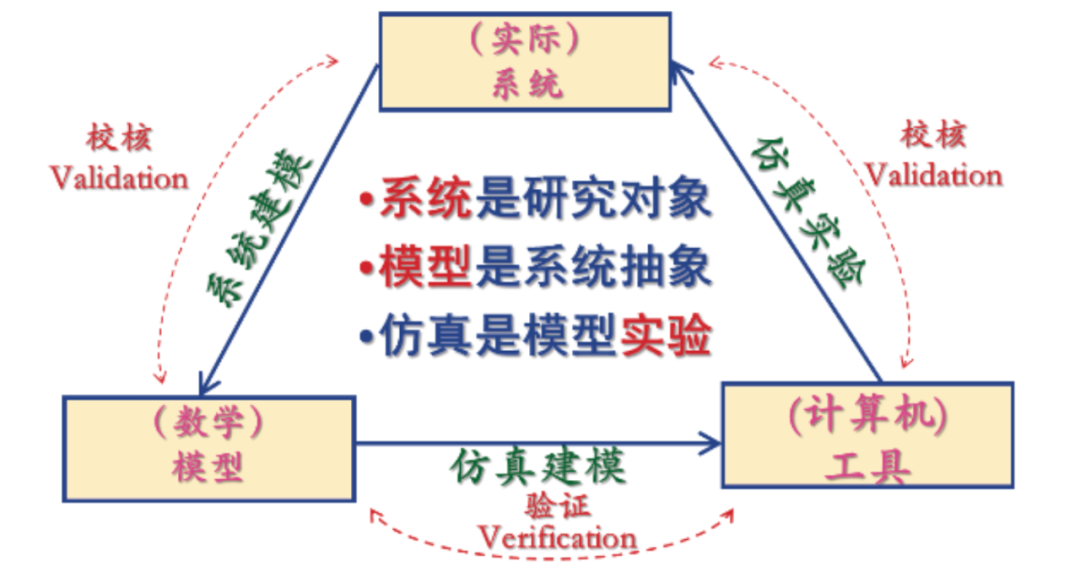
MATLAB的仿真应用
# 1. MATLAB指数函数的数学基础
指数函数在数学和工程领域中有着广泛的应用,在MATLAB中,指数函数是一个重要的数学工具,用于建模各种现象。本节将介绍指数函数的数学基础,包括其定义、性质和导数。
**定义**:指数函数以 e 为底的幂函数,表示为 f(x) = e^x,其中 e 是自然对数的底,约为 2.71828。
**性质**:
- **单调性**:指数函数在整个实数范围内单调递增。
- **凸性**:指数函数在整个实数范围内凸向上。
- **极限**:当 x 趋于正无穷时,e^x 趋于正无穷;当 x 趋于负无穷时,e^x 趋于 0。
# 2. MATLAB指数函数的编程实现
### 2.1 指数函数的语法和参数
MATLAB中的指数函数`exp`用于计算自然指数函数,即`e^x`。其语法为:
```
y = exp(x)
```
其中:
* `x`:输入值,可以是标量、向量或矩阵。
* `y`:输出值,与`x`具有相同的大小和类型。
### 2.2 指数函数的数值计算
`exp`函数使用数值方法来计算指数值。默认情况下,它使用基于泰勒级数展开的算法。对于大多数实际应用,该算法提供了足够的精度。
**代码块:**
```
% 计算自然指数函数
x = linspace(-5, 5, 100);
y = exp(x);
% 绘制指数函数的图像
plot(x, y, 'b-', 'LineWidth', 2);
xlabel('x');
ylabel('exp(x)');
title('指数函数的数值计算');
grid on;
```
**逻辑分析:**
* `linspace`函数生成一个从-5到5的100个均匀间隔点的向量。
* `exp`函数计算每个点的自然指数值。
* `plot`函数绘制指数函数的图像。
* `xlabel`、`ylabel`和`title`函数设置轴标签和标题。
* `grid on`函数显示网格线。
### 2.3 指数函数的图形化表示
`exp`函数可以用于绘制指数函数的图形。指数函数的图像是一个单调递增的曲线,其形状取决于输入值。
**代码块:**
```
% 定义指数函数
f = @(x) exp(x);
% 绘制指数函数的图像
fplot(f, [-5, 5]);
xlabel('x');
ylabel('exp(x)');
title('指数函数的图形化表示');
grid on;
```
**逻辑分析:**
* `fplot`函数绘制指定函数的图像。
* `xlabel`、`ylabel`和`title`函数设置轴标签和标题。
* `grid on`函数显示网格线。
# 3. 指数函数在仿真建模中的应用
指数函数在仿真建模中具有广泛的应用,它可以用来模拟各种自然现象和工程系统中的增长、衰减、振荡和波浪等行为。
### 3.1 增长和衰减模型
指数函数最常见的应用之一是模拟增长和衰减过程。
#### 3.1.1 人口增长模型
人口增长模型使用指数函数来模拟人口数量随时间的变化。该模型假设人口增长率与人口数量成正比,即:
```matlab
% 人口增长模型
function population_growth(r, P0, t)
% r: 增长率
% P0: 初始人口数量
% t: 时间
% 计算人口数量
P = P0 * exp(r * t);
% 输出结果
disp(['时间:' num2str(t) ' 年,人口数量:' num2str(P)]);
end
```
**代码逻辑分析:**
* `exp(r * t)` 计算人口数量随时间的指数增长。
* `disp()` 输出人口数量结果。
**参数说明:**
* `r`: 增长率,正值表示增长,负值表示衰减。
* `P0`: 初始人口数量。
* `t`: 时间,单位为年。
#### 3.1.2 放射性衰变模型
放射性衰变模型使用指数函数来模拟放射性元素的衰变过程。该模型假设放射性元素的衰变率与元素数量成正比,即:
```matlab
% 放射性衰变模型
function radioactive_decay(lambda, N0, t)
% lambda: 衰变率
% N0: 初始元素数量
% t: 时间
% 计算元素数量
N = N0 * exp(-lambda * t);
% 输出结果
disp(['时间:' num2str(t) ' 年,元素数量:' num2str(N)]);
end
```
**代码逻辑分析:**
* `exp(-lambda * t)` 计算元素数量随时间的指数衰减。
* `disp()` 输出元素数量结果。
**参数说明:**
* `lambda`: 衰变率,正值表示衰变。
* `N0`: 初始元素数量。
* `t`: 时间,单位为年。
### 3.2 振荡和波浪模型
指数函数还可以用来模拟振荡和波浪等周期性行为。
#### 3.2.1 正弦波模型
正弦波模型使用指数函数来模拟正弦波的振荡。该模型的方程为:
```
y = A * sin(2 * pi * f * t + phi)
```
其中:
* `y`: 振幅。
* `A`: 幅度。
* `f`: 频率。
* `t`: 时间。
* `phi`: 相位角。
0
0





