【DS18B20温度数据深度分析】：算法处理与分析的高级技术


# 摘要
DS18B20传感器在温度数据采集和分析中发挥关键作用，本文首先概述了DS18B20传感器及其数据采集方法，然后深入探讨了温度数据的基础算法处理，包括数字信号的滤波、数据平滑处理及异常值检测与处理。接着，文章转向高级温度数据分析技术，如趋势分析、统计学应用和机器学习技术的运用，以及这些方法在工业、农业和室内环境监测中的实际应用案例。最后，本文介绍了DS18B20数据分析工具与平台，并探讨了未来传感器技术、大数据和人工智能的融合趋势，以及这些技术进步如何影响温度数据的处理和应用。

# 关键字
DS18B20传感器；数据采集；滤波算法；异常值处理；趋势分析；机器学习；大数据；人工智能；物联网技术；环境监测

参考资源链接：[DS18B20序列号读取与LCD显示实现](https://wenku.csdn.net/doc/5guib0xxma?spm=1055.2635.3001.10343)
# 1. DS18B20传感器概述与数据采集

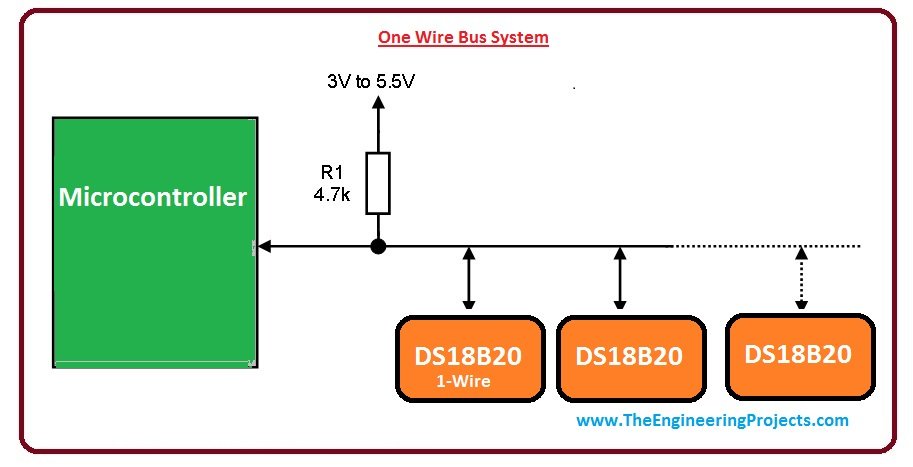
DS18B20是单总线数字温度传感器，广泛应用于各种环境温度检测领域。该传感器以其精确度高、稳定性好、功耗低等优点，成为了温度检测的首选。DS18B20能够输出9位至12位的摄氏温度值，并且具有可编程报警功能。

## 数据采集基础

采集DS18B20数据时，关键步骤包括初始化传感器、发送温度转换命令、等待转换完成，以及读取温度数据。以下为采集DS18B20温度数据的基础步骤：

1. 初始化DS18B20：通过单总线发送重置脉冲，让传感器准备进行数据通信。
2. 发送温度转换命令：通常是发送“Convert T”命令，让DS18B20开始测量温度。
3. 等待转换完成：DS18B20将温度值转换为数字信号，这一过程需要一定的时间。
4. 读取温度数据：最后通过单总线从DS18B20读取温度值。

// 示例：DS18B20基本读取函数
void readTemperature() {
    // 初始化总线
    OneWire_reset(&bus);
    // 发送温度转换命令
    OneWire_writeByte(&bus, 0x44);
    // 等待转换完成（这里可以使用延时或中断）
    delay(750); // 等待大约750ms
    // 读取温度数据
    int16_t temp = OneWire_readByte(&bus);
    // 这里省略了将读取的数据转换为摄氏度的代码
}

需要注意的是，DS18B20的数据手册中推荐在发送转换命令之前先写入一个“Skip ROM”命令（0xCC），以确保总线上只有一个DS18B20设备。如果系统中有多个DS18B20设备，需要使用设备的ROM代码来选择特定的传感器进行读写。在采集数据时，还需要考虑到环境干扰、设备精度及校准等问题，确保数据的准确性。

# 2. 温度数据的基础算法处理

## 2.1 数字信号的滤波技术

### 2.1.1 常用滤波算法简介

在获取温度数据时，不可避免地会遇到噪声干扰，这将影响数据的准确性。为了解决这一问题，滤波技术应运而生。以下是一些在温度数据处理中常用的滤波算法：

- 移动平均滤波：通过计算一定数量的连续采样值的平均数，实现对噪声的平滑处理。简单而有效，但可能无法消除频率较高的噪声。
- 加权移动平均滤波：在移动平均滤波的基础上，给予更接近当前读数的采样点更高的权重，从而提高滤波效果。
- 指数平滑滤波：使用递归算法，对每个新读数赋予一个指数衰减的权重，较新数据赋予更高权重，旧数据则衰减更快。这种方法对最新数据的反应更快。

### 2.1.2 滤波算法在温度数据中的应用

考虑到温度数据通常变化缓慢，低通滤波技术尤其适用，以避免高频噪声的干扰。移动平均滤波器在这里是一个简单而实用的选择。下面是一个移动平均滤波器的Python实现代码：

def moving_average(data, n=3):
    filtered_data = []
    for i in range(len(data)):
        if i < n-1:
            filtered_data.append(data[i])
        else:
            filtered_data.append(sum(data[i-n+1:i+1])/n)
    return filtered_data

# 示例温度数据
temperature_data = [25.3, 25.4, 25.1, 25.5, 25.6, 25.7, 25.2, 25.3]

# 应用移动平均滤波器
filtered_data = moving_average(temperature_data)
print(filtered_data)

移动平均滤波器通过计算连续数据点的平均值来降低噪声的影响。此算法适用于数据变化不快，且对时间延迟不是特别敏感的情况。在对DS18B20传感器的温度数据应用此算法时，可以通过选择合适的点数`n`来平衡滤波效果和数据反应速度。

## 2.2 数据平滑处理

### 2.2.1 线性平滑与非线性平滑方法

数据平滑处理可以分为线性平滑和非线性平滑两大类。线性平滑方法主要包含移动平均和加权移动平均等，它们对数据进行线性组合，而不会改变数据的本质特征。非线性平滑方法则包括局部回归平滑、样条平滑等，这些方法在处理非线性数据时可能更为有效。

### 2.2.2 平滑处理对数据准确性的影响

尽管数据平滑可以有效减少噪声的影响，但是过度的平滑处理可能会导致数据失去一些重要的波动特性。这在某些需要精确分析变化趋势的应用中是不可取的。例如，在分析工业设备的温度曲线时，设备温度的突变可能预示着潜在的问题。因此，在选择平滑方法和参数时，需要在去噪和保持数据特性之间找到平衡。

## 2.3 异常值检测与处理

### 2.3.1 常见异常值检测算法

异常值指的是在一组数据中出现的不符合整体规律的数据点。检测异常值的方法有多种，比如箱线图法、标准差法、Z-分数法等。

- 箱线图法：通过数据的四分位数来确定异常值的范围。通常，小于四分位数Q1-1.5*IQR或大于四分位数Q3+1.5*IQR的值被认定为异常值。
- 标准差法：认为超出平均值±标准差范围的数据为异常值。这种方法适用于数据接近正态分布的情况。
- Z-分数法：计算每个数据点与平均值的差距，并除以标准差，得到Z-分数。一般而言，Z-分数大于3或小于-3的数据点被认为是异常值。

### 2.3.2 异常值处理策略和案例分析

处理异常值的策略有多种，最常见的是直接移除、修正、或者保留。不同的处理方法会影响后续的数据分析和决策。在温度数据处理中，移除或修正异常值前，需要仔细分析这些异常值产生的原因。

考虑以下真实案例：在一个工业热处理过程中，DS18B20传感器记录了一段时间内的温度数据。通过Z-分数法，发现了一个异常值，其Z-分数为-4.2，明显偏离正常范围。在调查原因后发现，这一异常值是在更换传感器时，由于环境温度波动过大造成的。因此，我们选择暂时移除这一数据点，并在后续的数据分析中对这段时期的温度稳定性进行特别关注。

通过本章节的介绍，我们学习了数字信号的滤波技术、数据平滑处理的原理与应用，以及异常值的检测与处理方法。下一章，我们将探讨更为高级的温度数据分析技术，包括趋势分析、统计学方法和机器学习技术的应用。

# 3. 高级温度数据分析技术

## 3.1 温度趋势分析
温度趋势分析是数据分析中的一个重要步骤，它可以帮助我们理解温度数据随时间变化的模式和规律。通过对历史数据的分析，我们可以预测未来可能出现的温度变化趋势，这对于很多领域，如天气预报、工业生产和环境控制等，都有着极其重要的意义。

### 3.1.1 趋势线拟合方法
趋势线拟合是统计学中用于确定变量之间关系的一种方法。它通过在一组数据点之间找到最佳拟合的线性或非线性关系，并用这条线来描述数据集的总体趋势。在温度数据分析中，常用的趋势线拟合方法包括线性回归、多项式回归、对数回归等。

下面展示一个简单的线性回归趋势线拟合的Python示例代码，其逻辑分析和参数说明将紧随代码块后。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 示例数据
x = np.array([1, 2, 3, 4, 5, 6, 7]).reshape((-1, 1))
y = np.array([1, 2, 1.3, 3.75, 2.25, 5.5, 3.5])

# 创建模型并拟合数据
model = LinearRegression()
model.fit(x, y)