【UQLab与MATLAB协同工作】：两种工具的深度集成与应用案例


参考资源链接：[UQLab安装与使用指南](https://wenku.csdn.net/doc/joa7p0sghw?spm=1055.2635.3001.10343)
# 1. UQLab与MATLAB协同工作基础

在本章中，我们将介绍UQLab与MATLAB协同工作所需要掌握的基础知识。UQLab是一个强大的不确定性量化（Uncertainty Quantification, UQ）工具箱，它是基于MATLAB的平台，专门用于不确定性和可靠性分析。本章将概述UQLab与MATLAB的集成基础，为后续章节中深入探讨具体的理论应用和实践操作奠定基础。

## 1.1 MATLAB作为基础平台

MATLAB是一个高级数值计算语言和交互式环境，广泛应用于工程计算、数据分析、算法开发等领域。其语言简洁、功能强大，使得它成为科学与工程领域中的标准工具。UQLab正是利用了MATLAB这一强大的计算能力和便捷的用户界面，为用户提供了一个易于操作的不确定性量化分析平台。

## 1.2 UQLab的安装与配置

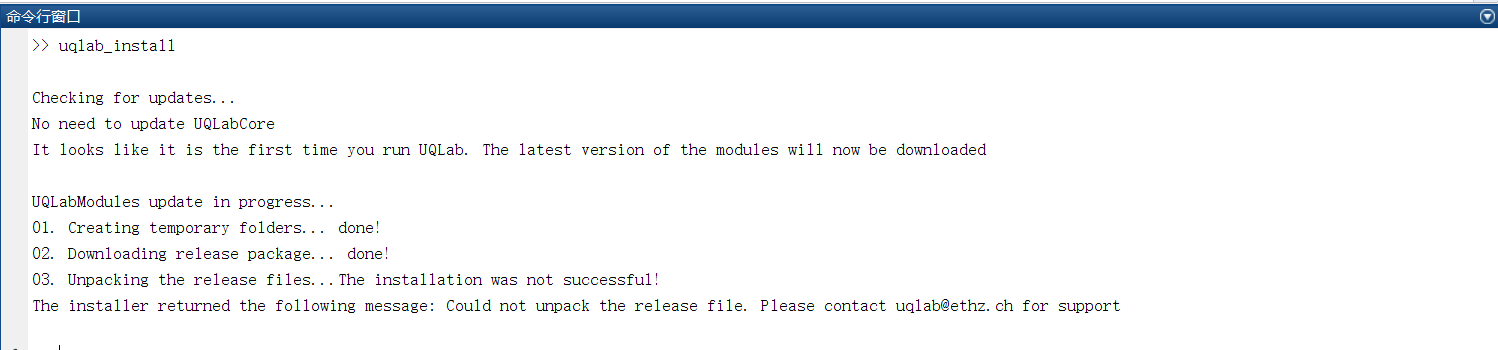
首先，您需要安装MATLAB环境，然后从UQLab的官方网站下载最新版本的UQLab。安装过程中，需要按照指引完成安装脚本的运行，并确保UQLab添加到MATLAB的路径中。完成安装后，通过简单的验证命令，可以确认UQLab是否成功安装并准备好使用。

% 在MATLAB命令窗口中运行以下命令以验证UQLab安装
uq_checkInstall

一旦安装和验证无误，您就可以开始探索UQLab提供的各种不确定性量化工具和功能了。这些功能包括但不限于不确定性模型的构建、敏感性分析、可靠性分析等。接下来的章节中，我们将详细探讨这些功能的具体应用和操作方法。

# 2. 理论基础与工具协同机制

## 2.1 概率论与随机变量

### 2.1.1 随机变量的基本概念

在概率论与统计学中，随机变量是一个基本而核心的概念，它是一个将随机试验的每一个可能结果映射到实数轴上的变量。随机变量的引入，为处理各种不确定性的数学问题提供了强有力的工具。在工程领域，例如，我们可能关心某一结构在特定条件下的响应，响应本身具有不确定性，我们将其视为一个随机变量。

为了深入理解随机变量，我们可以从它的类型开始。有离散随机变量和连续随机变量两种类型。离散随机变量可以取有限个或可数无限多个值，例如，投掷硬币的结果是离散的，只可能是正面或反面。而连续随机变量可以取任意值，通常在某个区间内取值，例如，物体在特定条件下的温度。

随机变量的另一个重要方面是它的分布，它决定了随机变量取各个值的概率。对于离散随机变量，我们通常通过概率质量函数（Probability Mass Function，PMF）来描述其分布。对于连续随机变量，则使用概率密度函数（Probability Density Function，PDF）来描述。在UQLab中，我们可以利用特定的函数接口来定义随机变量，进而进行后续的概率分布分析。

### 2.1.2 概率分布与特征

当随机变量的分布类型确定后，我们就可以计算其概率分布函数（Cumulative Distribution Function，CDF），CDF表示随机变量小于或等于某一特定值的概率。对于连续随机变量，CDF是PDF的积分，对于离散随机变量，CDF是PMF的累加和。

除了概率分布函数，随机变量还有一系列特征值，如期望、方差、偏度和峰度等，它们可以提供随机变量分布的附加信息。期望值（或均值）可以看作是随机变量的平均取值，方差度量的是随机变量取值的离散程度，偏度描述的是分布的对称性，而峰度反映了分布的“尖峭”或“平缓”程度。

在UQLab中，我们可以用一系列函数来计算这些特征值。例如，对于正态分布的随机变量，UQLab提供了`uq_getStatisticalMoments`等函数来计算这些统计特征。这些函数背后通常都对应着一些数学公式和算法，用户可以在UQLab的文档中找到相应的解释和示例。

### 2.1.3 随机变量的操作

在概率论中，随机变量之间的运算也是十分重要的，比如加法、乘法等。根据随机变量的独立性，我们可以确定运算后新随机变量的分布。例如，两个独立同分布的正态随机变量之和也是正态分布的。UQLab通过特定的函数，如`uq_sum`，可以方便地对随机变量进行这些运算。

使用UQLab时，用户可以结合MATLAB强大的数值计算能力，利用这些函数进行概率模型的构建和分析。这为处理含有不确定性的复杂系统提供了有效的数学工具，使得分析不确定性影响更加方便和直观。

## 2.2 UQLab与MATLAB的集成基础

### 2.2.1 UQLab简介与安装

UQLab是基于MATLAB的不确定性量化（Uncertainty Quantification，UQ）工具箱，它为用户提供了一个强大而灵活的环境，以处理各种不确定性问题。UQLab专门针对那些需要进行高级不确定性分析的工程师和研究人员设计，提供了从基本的概率模型到复杂的可靠性分析和灵敏度分析的全套解决方案。

安装UQLab相对简单，您只需将下载的UQLab文件夹复制到MATLAB的工作路径或者添加到MATLAB的路径中即可。安装完成后，通过在MATLAB命令窗口中输入`uq_init`，即可完成UQLab的初始化。这一步骤会自动检查UQLab是否可以正常运行，包括依赖的MATLAB工具箱是否安装。

UQLab的初始化还会导入一系列的工具箱和文件，为不确定性量化分析提供必要的支持。初始化过程中可能会提示用户下载并安装一些额外的MATLAB工具箱，因为UQLab在某些高级功能上依赖于这些工具箱。用户在安装时应确保互联网连接稳定，以便顺利完成下载和安装。

### 2.2.2 MATLAB与UQLab的接口

MATLAB提供了与UQLab交互的接口，使得UQLab可以方便地整合到用户已有的MATLAB工作环境中。这不仅允许用户利用MATLAB现有的函数和功能，还能够将UQLab的数据和模型输出整合到自己的研究中。

MATLAB和UQLab之间的接口主要通过UQLab提供的各类函数实现。例如，我们可以直接调用UQLab的`uq_setPrior`函数来设定一个随机变量的先验分布，然后使用`uq_sample`函数来生成该先验分布的样本。这些函数执行后会返回一个UQ Sample结构体，里面包含了所有生成样本的详细信息，包括样本值、概率权重等。

在使用这些接口时，用户需要对UQLab的函数库有一定的了解，因为不同的函数通常对应不同的UQ任务。用户可以通过阅读UQLab的官方文档来获取相关函数的详细信息和使用示例。例如，`uq_setPrior`函数需要用户提供一些参数，如分布类型、分布参数等。用户在使用时应该根据自己的具体问题来设置这些参数。

## 2.3 理论与实际应用的桥梁

### 2.3.1 UQLab中的概率模型

UQLab提供了丰富的概率模型，从常见的分布如正态分布、均匀分布到更复杂的相关随机过程，用户可以在这些模型的基础上构建自己的不确定性分析。为了更好地理解和使用这些概率模型，用