【MATLAB时间序列特征工程】：构建预测信号的6大步骤

# 1. 时间序列分析基础

在本章节中，我们将引入时间序列分析的初始概念，为读者构建一个坚实的理解基础。首先，我们会探讨时间序列数据的特点，包括时间依赖性和趋势、季节性等周期性行为。随后，我们会介绍基本的时间序列分析术语和概念，例如时间点、频率、观测值，以及时间序列的类型，如平稳序列与非平稳序列。最后，我们将简要描述时间序列分析的主要目的——预测未来的观测值和识别数据中的模式。本章旨在为后面更深层次的讨论打下基础，确保即便是初学者也能跟上步伐。

- 时间点：时间序列中的每个数据点都与特定时间相关联。
- 频率：时间序列中观测值收集的速率，例如每分钟、每天或每月。
- 平稳序列：其统计特性不随时间变化的序列。

通过阅读本章内容，读者将能够了解时间序列分析的基本原理，并为学习更高级的主题奠定基础，如数据预处理、特征选择和应用。

# 2. 数据预处理技术

### 2.1 数据清洗

#### 2.1.1 处理缺失值

处理缺失值是时间序列分析中常见的数据预处理步骤。在实际应用中，数据收集过程可能由于各种原因导致记录不完整。有效的缺失值处理方法能够减少数据质量问题，提高分析和预测模型的准确度。

在MATLAB中，处理缺失值的方法多种多样。最简单的方法之一是删除含有缺失值的行。例如，使用 `rmmissing` 函数可以轻松删除数据集中的缺失值：

% 假设 A 是一个时间序列数据矩阵，其中含有缺失值
A(missing(A)) = []; % 删除含有缺失值的行

另一种常见的方法是填充缺失值，比如可以用均值、中位数或前一个观察值填充。在MATLAB中，可以使用 `fillmissing` 函数进行更复杂的缺失值填充：

% 使用线性插值填充缺失值
B = fillmissing(A, 'linear');

### 2.1.2 去除异常值

异常值可能会扭曲数据的分布，导致时间序列分析结果不可靠。为了确保数据质量，识别和去除异常值是关键步骤。异常值可以使用统计方法来识别，如箱线图方法，该方法基于数据的四分位数定义异常值。

在MATLAB中，可以利用箱线图的概念来确定异常值的界限，并去除它们：

% 假定 A 是一个时间序列向量
Q1 = quantile(A, 0.25); % 第一四分位数
Q3 = quantile(A, 0.75); % 第三四分位数
IQR = Q3 - Q1; % 四分位距

% 定义异常值的界限
lower_bound = Q1 - 1.5 * IQR;
upper_bound = Q3 + 1.5 * IQR;

% 找到并去除异常值
outliers = A < lower_bound | A > upper_bound;
B = A(~outliers); % 结果数据集

去除异常值后，数据集更加稳定，有利于后续的分析步骤。

### 2.2 数据转换

#### 2.2.1 标准化与归一化

标准化和归一化是数据预处理中常用的两种数据转换方法。它们的目标是将数据转换到一个标准的范围内，以便于分析和比较。标准化通常指的是将数据按比例缩放，使之落入一个标准的正态分布中，而归一化则是将数据缩放到一个指定的范围，如0到1之间。

在MATLAB中可以使用 `zscore` 函数进行标准化：

% 假设 C 是需要标准化的时间序列数据向量
C_standardized = zscore(C);

归一化可以使用以下公式进行计算：

% 将 C 归一化到[0,1]范围内
C_min = min(C);
C_max = max(C);
C_normalized = (C - C_min) / (C_max - C_min);

#### 2.2.2 差分与平滑技术

差分和移动平均是时间序列分析中用来去除数据趋势和季节性的常用技术。差分是将当前数据点减去前一个数据点的过程，而移动平均则是计算连续数据点的滑动窗口平均值。

在MATLAB中，差分可以通过减法运算直接实现：

% 假设 D 是原始时间序列数据向量
D_diff = diff(D); % 一次差分

对于移动平均，可以使用 MATLAB 的 `movmean` 函数：

% 使用3点移动平均平滑时间序列数据
D_moving_avg = movmean(D, [3 1]); % 3点向前和向后平均

通过差分和移动平均，可以有效地减少时间序列数据中的噪音，并平滑数据趋势，使得分析更加清晰。

### 2.3 特征抽取

#### 2.3.1 时域特征

时域特征是指从时间序列的原始观测值中直接提取的统计特征。这些特征可以是简单的统计量，如均值、标准差、偏度和峰度，也可以是更复杂的特征，如自相关系数和偏自相关系数。

在MATLAB中，可以使用以下方法提取时域特征：

% 计算均值和标准差
mean_D = mean(D);
std_D = std(D);

% 计算偏度和峰度
skewness_D = skewness(D);
kurtosis_D = kurtosis(D);

% 计算自相关和偏自相关系数
[acf, lags] = autocorr(D);
[pacf, lags] = parcorr(D);

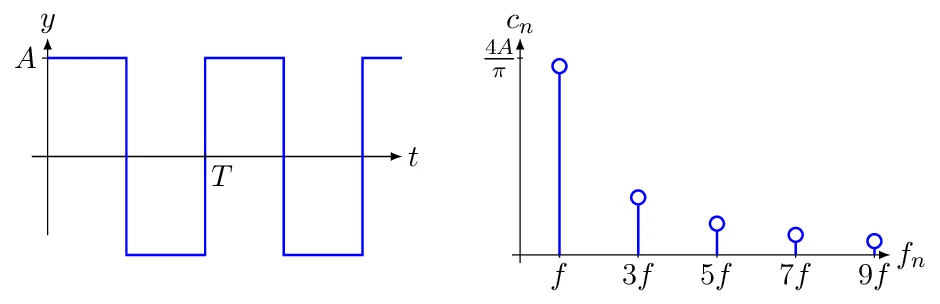
#### 2.3.2 频域特征

频域特征是通过傅里叶变换从时间序列中抽取的特征。傅里叶变换可以将时间序列从时域转换到频域，从而识别出时间序列中的周期性成分。

在MATLAB中，可以使用 `fft` 函数进行快速傅里叶变换：

% 计算 D 的傅里叶变换并取绝对值的平方，得到功率谱密度
D_fft = fft(D);
D_psd = abs(D_fft).^2;

通过提取频域特征，可以更好地理解时间序列数据背后的周期性模式，从而对数据进行有效的分析。

# 3. 特征选择方法

在时间序列分析中，特征选择是一个至关重要的步骤，它旨在减少数据集的维度，同时保留或增强模型的预测能力。特征选择不仅有助于避免过拟合，还可以提高模型的训练速度和预测效率。本章将深入探讨各种特征选择技术，包括统计测试方法、信息论方法以及基于模型的选择技术。

## 3.1 统计测试方法

统计测试方法依赖于统计假设检验，以确定特征与目标变量之间的关联性。最常用的方法包括相关性分析和假设检验。

### 3.1.1 相关性分析

相关性分析是评估两个变量之间线性关系强度和方向的统计工具。皮尔逊相关系数是最常见的度量方式，其值介于-1和1之间。值为1表示完全正相关，-1表示完全负相关，0表示没有线性相关。在时间序列分析中，相关性分析可以帮助我们理解不同时间点之间数据的关联性。

import numpy as np
import pandas as pd
from scipy.stats import pearsonr

# 示例数据集
data = pd.DataFrame({
    'time_series_1': np.random.randn(100),
    'time_series_2': np.random.randn(100)
})

# 计算时间序列1和时间序列2之间的相关系数
correlation, p_value = pearsonr(data['time_series_1'], data['time_series_2'])

print(f"相关系数: {correlation}, P值: {p_value}")

在上述代码中，我们首先生成了两个随机的正态分布时间序列，并使用`pearsonr`函数计算它们之间的相关系数和P值。根据P值，我们可以判断相关性是否具有统计学意义。

### 3.1.2 假设检验

假设检验常用于确定样本统计量是否具有足够的证据支持一个关于总体参数的断言。在特征选择中，我们常常使用t检验或F检验来评估特征与目标变量之