erfc函数在概率论中的秘密武器：正态分布与累积分布函数

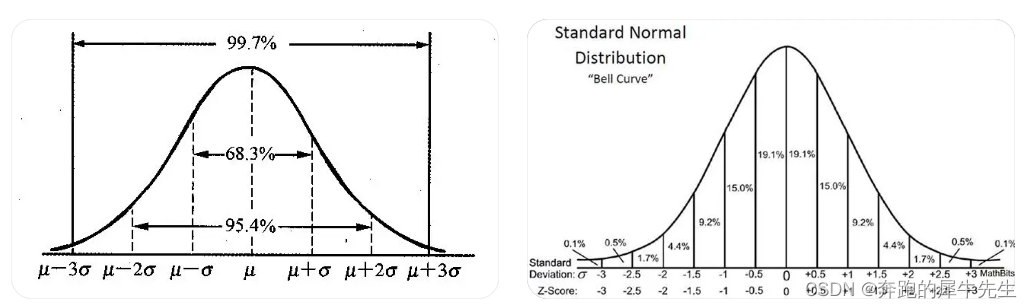
# 1. 正态分布与累积分布函数

正态分布，又称高斯分布，是一种连续概率分布，其概率密度函数为：

f(x) = (1 / (σ * √(2π))) * exp(-(x - μ)² / (2σ²))

其中，μ为均值，σ为标准差。

累积分布函数 (CDF) 给出了一个随机变量小于或等于给定值的概率。对于正态分布，CDF 为：

F(x) = ∫_{-∞}^{x} f(t) dt = (1 / 2) * (1 + erf((x - μ) / (σ * √(2))))

其中，erf 为互补误差函数，定义为：

erf(x) = (2 / √(π)) * ∫_{0}^{x} exp(-t²) dt

# 2. erfc函数的数学基础

### 2.1 互补误差函数的定义和性质

互补误差函数（erfc），又称互补高斯误差函数，定义为：

erfc(x) = 1 - erf(x) = 1 - (2/√π) ∫0^x e^(-t^2) dt

其中，erf(x) 是误差函数。

erfc函数具有以下性质：

- **对称性：** erfc(-x) = 2 - erfc(x)
- **渐近性：** 当 x → ∞ 时，erfc(x) → 0；当 x → -∞ 时，erfc(x) → 2
- **奇偶性：** erfc(x) 是偶函数，即 erfc(-x) = erfc(x)

### 2.2 erfc函数与正态分布的关系

erfc函数与正态分布密切相关。标准正态分布的累积分布函数（CDF）可以表示为：

Φ(x) = (1/2) [1 + erf(x/√2)]

因此，erfc函数可以用来计算标准正态分布的补集概率：

P(X > x) = erfc(x/√2)

这个关系在概率论和统计学中非常有用，因为它允许我们使用erfc函数来计算正态分布中特定区域的概率。

# 3. erfc函数在概率论中的应用

### 3.1 概率密度函数的计算

erfc函数在概率论中的一大应用是计算正态分布的概率密度函数（PDF）。正态分布的PDF由以下公式给出：

f(x) = (1 / (σ * sqrt(2 * π))) * exp(-(x - μ)² / (2 * σ²))

其中：

* x 是随机变量
* μ 是均值
* σ 是标准差

使用erfc函数，可以将正态分布的PDF表示为：

f(x) = (1 / (σ * sqrt(2 * π))) * erfc((x - μ) / (σ * sqrt(2)))

### 3.2 累积分布函数的计算

erfc函数还可以用于计算正态分布的累积分布函数（CDF）。CDF给出了随机变量小于或等于给定值的概率。正态分布的CDF由以下公式给出：

F(x) = (1 / 2) * (1 + erf((x - μ) / (σ * sqrt(2))))

其中：

* x 是随机变量
* μ 是均值
* σ 是标准差

使用erfc函数，可以将正态分布的CDF表示为：

F(x) = 1 - (1 / 2) * erfc((x - μ) / (σ * sqrt(2)))

### 3.3 置信区间和假设检验

erfc函数在概率论中另一个重要的应用是计算置信区间和进行假设检验。置信区间是估计总体参数（如均值或标准差）的范围。假设检验用于确定数据是否支持给定的假设。

在置信区间计算中，erfc函数用于计算正态分布中给定概率下的临界值。假设检验中，erfc函数用于计算p值，即观察到的数据与假设之间差异的概率。

# 4. erfc函数的数值计算

### 4.1 近似公式和算法

由于erfc函数的解析形式复杂，在实际应用中通常使用近似公式或算法来进行数值计算。常用的近似公式包括：

- **泰勒级数展开：**

erfc(x) ≈ 1 - (2/√π) ∑_{n=0}^∞ (-1)^n (2n)! / (n! (2n+1)) x^(2n+1)

- **渐近展开：**

erfc(x) ≈ exp(-x^2) / (x√π) [1 + 1/(2x^2) + 3/(4x^4) + 15/(8x^6) + ...]

- **收敛较快的近似公式：**

erfc(x) ≈ exp(-x^2) / (x√π) [1 + 2/(x^2-1) + 10/(x^2-4) + 42/(x^2-9) + ...]

对于不同范围的x值，不同的近似公式具有不同的精度。泰勒级数展开在x较小时精度较高，而渐近展开在x较大时精度较高。收敛较快的近似公式在整个x值范围内都具有较好的精度。

除了近似公式，还有各种算法可以用来计算erfc函数。其中一种常用的算法是**高斯求积法**。该算法将erfc函数的积分表示为一个有限和，并使用高斯积分点来近似积分。

### 4.2 计算精度和误差分析

在使用近似公式或算法计算erfc函数时，需要考虑计算精度和误差。

**计算精度**取决于所使用的近似公式或算法的精度。对于不同的x值范围，不同的近似公式或算法具有不同的精度。

**误差分析**可以用来估计计算误差的大小。一种常用的误差分析方法是**相对误差**，它定义为：

相对误差 = |近似值 - 真实值| / |真实值|

通过计算相对误差，可以评估近似公式或算法的精度。

**代码块：**

import math

# 使用泰勒级数展开计算erfc函数
def erfc_taylor(x, n=10):
    """
    使用泰勒级数展开计算erfc函数。

    参数：
        x: 输入值
        n: 展开项数

    返回：
        erfc(x)的近似值
    """
    result = 1
    for i in range(1, n+1):
        result -= (2/math.sqrt(math.pi)) * ((-1)**i) * math.factorial(2*i) / (math.factorial(i) * math.factorial(2*i+1)) * x**(2*i+1)
    return result

# 使用高斯求积法计算erfc函数
def erfc_quad(x, n=10):
    """
    使用高斯求积法计算erfc函数。

    参数：
        x: 输入值
        n: 积分点数

    返回：
        erfc(x)的近似值
    """
    from scipy.integrate import quad
    def integrand(t):
        return math.exp(-t**2)
    a, b = 0, x
    result, error = quad(integrand, a, b, n=n)
    return 2 * result / math.sqrt(math.pi)

# 计算相对误差
def relative_error(approx, true):
    """
    计算相对误差。

    参数：
        approx: 近似值
        true: 真实值

    返回：
        相对误差
    """
    return abs(approx - true) / abs(true)

# 测试不同方法的精度
x_values = [0.1, 0.5, 1.0, 2.0, 5.0]
for x in x_values:
    true_value = math.erfc(x)
    approx_taylor = erfc_taylor(x)
    approx_quad = erfc_quad(x)
    print(f"x = {x}")
    print(f"True value: {true_value}")
    print(f"Taylor approximation: {approx_taylor}")
    print(f"Gauss quadrature approximation: {approx_quad}")
    print(f"Relative error (Taylor): {relative_error(approx_taylor, true_value)}")
    print(f"Relative error (Gauss quadrature): {relative_error(approx_quad, true_value)}")
    print()

**代码逻辑分析：**

该代码块实现了使用泰勒级数展开和高斯求积法计算erfc函数的函数。还实现了计算相对误差的函数。

主程序部分测试了不同方法在不同x值下的精度。它打印了真实值、近似值和相对误差。

**参数说明：**

- `erfc_taylor(x, n)`：使用泰勒级数展开计算erfc函数，其中`x`是输入值，`n`是展开项数。
- `erfc_quad(x, n)`：使用高斯求积法计算erfc函数，其中`x`是输入值，`n`是积分点数。
- `relative_error(approx, true)`：计算相对误差，其中`approx`是近似值，`true`是真实值。

# 5. erfc函数在实际问题中的应用

erfc函数在实际问题中有着广泛的应用，涉及到风险评估、金融建模、材料科学、工程学、生物统计学和医学研究等多个领域。

### 5.1 风险评估和金融建模

在风险评估和金融建模中，erfc函数常用于计算金融资产的价值、风险和收益率。例如，在期权定价中，erfc函数用于计算期权的Black-Scholes公式，该公式用于估算期权的公平价值。

import numpy as np

# 计算期权的Black-Scholes公式
def black_scholes(S, K, r, sigma, t):
    d1 = (np.log(S / K) + (r + sigma**2 / 2) * t) / (sigma * np.sqrt(t))
    d2 = d1 - sigma * np.sqrt(t)
    return S * np.exp(-r * t) * scipy.stats.norm.cdf(d1) - K * np.exp(-r * t) * scipy.stats.norm.cdf(d2)

# 参数说明：
# S: 标的资产价格
# K: 执行价格
# r: 无风险利率
# sigma: 波动率
# t: 到期时间

### 5.2 材料科学和工程学

在材料科学和工程学中，erfc函数用于模拟材料的扩散和热传导过程。例如，在半导体器件的制造中，erfc函数用于计算掺杂剂在半导体中的扩散分布。

import matplotlib.pyplot as plt

# 模拟掺杂剂在半导体中的扩散分布
def diffusion(D, t, x):
    return (D * t / np.pi)**0.5 * np.exp(-x**2 / (4 * D * t))

# 参数说明：
# D: 扩散系数
# t: 扩散时间
# x: 距离

# 绘制扩散分布图
plt.plot(x, diffusion(1e-12, 10, x))
plt.xlabel("距离 (μm)")
plt.ylabel("掺杂剂浓度")
plt.show()

### 5.3 生物统计学和医学研究

在生物统计学和医学研究中，erfc函数用于分析生存数据、计算统计显著性和进行诊断测试。例如，在生存分析中，erfc函数用于计算患者生存率的Kaplan-Meier曲线。

import lifelines

# 计算Kaplan-Meier曲线
def kaplan_meier(T, E):
    # T: 生存时间
    # E: 事件指示器（0 表示未发生事件，1 表示发生事件）
    km = lifelines.KaplanMeierFitter()
    km.fit(T, E)
    return km.survival_function_

# 绘制Kaplan-Meier曲线
plt.plot(km.event_table['time'], km.survival_function_)
plt.xlabel("生存时间")
plt.ylabel("生存率")
plt.show()