【阀门流量特性曲线解读：高效应用指南】


# 摘要
阀门流量特性曲线是描述阀门在不同开度下流体流量变化的关键指标，对于工业阀门的选型和系统设计至关重要。本文综述了流量特性曲线的理论基础、数学模型以及测量和分析方法。详细探讨了流量特性曲线在阀门选型指导、系统性能优化和故障诊断中的应用，并分析了智能控制系统、数字孪生技术等现代技术应用。通过行业案例研究与实践技巧分享，本文旨在提高工程师对流量特性曲线的理解和应用能力，以实现系统性能提升和能源效率优化。

# 关键字
流量特性曲线；流量控制；系统设计；智能控制系统；数字孪生；节能降耗

参考资源链接：[阀门流量计算方法说明文件](https://wenku.csdn.net/doc/4cyqhxhs92?spm=1055.2635.3001.10343)
# 1. 阀门流量特性曲线概述

## 1.1 阀门的定义和作用

在工业控制系统中，阀门是执行元件之一，用于调节和控制流体的流量、压力和方向。其主要作用是启动或停止流体的流动，或控制流体在一定范围内的流动量，从而满足工艺过程的要求。

## 1.2 流量特性曲线的重要性

流量特性曲线是阀门性能的重要体现，它展示了阀门开度与流经阀门的流体流量之间的关系。通过理解流量特性曲线，工程师可以预测和控制流体的流动情况，对于系统的稳定运行和性能优化至关重要。

## 1.3 阀门流量特性曲线的种类

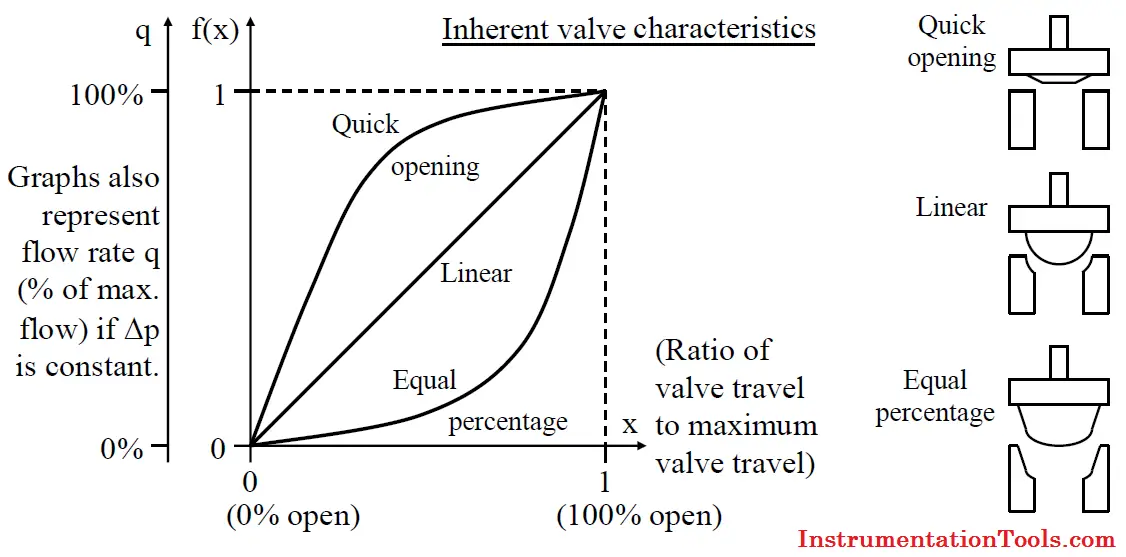
根据不同的设计和工作原理，阀门可以展示不同的流量特性曲线。常见的有线性流量特性、等百分比流量特性、快开流量特性等。选择合适的阀门和流量特性曲线，是确保系统高效、稳定运行的前提。

通过这一章的概述，我们将为进一步深入探讨流量特性曲线的理论基础和应用打下坚实的基础。接下来，我们将深入探讨流量特性曲线的数学模型，以及如何利用这些理论来测量、分析和应用这些曲线。

# 2. 理论基础：流量特性曲线的数学模型

## 2.1 流体动力学基础

流体动力学是研究流体运动规律及其与固体边界相互作用的基础学科。在流量特性曲线的研究中，理解流体动力学的基本原理是至关重要的。

### 2.1.1 流体流动的基本原理

流体流动的基本原理涉及到流体的连续性方程和伯努利方程。连续性方程表达了流体在流动过程中，某一截面上的质量流量保持不变的规律，其数学表达形式为：

A1 * V1 = A2 * V2

其中，`A` 表示截面积，`V` 表示流速。这意味着当流体通过管道时，截面积越大，流速越小；反之亦然。

伯努利方程则是一个能量守恒的表达式，它结合了流体的压力能、动能和位能，可以表达为：

P1 + 1/2 * ρ * V1^2 + ρ * g * h1 = P2 + 1/2 * ρ * V2^2 + ρ * g * h2

其中，`P` 是压强，`ρ` 是流体密度，`g` 是重力加速度，`h` 是高度，下标 1 和 2 表示不同的位置。伯努利方程可以解释流体在流动过程中能量的转换。

### 2.1.2 压力损失与流速的关系

流体在流动过程中，由于摩擦和湍流等因素会产生压力损失。压力损失的数学模型可以通过达西-魏斯巴赫公式表示：

ΔP = f * (L/D) * (ρ * V^2 / 2)

其中，`ΔP` 表示压力损失，`f` 是摩擦因子，`L` 是管道长度，`D` 是管道直径，`ρ` 是流体密度，`V` 是流速。

## 2.2 流量特性曲线的定义

流量特性曲线是表达流体流过阀门时流量与阀位开度或压差之间关系的曲线。它对于阀门的设计、选型和系统性能分析至关重要。

### 2.2.1 流量特性曲线的类型

根据流体流过阀门时流量与阀位开度的关系，流量特性曲线可以分为线性、快开、等百分比等几种类型。其中，线性流量曲线表示流量与阀位开度成正比；快开曲线在阀位开度较小时流量变化迅速，随着开度增加，流量变化趋于缓慢；等百分比曲线则保证流量变化率与开度成恒定的百分比关系。

### 2.2.2 特性曲线中的关键参数

流量特性曲线中的关键参数包括流星系数（Cv/Kv）、压差比（ΔP/P1）等。流量系数是指在单位压差下，流过阀门的流量；压差比是指在特定开度下，阀门两端的压差与进口压差的比值。

## 2.3 流量特性曲线的数学表达

流量特性曲线的数学表达形式对于其分析和应用具有重要指导意义。不同类型的流量曲线有着不同的数学模型。

### 2.3.1 线性流量曲线的数学模型

对于线性流量曲线，其数学模型相对简单，可以表达为：

Q = Q0 * X

其中，`Q` 是流量，`Q0` 是最大流量，`X` 是阀位开度（以百分比表示），假设流量与阀位开度成正比。

### 2.3.2 非线性流量曲线的数学模型

对于非线性流量曲线，如等百分比或快开曲线，数学模型通常较为复杂。以等百分比流量曲线为例，其表达式为：

Q = Q0 * (X/100)^n

其中，`n` 是大于1的常数，它决定了流量曲线的形状。这种曲线保证了流量变化率与开度成恒定的百分比关系，使得流体流量的调节更加精确和稳定。

# 3. 流量特性曲线的测量与分析

流量特性曲线是流体工程中对控制元件性能评估的重要工具。准确地测量和分析这些曲线对于系统设计、性能优化以及故障诊断至关重要。本章将深入探讨流量特性曲线的测量技术、数据分析方法，并通过实际案例分析展示如何应用这些曲线。

## 3.1 测量技术

### 3.1.1 常用的流量测量设备

流量测量是通过使用特定的设备来确定流体流动速率的过程。以下是一些常用的流量测量设备：

1. 差压流量计：通过测量管道两侧的压力差来计算流量。伯努利方程是其理论基础，常见的差压流量计包括孔板流量计、文丘里管和弯管流量计等。
2. 电磁流量计：基于法拉第电磁感应定律，适用于导电流体，通过测量管内流体产生的感应电压来确定流速。
3. 涡轮流量计：使用涡轮叶片旋转的频率来推算流量，适用于清洁流体。
4. 超声波流量计：利用