深度解析cforest包参数调优：R语言预测准确性的关键一步

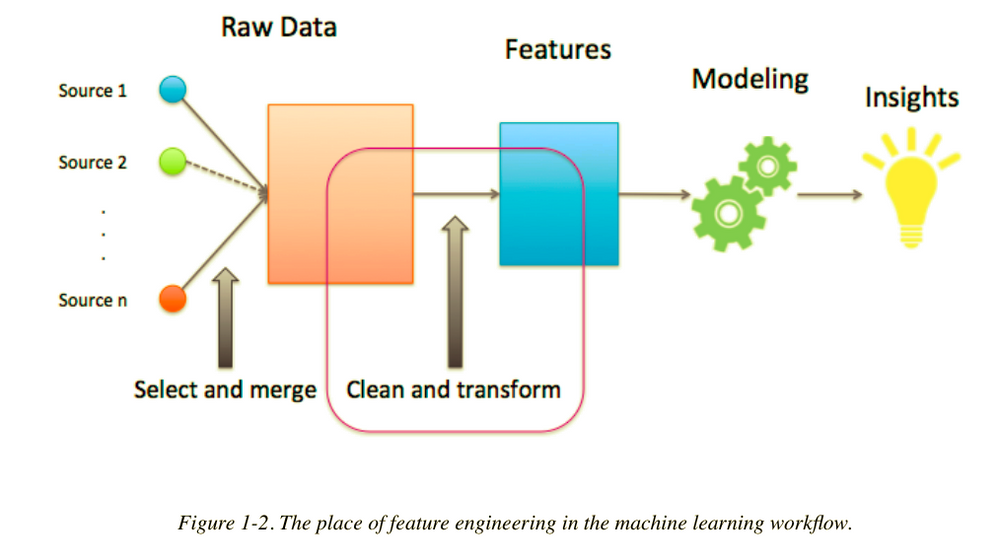
# 1. cforest包概览

在机器学习领域，集成学习方法通过组合多个模型来提升预测性能和稳定性，已成为一项重要的技术手段。其中，`cforest`包是R语言中实现条件推断森林（Conditional Inference Forests）的工具，该算法在保持随机森林的优秀特性的同时，通过条件推断来避免过拟合，并提高模型的准确性和可靠性。本章将介绍`cforest`包的基本概念，为读者提供一个初步的了解，为进一步深入学习cforest算法及其在R语言中的应用打下基础。

## 1.1 cforest的定义与特点
`cforest`是一种基于条件推断的决策树集成学习方法，它在构建单个决策树时引入了非参数的统计检验，确保了变量选择的客观性和统计性，从而更合理地捕捉数据的结构。这种算法特别适合处理存在复杂交互关系的数据集。

## 1.2 cforest与R语言的关联
由于`cforest`包是专为R语言设计的，它的安装与使用都非常简单。在R的控制台中，用户仅需输入简单的代码即可调用cforest包进行数据分析和模型训练，无需复杂配置。R语言的灵活性和丰富的数据处理功能也使得cforest的应用范围更为广泛。

## 1.3 cforest在实际问题中的应用场景
由于其独特的特征和算法优势，`cforest`被广泛应用于生物信息学、金融风险评估、环境科学等领域，尤其适合处理高维数据、类别变量和存在非线性关系的问题。

# 安装cforest包
install.packages("party")

# 加载cforest包，并使用它来训练一个模型
library(party)
model_cforest <- cforest(Survived ~ ., data = Titanic, control = cforest_unbiased(mtry = 3, ntree = 200))

以上代码展示了如何在R环境中安装并加载`cforest`包，然后使用它对泰坦尼克号数据集进行生存预测的简单示例。本章的介绍为后续章节深入探讨cforest的算法原理、参数调优和高级应用奠定了基础。

# 2. 理解cforest算法原理

## 2.1 随机森林与cforest

### 2.1.1 随机森林基础

随机森林（Random Forest）是一种集成学习算法，它通过构建多个决策树并将它们的预测结果进行汇总来提高整体预测的准确性。在随机森林中，每一棵树都是在原始数据集的一个随机子样本上训练而成，并且在每个分裂点处只考虑随机选取的一组特征，从而实现特征的随机性。这种方法有效地减少了模型的方差，并防止过拟合，使得模型具有较好的泛化能力。

随机森林中的每棵树都是独立训练的，这意味着它们可以并行处理，提高算法的运行效率。同时，这种独立性也为模型带来了额外的多样性。随机森林在分类和回归任务中都有广泛的应用，尤其是当数据集较大时，随机森林往往能取得不错的效果。

### 2.1.2 cforest与随机森林的区别

cforest是随机森林的一种变体，它通过在特征抽样（feature bagging）的基础上，还采用了样本抽样（case bagging）来进一步增加单棵树之间的多样性。这种样本抽样通常是通过不放回抽样实现的，即从训练集中随机抽取一定数量的样本，构建一棵树后这些样本将从原始训练集中移除。

cforest与随机森林的一个关键区别在于，cforest在构建每棵树时使用了条件推断树（conditional inference trees），而不是传统的决策树。条件推断树通过统计测试来选择最佳分割变量和分割点，这可以避免变量选择偏差，并使单棵树更加稳定。此外，cforest在处理不平衡数据集或存在类别不平衡时表现更佳，因为不放回抽样有助于保持样本分布的一致性。

## 2.2 cforest算法核心概念

### 2.2.1 不放回抽样与放回抽样

在随机森林算法中，放回抽样是一种常见的做法，即在构建每一棵树的训练集时，原始数据集中的样本可以被重复选择。然而，cforest算法采用的是不放回抽样，意味着在构建每一棵树时，一旦样本被选中，它就不会再次出现在其他树的训练集中。这种方法在处理大规模数据集时可以提供更好的样本多样性，因为数据集中的每个样本只能用于构建一棵树。

不放回抽样虽然在单棵树之间引入了更多的多样性，但也有可能导致样本不足的问题，尤其是在原始数据集中每个类别数量较少的情况下。因此，使用cforest时需要格外注意数据集的大小和类别分布情况，以确保算法的有效性。

### 2.2.2 特征抽样与样本抽样的实现

cforest算法中的特征抽样（feature bagging）是指在树的每个分裂节点选择一个随机特征子集来考虑，这与随机森林中的做法相似。但是，cforest在样本抽样上引入了创新，即通过不放回抽样实现的样本多样性的增加。

为了实现不放回抽样，可以在构建每棵树之前，首先从原始数据集中随机选择一个大小为N的样本子集，其中N通常小于原始数据集的总样本数。使用这个子集来训练一棵树，然后将这些样本从原始数据集中移除，再选择下一个子集来训练下一棵树。这个过程重复进行，直到构建了所需数量的树。

## 2.3 cforest的数学模型

### 2.3.1 集成学习的数学基础

集成学习是一种机器学习范式，它通过构建并结合多个学习器来提高预测性能和稳定性的方法。集成学习的关键在于组合不同学习器的预测结果以得到更好的整体性能。

数学上，假设有一个预测器集合 \(\{f_1(x), f_2(x), ..., f_k(x)\}\)，其中 \(f_i(x)\) 是第 \(i\) 个模型的预测结果，那么集成学习的目标是找到一个最优的组合函数 \(F(x)\)，使得在某种意义上 \(F(x)\) 的性能优于任何单独的 \(f_i(x)\)。

假设每个模型 \(f_i(x)\) 的误差为 \(e_i\)，那么通过组合多个模型可以减少总体误差 \(E\)。如果每个模型的预测是独立的，那么最优的线性组合可以通过以下公式实现：

\[ F(x) = \frac{1}{k}\sum_{i=1}^{k}f_i(x) \]

然而，实际情况中，模型间的独立性很难保证，因此需要更复杂的方法来优化组合策略，以减少集成的总体误差。

### 2.3.2 cforest的树构造过程

cforest算法中树的构造过程使用了条件推断树的方法，条件推断树是基于统计检验来选择最优的分割变量和分割点，从而避免了传统决策树在变量选择上的随机性问题。

具体而言，对于每个分裂点，条件推断树会计算所有特征与响应变量之间的关联性，然后选取关联性最强的特征进行分割。这种方法通过统计测试确保了分割点的统计显著性，有助于提升单棵树的稳定性和解释性。

在cforest中，这个过程是在特征和样本的双重抽样背景下进行的。对于每个分裂点，算法首先从随机选取的特征子集中选出最优特征，然后基于该特征和统计测试确定最优的分裂点。如此重复，直到树达到预设的深度或者不能再继续分裂为止。

接下来，通过类似的过程继续构建下一棵树，直到达到预设的树的数量。最后，cforest的预测是通过平均每棵树的预测结果来实现的，如果是分类问题，则采用投票机制。

### 2.3.3 代码实现

以下是使用`party`包在R语言中实现cforest的代码示例：

library(party)

# 假设我们有训练数据集 train_data 和对应的标签 train_label
# 构建cforest模型
cforest_model <- cforest(target ~ ., data = train_data, control = cforest_unbiased(mtry = 2))

# 使用模型对测试集进行预测
predictions <- predict(cforest_model, newdata = test_data)

在这段代码中，`cforest`函数构建了一个条件推断森林模型。参数`target ~ .`指定了目标变量和特征变量的关系，`mtry`参数指定了每个节点尝试的变量数，这里设置为2，意味着每次分裂时会考虑两个特征进行最佳分割点的选择。最后，使用`predict`函数进行预测，`newdata`参数指定了要预测的数据集。

# 3. cforest参数详解

## 3.1 参数设置的重要性
### 3.1.1 正确参数对于模型的影响
在机器学习模型的训练过程中，参数设定扮演着至关重要的角色。对于cforest算法而言，合理设置参数可以帮助我们提高模型的预测准确性，减少过拟合的风险，并且缩短计算时间。参数的选择能够影响集成中的每棵树的构建方式，树之间的相互关系，以及最终模型对数据的泛化能力。

### 3.1.2 识别关键参数
在众多可调整的参数中，有些参数对于模型性能的影响更大。例如，mtry参数控制了每次分裂时考虑的特征数量，而ntree参数则决定了构建多少棵树。这些核心参数直接关系到模型的构建过程，因此，在模型调优阶段，首先需要识别并重点关注这些参数。

## 3.2 核心参数的调整
### 3.2.1 mtry参数的调整
mtry参数是cforest算法中用于控制随机森林构造时每次分裂尝试的特征数量。在cforest中，这个参数可能更加复杂，因为它与特征抽样的数量息息相关。为了找到最佳的mtry值，通常采用交叉验证的方法来评估不同值对模型预测能力的影响。

以下是使用R语言中的cforest函数调整mtry参数的示例代码：

library(caret)
library(randomForest)

# 设置交叉验证的方法和数据集
control <- trainControl(method="cv", number=10)
mtry_values <- c(2, 3, 4