算法与数据结构：计算机科学基础的基石（附实战案例）：掌握算法与数据结构，夯实计算机科学基础

# 1. 算法与数据结构概述**

算法是解决特定问题的步骤序列，而数据结构是组织和存储数据的有效方式。算法与数据结构是计算机科学的基础，它们共同决定了程序的效率和正确性。

算法的复杂度衡量算法的效率，包括时间复杂度和空间复杂度。时间复杂度表示算法执行所需的时间，而空间复杂度表示算法所需的内存空间。

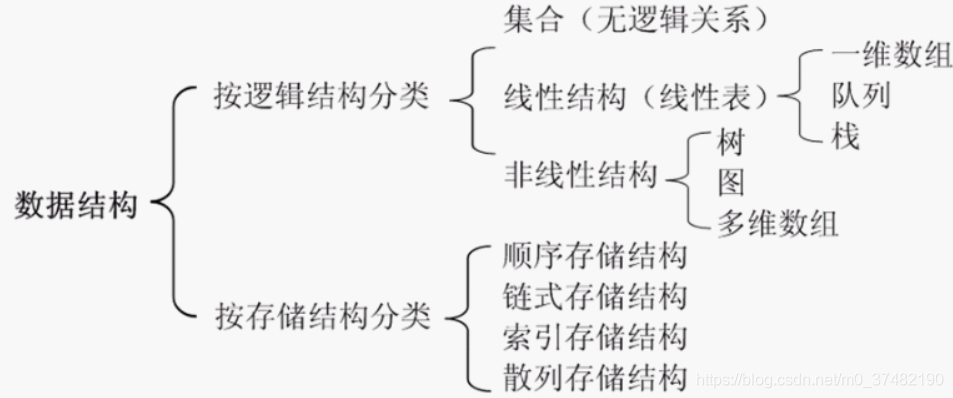
数据结构提供了多种组织和存储数据的方式，包括数组、链表、树和图。每种数据结构都有其独特的优势和劣势，选择合适的数据结构对于优化程序性能至关重要。

# 2.1 算法的复杂度分析

### 2.1.1 时间复杂度

时间复杂度衡量算法执行所需的时间，通常表示为输入规模 n 的函数。常见的时间复杂度类别包括：

- **O(1)**：常数时间，无论输入规模如何，算法执行时间始终相同。
- **O(log n)**：对数时间，算法执行时间随输入规模的增加而对数增长。
- **O(n)**：线性时间，算法执行时间与输入规模成正比增长。
- **O(n^2)**：平方时间，算法执行时间与输入规模的平方成正比增长。
- **O(2^n)**：指数时间，算法执行时间随输入规模的增加呈指数增长。

### 2.1.2 空间复杂度

空间复杂度衡量算法执行所需的内存空间，也表示为输入规模 n 的函数。常见的空间复杂度类别包括：

- **O(1)**：常数空间，无论输入规模如何，算法所需的内存空间始终相同。
- **O(log n)**：对数空间，算法所需的内存空间随输入规模的增加而对数增长。
- **O(n)**：线性空间，算法所需的内存空间与输入规模成正比增长。
- **O(n^2)**：平方空间，算法所需的内存空间与输入规模的平方成正比增长。

### 代码示例

def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

**逻辑分析：**

该代码块实现了一个线性搜索算法。它遍历数组 `arr`，并逐个检查每个元素是否等于目标值 `target`。如果找到目标值，则返回其索引；否则，返回 -1。

**参数说明：**

- `arr`: 要搜索的数组
- `target`: 要查找的目标值

**时间复杂度：**

O(n)，因为算法需要遍历整个数组，其长度为 n。

**空间复杂度：**

O(1)，因为算法不需要额外的内存空间。

### 流程图

graph LR
subgraph 算法复杂度分析
    A[时间复杂度] --> B[空间复杂度]
    B[空间复杂度] --> C[代码示例]
    C[代码示例] --> D[逻辑分析]
    D[逻辑分析] --> E[参数说明]
    E[参数说明] --> F[时间复杂度]
    F[时间复杂度] --> G[空间复杂度]
end

# 3. 数据结构**

**3.1 数组和链表**

**3.1.1 数组的实现和应用**

数组是一种线性数据结构，它存储元素的集合，每个元素都有一个唯一索引。数组在内存中是连续存储的，这意味着元素的访问速度很快。

**实现：**

在大多数编程语言中，数组使用固定大小的连续内存块实现。每个元素都存储在特定索引处，索引从 0 开始。

**应用：**

数组广泛用于存储大量同类型数据，例如：

* 数字数组
* 字符串数组
* 对象数组

**3.1.2 链表的实现和应用**

链表是一种线性数据结构，它由一系列称为节点的元素组成。每个节点包含数据和指向下一个节点的指针。与数组不同，链表中的元素在内存中是不连续存储的。

**实现：**

链表通常使用两个类来实现：`Node` 类和 `LinkedList` 类。`Node` 类存储数据和指向下一个节点的指针，而 `LinkedList`