【HDFS性能提升秘籍】：自定义切片技巧，让数据处理飞跃升级

# 1. HDFS基础与性能挑战

## 1.1 HDFS简介
Hadoop分布式文件系统（HDFS）是Hadoop生态系统的核心组件，它设计用于在廉价的商用硬件上存储大量数据，并提供高吞吐量的数据访问。HDFS具有高容错性，适合于那些有大量数据集的应用程序。HDFS通过将数据分散存储在多个节点上来实现数据冗余，从而保证了即使部分节点失败，数据也不会丢失。

## 1.2 HDFS架构与组件
HDFS的架构由一个NameNode和多个DataNodes组成。NameNode负责管理文件系统的命名空间和客户端对文件的访问；DataNode则在本地文件系统上存储和检索数据块。HDFS对外提供标准的文件系统API，用户可以像操作本地文件系统一样操作HDFS。

## 1.3 性能挑战
尽管HDFS在存储和处理大数据方面表现卓越，但它也面临着性能挑战。由于数据需要被分布在多个节点上，因此网络通信开销成为影响性能的关键因素。另外，数据读写速度和节点故障恢复效率也是影响HDFS性能的重要方面。本章将探索这些挑战以及如何通过优化HDFS配置和策略来应对这些问题。

# 示例：HDFS文件系统命令
hadoop fs -ls / # 列出HDFS根目录下的文件和目录

通过深入分析HDFS的基础知识，读者将为理解后续章节中的数据切片机制、自定义切片技术和性能优化等高级话题打下坚实基础。

# 2. 理解HDFS数据切片机制

### 2.1 HDFS数据切片的基本概念

#### 2.1.1 切片的定义及其在HDFS中的作用

在Hadoop分布式文件系统（HDFS）中，数据切片是一种将大文件分割为小块的过程，每个小块可以独立地进行读取和处理。切片的概念是HDFS设计的核心之一，它允许将数据分布存储在集群的不同节点上，从而实现数据的高可靠性和并行处理能力。

切片在HDFS中扮演着至关重要的角色，具体功能包括：

- **数据分布**：切片保证了文件数据均匀分布在集群中的各个数据节点上，从而平衡了各个节点的工作负载。
- **容错性**：通过将数据复制到多个节点上，HDFS可以保证即使个别节点出现故障，数据也不会丢失。
- **并行处理**：在执行MapReduce任务时，每个切片可以被单独的Map任务处理，这极大地提高了数据处理的并行度和效率。

#### 2.1.2 标准切片策略的工作原理

HDFS的标准切片策略是指Hadoop框架为文件数据自动进行切片的过程。这个过程通常涉及以下几个步骤：

1. **输入文件的解析**：首先，Hadoop会读取输入文件，并将文件内容分割为若干个block。
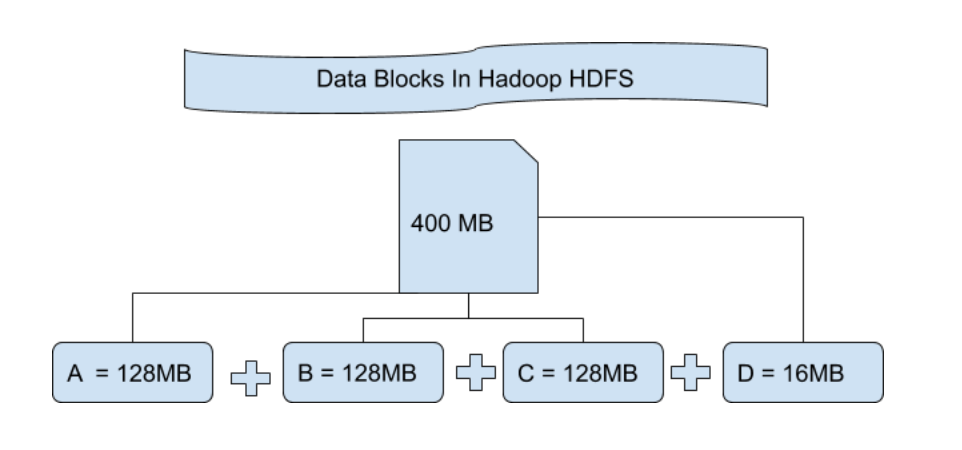
2. **切片大小的决定**：每个block的大小由`dfs.blocksize`参数决定，在Hadoop 2.x版本中，默认大小是128MB。
3. **生成切片**：每个block被视为一个切片，用于Map任务的输入。如果一个文件被切分成多个block，则每个block都会被Map任务独立处理。

### 2.2 切片对性能的影响

#### 2.2.1 数据本地性与网络带宽的权衡

在Hadoop中，数据本地性是一个重要的性能优化因素。数据本地性指的是处理节点与存储数据的节点在同一台机器上或者在同一个网络区域内的程度。

- **本地性优先**：Hadoop优先将任务调度到数据所在节点或邻近节点上，减少网络传输开销，提高数据处理速度。
- **网络带宽**：如果本地性无法保证，数据必须通过网络传输，这时网络带宽就成为了瓶颈。

优化切片策略，需要在数据本地性和网络带宽之间找到平衡点。例如，如果切片设置得太小，虽然可以提高数据本地性，但是会增加任务调度和管理的开销；反之，如果切片太大，虽然任务调度简单，但可能导致网络带宽成为新的瓶颈。

#### 2.2.2 切片大小对MapReduce任务执行的影响

切片大小直接影响MapReduce任务的执行效率：

- **小切片**：可能导致Map任务数量增多，增加了任务的启动和管理开销。每个Map任务处理的数据量较小，可以更快地完成处理，有利于负载均衡。
- **大切片**：减少了Map任务的总数，减少了任务管理开销。但每个Map任务处理的数据量较大，可能会造成处理速度的不均衡，尤其是在处理速度较慢的节点上。

在实际应用中，选择合适的切片大小需要根据数据的特性和集群的资源情况综合考虑。通常，我们需要通过测试和监控来找到最优的切片策略。

在此章节中，我们探讨了HDFS数据切片的基本概念和它对性能影响的深入细节。下一章节，我们将深入解析自定义切片技术的实现原理和策略，以及如何在不同数据类型和大数据集处理场景下应用这些技术。

# 3. 自定义切片技术剖析

在这一章中，我们将深入了解如何通过自定义切片技术来优化Hadoop生态系统中的数据处理任务。本章节将从自定义切片的实现原理出发，逐步探讨如何制定有效的切片策略以及考量因素，并在最后的案例中展示实际应用的效果。

## 3.1 自定义切片的实现原理
### 3.1.1 Hadoop输入格式与切片接口

自定义切片技术是Hadoop输入格式的一个关键特性，它允许开发者根据数据的特定特征和业务需求来调整数据如何被切分成多个片段。Hadoop的输入格式定义了如何将数据源（如文件系统）划分为输入分片（InputSplit），而输入分片是Map任务执行时的单位。自定义输入格式需要实现`InputFormat`接口，并重写`getSplits`方法来指定如何生成分片。

public class CustomInputFormat extends FileInputFormat {
    @Override
    public List<InputSplit> getSplits(JobContext job) throws IOException {
        // 逻辑代码来生成分片列表
    }
}

在上述代码中，`getSplits`方法是定义如何为给定作业生成输入分片的逻辑的核心，其中包括读取配置信息、确定分片边界和计算分片大小等。

### 3.1.2 自定义切片的关键代码实现

关键在于如何在`getSplits`方法中实现自定义逻辑，这通常涉及对数据集的分析和对任务需求的了解。下面是一个简单的例子，展示了如何根据文件大小和预定义的分片大小来创建分片。

List<InputSplit> splits = new ArrayList<>();
Configuration conf = job.getConfiguration();
long targetSize = conf.getLong("mapreduce.input.fileinputformat.split.minsize", 1) * 1024 * 1024;
Path[] files = listStatus(job).getFiles();
for (Path *** {
    long length = file.getFileSystem(conf).getContentSummary(file).getLength();
    if (length >