【机器学习应用案例】：Matlab实现ADNI数据分析的入门与进阶


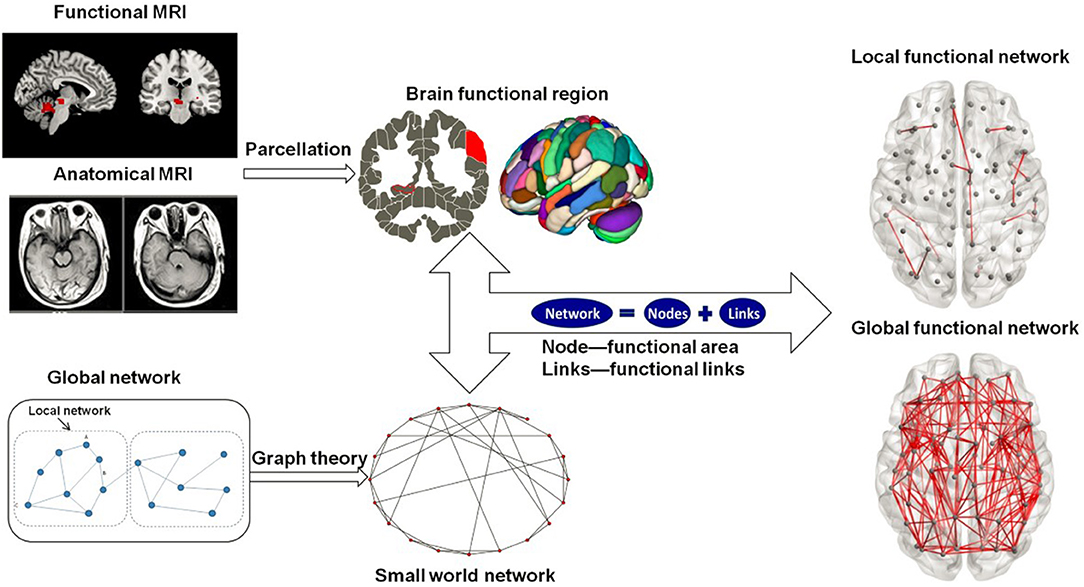
# 摘要
随着ADNI研究的深入，对数据分析的要求日益增高，Matlab作为强大的科学计算软件，已被广泛应用在ADNI数据分析的各个阶段。本文首先介绍了ADNI数据分析的基本概念和Matlab编程基础，接着详细探讨了Matlab数据分析工具箱在数据导入、预处理、探索性分析以及特征工程等关键步骤的应用。随后，文章深入分析了基于Matlab构建统计模型和实现机器学习算法的过程，强调了结果解释与临床意义的重要性。此外，本文还深入讨论了复杂数据处理、高级机器学习方法的应用，以及结果验证与模型部署的策略。最后，通过ADNI数据的案例研究，本文总结了当前机器学习在该领域的应用趋势，并对未来的发展方向和潜在影响进行了展望。

# 关键字
ADNI数据分析；Matlab工具箱；统计模型；机器学习；数据可视化；模型部署

参考资源链接：[ADNI rs-fMRI数据预处理步骤详解](https://wenku.csdn.net/doc/890obger50?spm=1055.2635.3001.10343)
# 1. ADNI数据分析简介与Matlab基础

## 1.1 ADNI数据的背景与重要性
阿尔茨海默病神经成像计划（ADNI）是一个多机构合作的大型项目，旨在通过成像、生物标记、临床和遗传数据的综合分析，加深对阿尔茨海默病（AD）的理解。这些数据对于生物统计学、生物信息学和计算神经科学等领域的研究至关重要，因为它们能够为疾病的发展和治疗提供宝贵的信息。

## 1.2 Matlab在数据分析中的角色
Matlab作为一种高级数学计算和可视化软件，提供了一套完整的工具箱，适用于处理、分析和可视ADNI数据集。它的编程环境简洁易用，特别适合于算法开发、数据处理和统计分析。Matlab的一些内置函数和工具箱支持复杂的数据操作和分析过程，极大地简化了研究者的分析流程。

## 1.3 Matlab的基础知识和功能概述
为了有效地使用Matlab进行数据分析，研究者需要掌握其基础语法、数据类型和控制结构。Matlab的核心数据类型是矩阵，它提供了强大的矩阵运算功能，从而在数值计算方面非常高效。同时，Matlab提供了丰富的统计和机器学习工具箱，这些工具箱包含了大量的函数和类，能够帮助研究者完成从数据导入到模型建立的整个分析过程。

在实际操作中，研究者首先需要熟悉Matlab的环境设置，例如路径配置和工作目录管理，这样才能确保代码的正确执行和结果的准确读取。其次，需要了解如何使用Matlab的内置函数进行基本的数据操作，例如数据导入、类型转换和矩阵操作等。最后，需要掌握如何利用Matlab的数据可视化工具展示分析结果，比如使用plot、histogram等函数绘制图形。通过这些步骤，研究者可以开始他们的数据分析之旅，深入探索ADNI数据集，并逐步构建和验证统计模型。

# 2. Matlab数据分析工具箱的应用

## 2.1 数据导入与预处理
在处理ADNI数据集时，数据的导入与预处理是至关重要的第一步，因为它直接影响到后续分析的质量和可信度。Matlab提供了一系列内置函数和工具箱来简化这一过程。

### 2.1.1 使用Matlab导入ADNI数据集
Matlab支持多种数据格式的导入，包括CSV, Excel, JSON等。对于ADNI数据集，通常包含大量的时间序列数据和神经成像数据。在此，我们以CSV格式为例，展示如何导入数据：

% 假设数据集文件名为 "adni_data.csv"
data = csvread('adni_data.csv');

% 查看数据的维度
size(data)

以上代码执行后，将返回数据集的行数和列数。Matlab还提供`readtable`函数来导入数据，该函数返回的数据类型为table，提供了更丰富的数据操作选项。

### 2.1.2 数据清洗与格式转换
导入数据之后，经常需要对数据进行清洗和格式转换，以确保数据的准确性和完整性。以下是一些常见的数据清洗步骤：

% 假设data为导入的矩阵形式的数据集
% 删除缺失值
clean_data = rmmissing(data);

% 将数据转换为table格式，以便于后续操作
clean_data_table = array2table(clean_data, 'VariableNames', varNames);

% 格式转换，例如，将字符串转换为数值型数据
clean_data_table.numVar = str2double(clean_data_table.numVar);

在上述代码中，`rmmissing`用于删除包含缺失值的数据行，`array2table`用于将矩阵数据转换为table类型，而`str2double`函数将字符串转换为双精度数值。

## 2.2 数据探索性分析
在数据导入和预处理之后，进行探索性分析是理解数据特征和分布的重要环节。

### 2.2.1 描述性统计分析
Matlab提供了丰富的统计函数来实现描述性统计分析，如`mean`, `median`, `std`, `var`等。

% 计算数据集的平均值、中位数、标准差和方差
meanValue = mean(clean_data_table.numVar);
medianValue = median(clean_data_table.numVar);
stdValue = std(clean_data_table.numVar);
varValue = var(clean_data_table.numVar);

% 输出结果
disp(['Mean: ', num2str(meanValue)]);
disp(['Median: ', num2str(medianValue)]);
disp(['Standard Deviation: ', num2str(stdValue)]);
disp(['Variance: ', num2str(varValue)]);

上述代码计算了数据集中`numVar`列的均值、中位数、标准差和方差，并打印出来。

### 2.2.2 数据可视化技术
Matlab同样提供了强大的绘图功能，可以帮助用户以图形化的方式探索数据。

% 绘制直方图
figure;
histogram(clean_data_table.numVar);
title('Histogram of numeric variable');
xlabel('Value');
ylabel('Frequency');

% 绘制箱型图
figure;
boxplot(clean_data_table.numVar);
title('Boxplot of numeric variable');
xlabel('Variable');
ylabel('Value');

上述代码块使用`histogram`和`boxplot`函数分别绘制了`numVar`变量的直方图和箱型图，方便我们观察数据的分布和离群点。

## 2.3 特征工程与选择
特征工程是数据分析中的关键步骤，涉及从原始数据中提取和构造出更有意义的特征。

### 2.3.1 特征提取方法
在Matlab中，特征提取可以通过线性变换、非线性变换以及使用预训练模型等方法实现。

% 使用主成分分析（PCA）提取特征
[coeff, score, latent] = pca(clean_data_table);

% 选择保留的主成分数量
numComponents = 5;
reducedData = score(:, 1:numComponents);

% 将提取后的特征保存到新的table中
reducedDataTable = array2table(reducedData, 'VariableNames', sprintf('PC%d', 1:numComponents));

以上代码运用PCA算法来提取主要的特征成分，并只保留前5个主成分。

### 2.3.2 特征选择策略
特征选择的目的是减少特征数量，避免过拟合，并提高模型的泛化能力。

% 假设我们的目标变量为targetVar
% 使用回归模型选择特征
selectedFeatures = stepwiselm(clean_data_table, 'linear', 'ResponseVar', 'targetVar', 'PEnter', 0.05);

% 输出被选择的特征
selectedVars = selectedFeatures.Coefficients.Variable;
disp(selectedVars);

上述代码使用逐步线性回归模型选择特征，其中`PEnter`参数控制了新特征进入模型的显著性水平。

通过以上分析，我们完成了Matlab数据分析工具箱在ADNI数据集导入、预处理、探索性分析、特征提取和选择的应用。接下来，我们将深入讨论如何利用Matlab进行统计分析。

# 3. Matlab在ADNI数据的统计分析中应用

## 3.1 基于