【单纯形法的稳定性问题】:确保数值稳定性的重要性


单纯形法代码
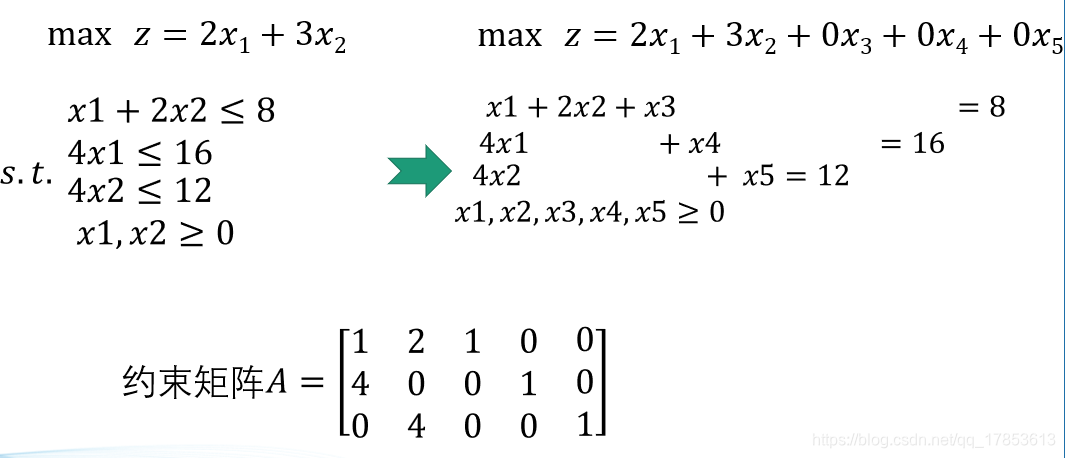
摘要
本文系统性地探讨了单纯形法在数学优化领域的基础理论、实现方法及其优化策略。首先,介绍了单纯形法的标准算法及其关键步骤,并详细分析了算法在数值稳定性方面的问题及其对结果的影响。针对稳定性问题,提出了有效的改进策略,包括数值校正和高精度计算技术,并通过一系列测试方法论和实验结果进行了评估。文章进一步探讨了单纯形法在编程实现与稳定性保障方面的工程实践,强调了单元测试与代码审查的重要性。最后,本文通过分析经济学和工程领域的应用案例,展示了单纯形法的实际应用价值,并对其未来发展趋势和挑战进行了展望。
关键字
单纯形法;数值稳定性;算法优化;编程实现;应用案例;未来趋势
参考资源链接:Python实现单纯形法:原理、代码与优化解求解
1. 单纯形法的基础理论
简介
单纯形法是数学优化领域中解决线性规划问题的一种基本算法。其核心在于在多维空间中寻找一个最优的角点,这个角点代表了线性规划问题的一个最优解。
理论基础
线性规划问题通常表述为在一组线性不等式约束下,求解目标函数的最大值或最小值。单纯形法的理论基础是线性代数中的单纯形概念以及凸多面体顶点的性质。
算法原理
单纯形法通过迭代寻找最优的角点,每一次迭代都将改善目标函数的值,直至找到最优解或确定问题无界或无解。这一过程涉及到基变量与非基变量的交换,以及在可行解空间中沿着边进行移动。
在单纯形法中,线性规划问题首先需要被转化为标准形式,接着通过基本可行解开始迭代。每次迭代中,都会选取进入基的变量和离开基的变量,以最小化目标函数的损失。
接下来章节会详细探讨单纯形法的实现与优化方式,以及如何处理算法中出现的数值稳定性问题,保证结果的精确性和算法的高效性。
2. 单纯形法的实现与优化
2.1 单纯形法的标准算法
2.1.1 算法流程概述
单纯形法是解决线性规划问题的一种高效算法,由George Dantzig在1947年提出。它特别适用于求解标准形式的线性规划问题。单纯形法的基本思想是通过在可行域的顶点之间移动,寻找使目标函数达到最优值的解。算法从一个基本可行解开始,通过迭代移动到相邻的顶点,直到找到最优解或者证明问题无界或无解。
标准的单纯形法算法流程如下:
- 将线性规划问题转换为标准形式。
- 寻找初始基本可行解(可能需要使用辅助问题)。
- 确定进入基变量和离开基变量。
- 进行单纯形迭代,更新基变量。
- 检查是否达到最优性,如果满足最优性条件则停止迭代。
- 如果存在进入基的变量,则选择一个进行迭代;如果不存在,问题的最优解已经找到。
2.1.2 关键步骤详解
寻找初始基本可行解:
初始基本可行解是单纯形算法的起点,通常可以使用大M方法或两阶段法来获得。如果线性规划问题直接有基本可行解,则可以直接进行下一步。
确定进入基变量和离开基变量:
在每一步迭代中,算法需要确定一个进入基的变量和一个离开基的变量。这需要进行以下计算:
- 进入基变量:计算目标函数系数的负值,如果所有系数都是非负的,则当前解为最优解。
- 离开基变量:根据最小比率测试确定哪个基变量离开。
单纯形迭代:
在确定了进入和离开变量后,进行基矩阵的更新,这通常涉及线性代数操作,如高斯消元法。
最优性检查:
在每次迭代后,需要检查是否满足最优性条件,即所有非基变量的目标函数系数非负。如果满足,当前解是最优解。
- # 示例:单纯形法伪代码
- def simplex_method(A, b, c):
- # A, b, c 分别是线性规划问题的系数矩阵、约束向量和目标函数系数向量
- while not optimal:
- entering_var = select_entering_variable(c, A)
- leaving_var = select_leaving_variable(A, b)
- if not leaving_var:
- optimal = True
- else:
- pivot(A, b, entering_var, leaving_var)
- return current_solution
- # 选择进入基变量
- def select_entering_variable(c, A):
- # 逻辑分析:选择目标函数中系数最小的非基变量作为进入变量
- # 参数说明:c为目标函数系数向量,A为系数矩阵
- # 返回选择的变量索引
- pass
- # 选择离开基变量
- def select_leaving_variable(A, b):
- # 逻辑分析:通过最小比率测试选择离开的变量
- # 参数说明:A为系数矩阵,b为约束向量
- # 返回选择的变量索引
- pass
- # 主循环迭代
- def pivot(A, b, entering_var, leaving_var):
- # 逻辑分析:执行基本单纯形法的主循环
- # 参数说明:A为系数矩阵,b为约束向量
- # 具体的旋转操作
- pass
- # 检查最优性
- def check_optimality(c, A):
- # 逻辑分析:判断是否达到最优解
- # 参数说明:c为目标函数系数向量,A为系数矩阵
- # 返回布尔值,表示是否最优
- pass
以上为单纯形法关键步骤的伪代码实现和逻辑分析。在实际应用中,需对这些步骤进行具体的编程实现,并针对具体问题进行算法优化。
2.2 算法中的数值稳定性问题
2.2.1 稳定性问题的来源
单纯形法在实际计算过程中可能会遇到数值稳定性问题,这些问题主要源自于以下几个方面:
- 舍入误差:计算机在进行浮点运算时,由于无法精确表示所有实数,会产生舍入误差。
- 数值计算方法:算法中涉及到的线性代数运算,如矩阵求逆,可能会因为数值方法的局限性而引起误差积累。
- 数据问题:输入数据的不精确性,如测量误差、数据的离散性等,也会造成算法运行过程中的不稳定性。
2.2.2 稳定性对结果的影响
数值稳定性问题会影响到单纯形法的计算结果,主要表现在以下几个方面:
- 最优性判断错误:稳定性问题可能导致算法错误地认为已经找到了最优解,从而停止迭代。
- 目标函数值计算误差:数值不稳定可能会导致目标函数值计算不准确,影响到决策的可靠性。
- 算法迭代次数增加:由于数值问题导致无法准确地进行最优性判断和变量替换,算法可能需要更多的迭代才能找到最优解,甚至陷入循环。
2.3 稳定性改进策略
2.3.1 数值校正方法
为了解决数值稳定性问题,首先可以采用
































