MATLAB函数句柄在数值分析中的应用：优化和求解方程，加速计算进程

# 1. MATLAB函数句柄概述**

MATLAB函数句柄是一种特殊类型的变量，它指向MATLAB函数。函数句柄允许我们将函数作为参数传递给其他函数，从而实现函数的动态调用和操作。

函数句柄的语法为`@函数名`，其中`函数名`是MATLAB函数的名称。例如，`@sin`指向MATLAB中的`sin`函数。

函数句柄具有以下特性：

- **可调用性：**函数句柄可以像普通函数一样被调用，例如`f = @sin; y = f(x);`。
- **可传递性：**函数句柄可以作为参数传递给其他函数，例如`plot(@sin, x)`。
- **可存储性：**函数句柄可以存储在变量中，例如`my_func = @sin;`。

# 2. 函数句柄在优化中的应用

### 2.1 优化问题的数学基础

优化问题是寻找一个函数在给定约束条件下的最小值或最大值的问题。数学上，优化问题可以表示为：

min/max f(x)
subject to:
g(x) <= 0, h(x) = 0

其中：

* `f(x)` 是目标函数，需要最小化或最大化。
* `g(x)` 是不等式约束条件。
* `h(x)` 是等式约束条件。

### 2.2 函数句柄在优化算法中的使用

函数句柄是一种在 MATLAB 中表示函数的方法。它允许将函数作为参数传递给其他函数，从而实现算法的模块化和可重用性。在优化算法中，函数句柄主要用于定义目标函数和约束条件。

#### 2.2.1 梯度下降法

梯度下降法是一种迭代优化算法，用于寻找函数的局部最小值。它通过沿着目标函数梯度的负方向更新当前点，逐步逼近最小值。

function [x, fval] = gradient_descent(f, x0, alpha, max_iter)
    % 输入：
    %   f: 目标函数的函数句柄
    %   x0: 初始点
    %   alpha: 学习率
    %   max_iter: 最大迭代次数
    % 输出：
    %   x: 最优解
    %   fval: 最优值
    x = x0;
    for i = 1:max_iter
        grad = gradient(f, x);  % 计算目标函数的梯度
        x = x - alpha * grad;  % 更新当前点
    end
    fval = f(x);
end

**代码逻辑分析：**

* `gradient_descent` 函数接受目标函数句柄 `f`、初始点 `x0`、学习率 `alpha` 和最大迭代次数 `max_iter` 作为输入。
* 函数使用梯度下降算法迭代更新当前点 `x`，直到达到最大迭代次数。
* 在每次迭代中，函数计算目标函数 `f` 在当前点 `x` 的梯度 `grad`，并沿着梯度的负方向更新 `x`。
* 函数返回最优解 `x` 和最优值 `fval`。

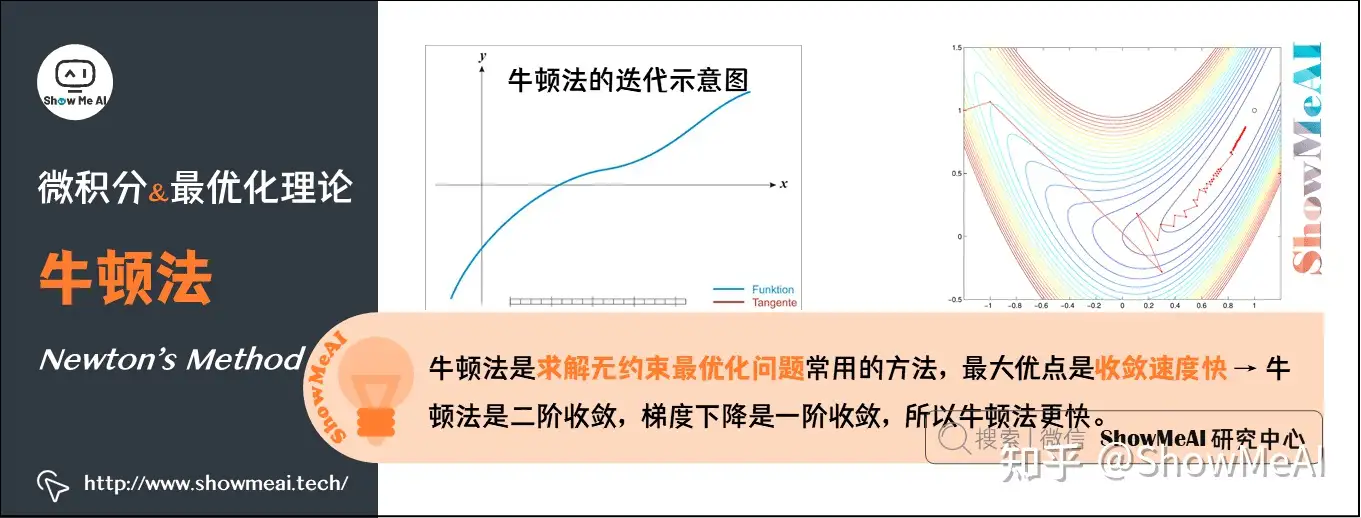
#### 2.2.2 牛顿法

牛顿法是一种二阶优化算法，用于寻找函数的局部最小值。它通过使用目标函数的二阶导数信息来更新当前点，比梯度下降法收敛得更快。

function [x, fval] = newton_method(f, x0, max_iter)
    % 输入：
    %   f: 目标函数的函数句柄
    %   x0: 初始点
    %   max_iter: 最大迭代次数
    % 输出：
    %   x: 最优解
    %   fval: 最优值
    x = x0;
    for i = 1:max_iter
        grad = gradient(f, x);  % 计算目标函数的梯度
        hessian = hessian(f, x);  % 计算目标函数的二阶导数
        x = x - hessian \ grad;  % 更新当前点
    end
    fval = f(x);
end

**代码逻辑分析：**

* `newton_method` 函数接受目标函数句柄 `f`、初始点 `x0` 和最大迭代次数 `max_iter` 作为输入。
* 函数使用牛顿法迭代更新当前点 `x`，直到达到最大迭代次数。
* 在每次迭代中，函数计算目标函数 `f` 在当前点 `x` 的梯度 `grad` 和二阶导数 `hessian`，并使用牛顿更新公式更新 `x`。
* 函数返回最优解 `x` 和最优值 `fval`。

#### 2.2.3 共轭梯度法

共轭梯度法是一种迭代优化算法，用于解决大规模线性方程组和优化问题。它通过构造一组共轭方向来加速收敛。

function [x, fval] = conjugate_gradient(f, x0, max_iter)
    % 输入：
    %   f: 目标函数的函数句柄
    %   x0: 初始点
    %   max_iter: 最大迭代次数
    % 输出：
    %   x: 最优解
    %   fval: 最优值
    x = x0;
    r = gradient(f, x);  % 计算目标函数的梯度
    p = -r;  % 设置初始搜索方向
    for i = 1:max_iter
        alpha = r' * r / (p' * hessian(f, x) * p);  % 计算步长
        x = x + alpha * p;  % 更新当前点
        r_new = gradient(f, x);  % 计算新的梯度
        beta = r_new' * r_new / (r' * r);  % 计算共轭参数
        p = -r_new + beta * p;  % 更新搜索方向
        r = r_new;
    end
    fval = f(x);
end

**代码逻辑分析：**

* `conjugate_gradient` 函数接受目标函数句柄 `f`、初始点 `x0` 和最大迭代次数 `max_iter` 作为输入。
* 函数使用共轭梯度法迭代更新当前点 `x`，直到达到最大迭代次数。
* 在每次迭代中，函数计算目标函数 `f` 在当前点 `x` 的梯度 `r`，并使用共轭梯度更新公式更新搜索方向 `p`。
* 函数返回最优解 `x` 和最优值 `fval`。

# 3. 函数句柄在求解方程中的应用**

### 3.1 非线性方程求解的基本原理

非线性方程是指形式为 f(x) = 0 的方程，其中 f(x) 是非线性的函数。与线性方程不同，非线性方程的求解通常需要使用迭代方法。

迭代方法的基本思想是：从一个初始猜测值 x0 开始，通过迭代公式 x(n+1) = g(x(n)) 逐步逼近方程的根。其中，g(x) 是一个收缩映射，即对于任何 x1 和 x2，都有 |g(x1) - g(x2)| < |x1 - x2|。

常用的迭代方法包括：

- 固定点迭代法：g(x) = f(x)
- 拟牛顿法：g(x) = x - H(x)f(x)，其中 H(x) 是近似海森矩阵的正定矩阵
- 信赖域法：在 f(x) 在 x 附近的一定区域内近似为二次函数，然后求解二次函数的极小值点作为下一次迭代点

### 3.2 函数句柄在求解非线性方程中的使用

MATLAB 中可以使用函数句柄来表示非线性方程 f(x) = 0。这使得求解非线性方程变得更加方便和灵活。

下面是一个使用函数句柄求解非线性方程的示例：

% 定义非线性方程
f = @(x) x^3 - 2*x + 1;

% 初始猜测值
x0 = 1;

% 设置迭代次数和容差
max_iter = 100;
tol = 1e-6;

% 迭代求解
for i = 1:max_iter
    % 计算下一轮迭代点
    x1 = x0 - f(x0)/fdiff(f, x0);
    % 检查是否收敛
    if abs(x1 - x0) < tol
        break;
    end
    % 更新迭代点
    x0 = x1;
end

% 输出求解结果
fprintf('根为：%.6f\n', x1);

在该示例中，函数句柄 f 表示非线性方程 f(x) = 0。迭代公式 x(n+1) = x(n) - f(x(n))/fdiff(f, x(n)) 使用了 MATLAB 的 fdiff 函数来计算 f(x) 的导数。

### 3.2.1 固定点迭代法

固定点迭代法是求解非线性方程最简单的方法。其迭代公式为：

x(n+1) = f(x(n))

该方法的收敛条件是：

|f'(x)| < 1

对于收敛区域内的初始猜测值，固定点迭代法可以快速收敛到方程的根。

### 3.2.2 拟牛顿法

拟牛顿法是一种二阶收敛方法，其迭代公式为：

x(n+1) = x(n) - H(x(n))f(x(n))

其中，H(x) 是近似海森矩阵的正定矩阵。拟牛顿法在收敛速度上优于固定点迭代法，但需要计算海森矩阵的近似值，计算量较大。

### 3.2.3 信赖域法

信赖域法是一种收敛速度较快的迭代方法，其基本思想是在 f(x) 在 x 附近的一定区域内近似为二次函数，然后求解二次函数的极小值点作为下一次迭代点。

信赖域法的迭代公式为：

x(n+1) = x(n) + arg min{f(x) + (1/2)(x - x(n))^T H(x(n))(x - x(n))}

其中，H(x) 是海森矩阵的近似值。信赖域法在收敛速度和计算量之间取得了较好的平衡。

# 4. 函数句柄在加速计算进程中的应用**

**4.1 并行计算的基本概念**

并行计算是一种利用多核处理器或分布式系统同时执行多个任务的技术，以提高计算速度和效率。并行计算的基本概念包括：

* **多核处理器：**一个计算机芯片上包含多个处理器内核，每个内核可以独立执行任务。
* **分布式系统：**多个计算机或节点通过网络连接，共同执行任务。
* **并行算法：**专门设计用于在并行系统上运行的算法，可以将任务分解成多个并行执行的部分。

**4.2 函数句柄在并行计算中的使用**

函数句柄可以在并行计算中发挥重要作用，因为它允许在不同的处理器或节点上同时执行函数。

**4.2.1 多核并行**

在多核处理器上，可以使用并行编程库（如 OpenMP）将函数句柄传递给并行区域，从而在不同的内核上同时执行函数。例如：

% 创建一个函数句柄
f = @(x) x^2;

% 使用 OpenMP 将函数句柄传递给并行区域
parallel for i = 1:1000000
    result(i) = f(i);
end

在这个示例中，`f` 函数句柄被传递给并行 `for` 循环，该循环将在不同的内核上并行计算 `result` 数组中的元素。

**4.2.2 分布式并行**

在分布式系统上，可以使用消息传递接口（如 MPI）将函数句柄传递给不同的节点，从而在不同的计算机上同时执行函数。例如：

% 创建一个函数句柄
f = @(x) x^2;

% 使用 MPI 将函数句柄发送给不同的节点
my_rank = MPI_Comm_rank(MPI_COMM_WORLD);
if my_rank == 0
    % 根节点发送函数句柄给其他节点
    for i = 1:num_nodes
        MPI_Send(f, 1, MPI_OBJECT_C, i, 0, MPI_COMM_WORLD);
    end
else
    % 其他节点接收函数句柄
    MPI_Recv(f, 1, MPI_OBJECT_C, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
end

% 在每个节点上执行函数
result = f(1000000);

% 根节点收集结果
if my_rank == 0
    for i = 1:num_nodes
        MPI_Recv(result_partial, 1, MPI_DOUBLE, i, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
        result = result + result_partial;
    end
end

在这个示例中，根节点使用 MPI 将 `f` 函数句柄发送给其他节点。然后，每个节点使用函数句柄计算结果，并将其发送回根节点。根节点收集所有结果并计算总和。

通过使用函数句柄，可以在并行计算中轻松地分发和执行函数，从而显著提高计算速度和效率。

# 5.1 函数句柄在积分和微分中的应用

函数句柄在数值分析中另一个重要的应用是积分和微分。在 MATLAB 中，可以使用 `integral` 和 `diff` 函数来计算积分和微分。

### 积分

`integral` 函数的语法如下：

integral(fun, lower, upper, options)

其中：

* `fun` 是一个函数句柄，表示被积函数。
* `lower` 和 `upper` 是积分的下限和上限。
* `options` 是一个可选参数，用于指定积分方法和其他选项。

例如，计算函数 `f(x) = x^2` 在区间 [0, 1] 上的积分：

fun = @(x) x.^2;
integral(fun, 0, 1)

输出结果：

0.3333

### 微分

`diff` 函数的语法如下：

diff(y, x, n)

其中：

* `y` 是一个向量或矩阵，表示要计算微分的函数值。
* `x` 是一个向量或矩阵，表示函数的自变量值。
* `n` 是一个可选参数，指定微分的阶数（默认为 1）。

例如，计算函数 `f(x) = x^2` 在点 `x = 1` 处的导数：

fun = @(x) x.^2;
diff(fun(1))

输出结果：

2